Theoretischer Hintergrund
Die Schwingungsbewegung eines zunächst ungestörten, dann harmonisch angeregten mechanischen Systems besteht aus einer gedämpften Eigenschwingung mit abnehmender Amplitude und einer erzwungenen Schwingung mit konstanter Amplitude. Einschwingvorgang und eingeschwungener Zustand werden in folgender Formel beschrieben.
| t | Zeit |
| ω | Erregerkreisfrequenz |
| ωD | Eigenkreisfrequenz |
| ζ | Dämpfung |
| A | Konstante |
| B | Konstante |
| C | Konstante |
| D | Konstante |
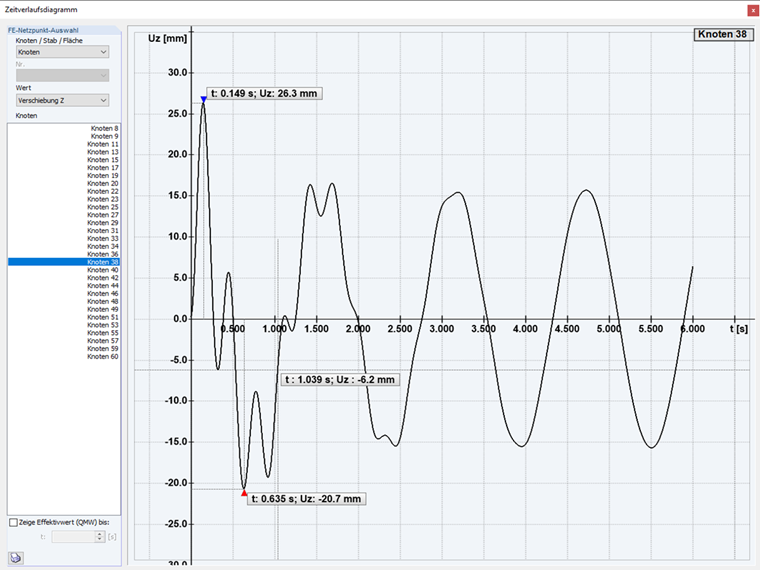
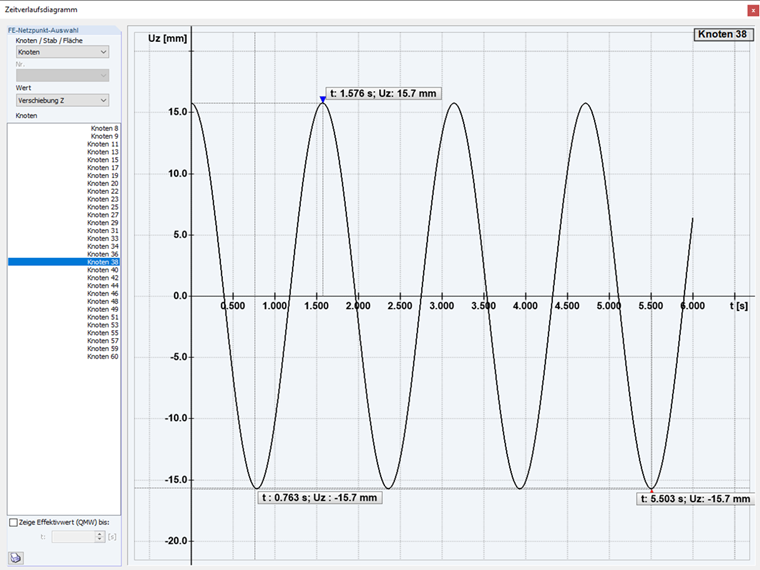
Ist dieses Frequenzverhältnis η < 1, man spricht dann von unterkritischer Anregung, so verläuft die erzwungene Schwingung langsamer als die gedämpfte Eigenschwingung und es entsteht ein Einschwingvorgang. Das System schwingt sich nach einigen schnellen Perioden der gedämpften Eigenschwingung auf die langsamere, erzwungene Schwingung ein, die schließlich als einziger Schwingungsanteil verbleibt.
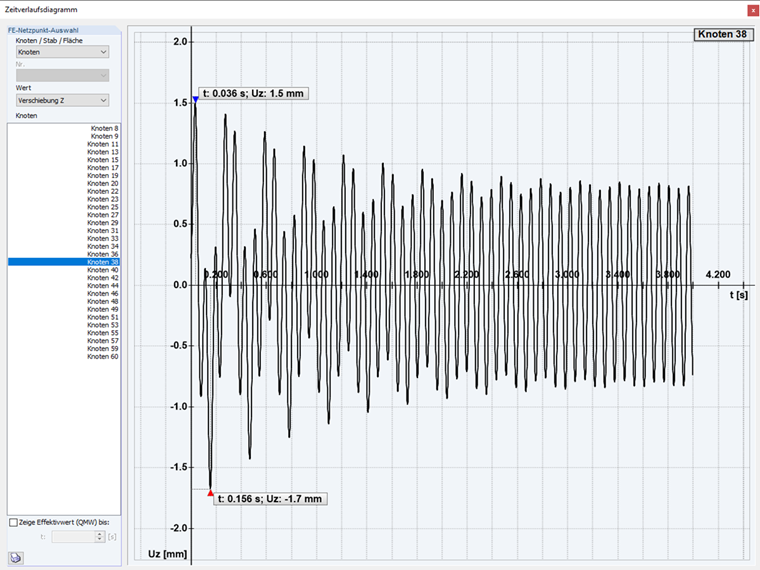
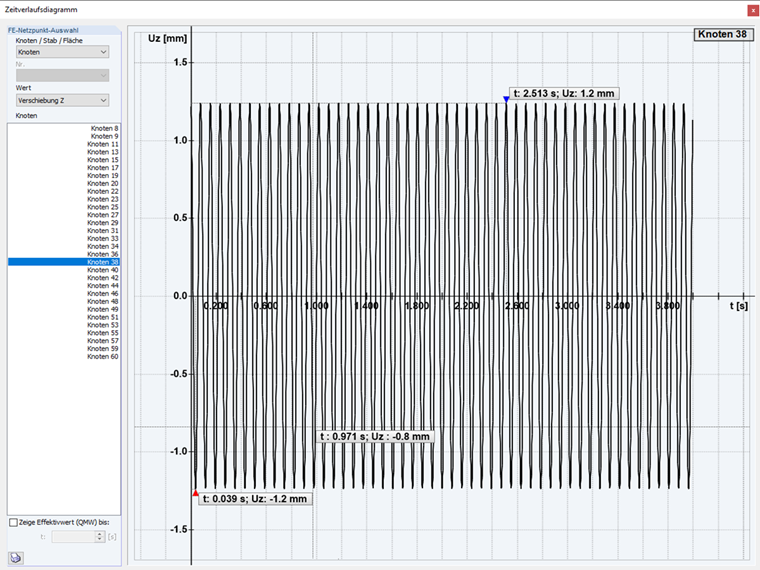
Liegt der Fall η > 1 vor, jetzt überkritische Anregung genannt, dann ist die erzwungene Schwingung in der Frequenz höher als die gedämpfte Eigenschwingung. Nun findet eine schnelle harmonische Schwingung um die langsamere, gedämpfte Eigenschwingung statt, bis diese vollständig abgeklungen ist und wiederum nur der durch die Anregung erzwungene Schwingungsanteil übrigbleibt.
Da in allen praktisch vorkommenden Fällen Dämpfung vorhanden ist, die zum Abklingen der Eigenschwingung führt, ist es unabhängig vom Frequenzverhältnis ausschließlich von Interesse, die jeweils nur verbleibende erzwungene Schwingungsbewegung (stationärer Teil) zu betrachten und weiter zu analysieren. Diese Schwingungsbewegung wird als (quasi-)stationäre Schwingung bezeichnet und der zugehörige Zustand des Systems eingeschwungener Zustand genannt.
Die Eigenschwingung hat die Kreisfrequenz ωD des gedämpften Systems, während der durch die Anregung erzwungene Schwingungsanteil die Kreisfrequenz ω der harmonischen Anregung besitzt. Die Gesamtschwingung, die sich aus der Überlagerung dieser beiden Teilschwingungen ergibt, nimmt daher einen Verlauf, dessen Erscheinungsbild stark vom Verhältnis ω/ωD, also vom Frequenzverhältnis η, abhängt.
Beispiel
Nachfolgend wird das Verhalten des Einschwingens anhand einer Stahl-Struktur erläutert. Angenommen wird, dass diese Struktur harmonisch erregt wird. Dafür werden in der Struktur harmonische Erregungen erzeugt, um die verschiedenen Einschwingvorgänge aufzuzeigen. Um die Frequenz der harmonischen Erregung besser auf die Struktur abzustimmen, wird mittels DYNAM Pro - Eigenschwingungen zunächst ein Eigenschwingungsfall erzeugt. Als Vereinfachung werden in den Eigenschwingungsfällen nur Eigenformen in globale Z-Richtung betrachtet.
Unterkritische Erregung: Im ersten Fall des Zeitverlaufsverfahrens wird eine sogenannte unterkritische Erregung der Struktur durchgeführt. Mit einer Erregerfrequenz kleiner der Eigenform.
Überkritische Erregung: Im zweiten Fall des Zeitverlaufsverfahrens wird eine sogenannte überkritische Erregung der Struktur durchgeführt. Mit einer Erregerfrequenz größer der Eigenform.
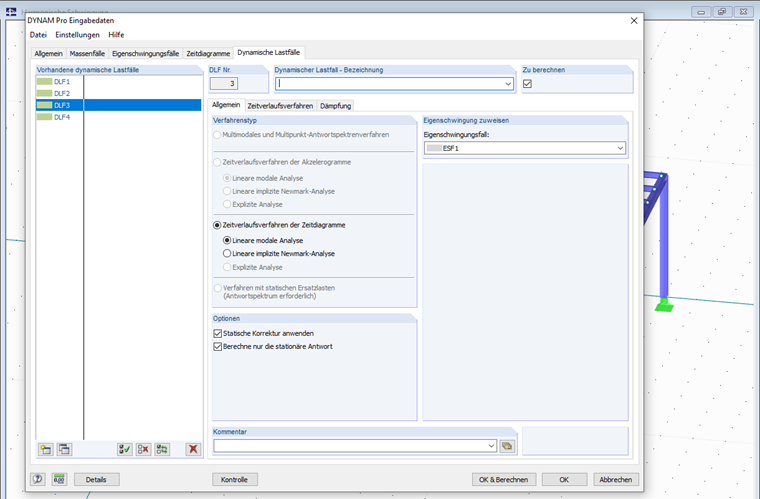
Im dritten und vierten Fall wird in DYNAM Pro - Erzwungene Schwingungen die Möglichkeit der stationären Lösung für beide zuvor erstellten Erregerfälle genutzt. Dabei stellt sich direkt der stationäre Zustand ein. Dieser wird allgemeinen auch als eingeschwungener Zustand beschrieben.
_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)
_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)
_LI.jpg?mw=350&hash=3d52d6017982f88052836929c5d9b0ba0ab8104f)
