Voltar para a base de dados de conhecimento

13498x

001705

M.Eng. Milan Gérard

2021-02-05

Cálculo de pilares de betão sujeitos a flexão combinada com o RF-CONCRETE Columns

O presente artigo trata de elementos cuja secção está sujeita, simultaneamente, a um momento fletor, uma força de corte e uma força axial de compressão ou tração. No entanto, no nosso exemplo não iremos incluir o carregamento devido à força de corte.

O que é a flexão combinada?

A flexão combinada é designada pelo sistema (M_G0, N) aplicado num ponto C, designado por centro de pressão. A distância G₀ C é designada por excentricidade da força externa em relação ao centro de gravidade G₀ da secção de betão puro.

Na flexão combinada, o valor do momento fletor depende apenas deste ponto, onde é realizada a redução das forças; aqui, é G₀.

e_{0} = \frac{M_{{EdG}_{0}}}{N_{Ed}}

e₀	Excentricidade em relação ao centro de gravidade de uma secção de betão puro
M_EdG0	Valor de cálculo do momento fletor em relação ao centro de gravidade de uma secção de betão puro
N_Ed	Valor de cálculo da força axial atuante

Excentricidade em relação ao centro de gravidade da secção de betão puro

A primeira coisa a fazer na flexão combinada é encontrar a posição do centro de pressão calculando e₀.

Consideração de imperfeições geométricas e efeitos de segunda ordem em U'

A análise de elementos e estruturas deve ter em consideração os efeitos desfavoráveis de quaisquer imperfeições geométricas na estrutura, bem como os desvios na posição das cargas. Os desvios nas dimensões das secções' são normalmente considerados pelos coeficientes parciais de segurança para os materiais.

Esbelteza e comprimento efetivo de elementos isolados

λ = \frac{l_{0}}{i}

l_{0} = β \cdot l

λ	Coeficiente de esbelteza
l₀	Comprimento efetivo determinado
i	Raio de giração da secção de betão não fendilhada
β	Coeficiente do comprimento de encurvadura
l	Comprimento livre

coeficiente de esbelteza

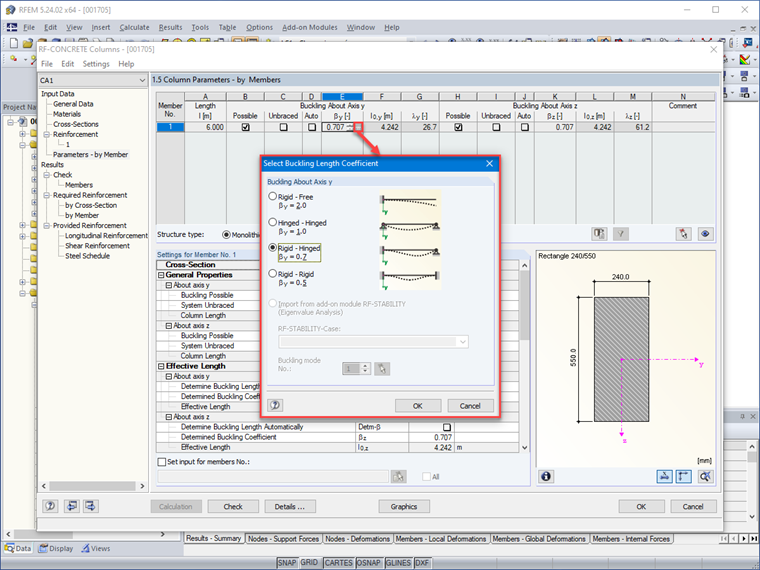
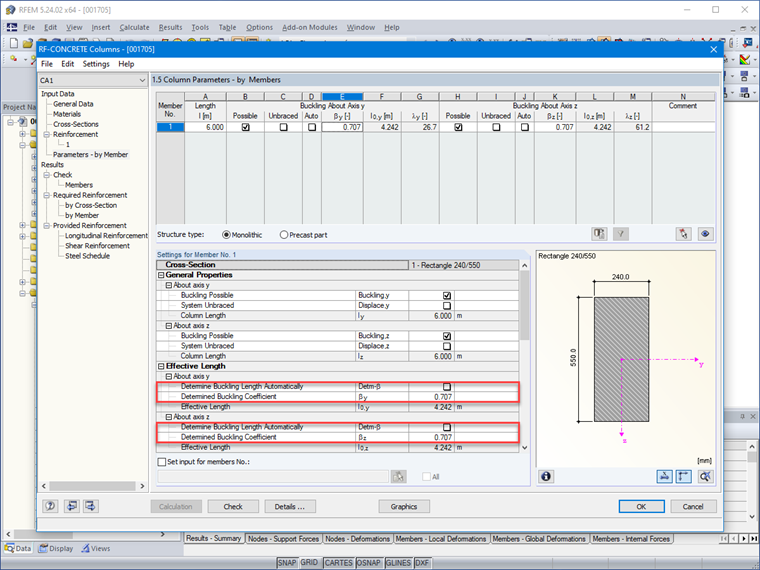
A Figura 01 mostra a possibilidade no RF-CONCRETE Columns de selecionar o coeficiente do comprimento de encurvadura β através da modelação das condições de apoio de elementos isolados com secção constante e o comprimento livre l.

1 Valores predefinidos do coeficiente de comprimento de encurvadura em torno do eixo Y

Critério de esbelteza para elementos isolados

É assumido que os efeitos de segunda ordem podem ser negligenciados se for verificado que o coeficiente de esbelteza é inferior ao critério de esbelteza.

λ < λ_{\lim}

λ_{\lim} = \frac{20 \cdot A \cdot B \cdot C}{\sqrt{n}} selon l ’ AN française

A = \frac{1}{1 + 0, 2 \cdot φ_{ef}} = 0, 7 si φ_{ef} est inconnu

B = \sqrt{1 + 2 \cdot ω} = 1, 1 si ω est inconnu

C = 1, 7 - r_{m} = 0, 7 si r_{m} est inconnu

n = \frac{N_{Ed}}{A_{C} \cdot f_{cd}}

r_{m} = \{\begin{cases} 1, si éléments non contreventés en général \\ 1, si éléments contreventés avec moments du premier ordre dus principalement à des imperfections ou à des charges transversales \\ \frac{M_{01}}{M_{02}} \leq 1, si autres cas \end{cases}

λ	Critério de esbelteza
λ_lim	Esbelteza limite
φ_ef	Coeficiente de fluência efetivo
ω	Relação de armadura mecânica
r_m	Relação de momentos
M₀₁, M₀₂	Valores algébricos dos momentos geometricamente lineares nas duas extremidades do elemento

Critério de esbelteza

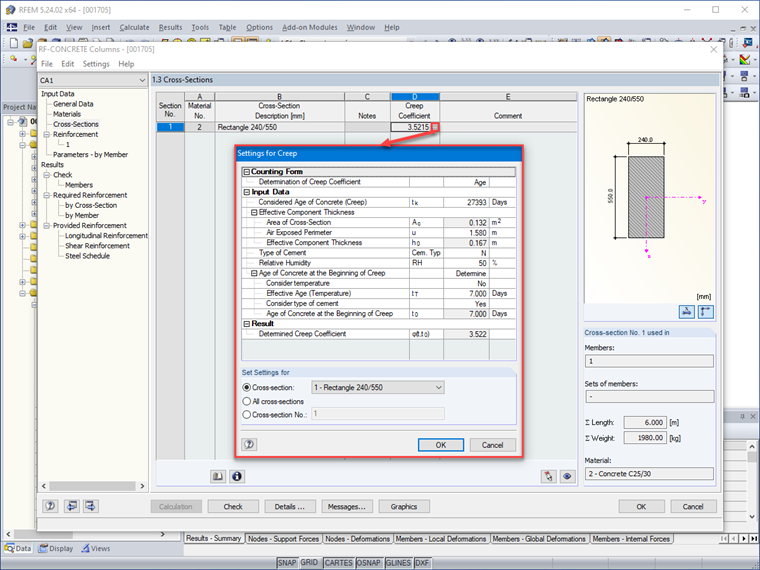
Consideração da fluência

O efeito da fluência deve ser considerado na análise de segunda ordem, considerando as condições gerais de fluência e a duração da aplicação de diferentes cargas de forma simplificada através de um coeficiente de fluência efetivo.

φ_{ef} = φ (\infty, t_{0}) \cdot \frac{M_{0 E_{qp}}}{M_{0 Ed}}

φ_ef	Coeficiente de fluência efetivo
φ(∞,t₀)	Valor final do coeficiente de fluência
M_0Eqp	Momento de utilização da primeira ordem sob combinação de ações quase-permanente
M_0Ed	Momento último de primeira ordem sob combinação de cargas de cálculo (incluindo imperfeições geométricas)

Coeficiente de fluência efetiva

2 Parâmetros de fluência nos dados de entrada

Paredes e pilares isolados de estruturas contraventadas

No caso de elementos isolados, o efeito das imperfeições pode ser considerado como excentricidade_ei.

e_{i} = θ_{i} \cdot \frac{l_{0}}{2}

θ_{i} = θ_{0} \cdot α_{h} \cdot α_{m}

θ_{0} = \frac{1}{200}

\frac{2}{3} \leq α_{h} = \frac{2}{\sqrt{l}} \leq 1

α_{m} = \sqrt{0, 5 \cdot (1 + \frac{1}{m})}

e_i	Excentricidade devido a imperfeições
θ_i	Inclinação geral da estrutura
θ₀	Valor de base recomendado pelo AN
α_h	Coeficiente de redução relativamente ao comprimento
α_m	Coeficiente de redução relativo ao número de elementos, em que m é o número de elementos verticais que contribuem para o efeito total

Excentricidade devido a imperfeições

Secções retas com armadura simétrica

Para ter em consideração os desvios nas dimensões das secções, o momento fletor deve ser calculado no ULS:

M_{E {dG}_{0}} = M_{Ed} + N_{Ed} \cdot ∆ e_{0}

∆ e_{0} = Ma x \{\begin{cases} 20 mm \\ \frac{h}{30} : excentricité minimale requise \end{cases}

M_EdG0	Momento fletor
M_Ed	Valor de cálculo do momento fletor
Δe₀	Excentricidade mínima necessária
h	Altura da secção reta no plano de flexão

Momento fletor

Cálculo de aços através de 'diagramas de interação

Os diagramas de interação momento-força normal são gráficos que permitem o dimensionamento ou a verificação rápidos de secções retas cuja forma e distribuição de armaduras são determinadas previamente. Os diagramas de interação são definidos apenas para o estado limite último. Um diagrama de interação é desenhado a partir de 2 curvas que constituem um contorno contínuo e fechado designado por curva de interação. O percurso destas curvas é baseado nas equações da resultante e do momento resultante, dependendo em particular dos seguintes parâmetros:

Diagramas de deformação de betão e aço
Diagramas de tensões de betão e aço

Assim, para a secção dada (betão, armadura, posição do aço de armadura), são definidas quantidades sem dimensão, com base nas forças internas de dimensionamento N_Ed e M_EdG0.

ν_{Ed} = \frac{N_{Ed}}{A_{c} \cdot f_{cd}}

A_{c} = b \cdot h

ν_Ed	Força axial normalizada
A_c	Área total da secção de betão puro
b	Largura da secção reta no plano de flexão
f_cd	Valor de cálculo da resistência à compressão do betão

Força axial normalizada

μ_{Ed} = \frac{M_{{EdG}_{0}}}{A_{c} \cdot h \cdot f_{cd}}

μ_Ed	Momento fletor reduzido em G₀

Momento fletor reduzido em G0

ρ = \frac{A_{s} \cdot f_{yd}}{A_{c} \cdot f_{cd}}

ρ	Percentagem mecânica da armadura
A_s	Área de armadura
f_yd	Limite de elasticidade de cálculo de aço para betão armado

Porcentagem mecânica de armadura

A última equação permite-nos determinar a secção de armadura necessária através da interpolação dos campos de curva ρ do diagrama de interacção utilizando o sistema de coordenadas ortonormal reduzido (μ, υ).

Comparação da teoria com o módulo adicional RF-CONCRETE Columns

Utilizando um exemplo simples, comparamos os resultados no RF-CONCRETE Columns com as fórmulas teóricas descritas anteriormente.

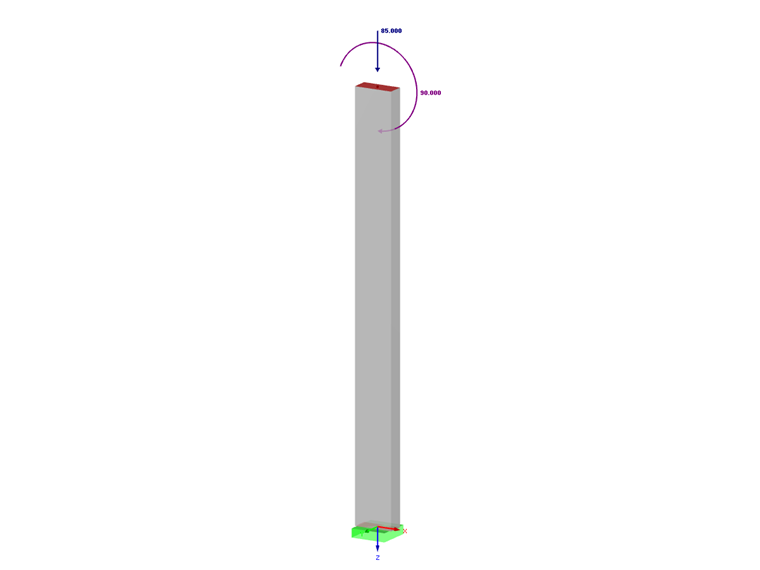
Carga aplicada ao centro de gravidade do betão puro, de um elemento de uma estrutura contraventada:
- Permanente:
  - _Ng = 85 kN
  - M_g = 90 kN.m
- Variável:
  - N_q = 75 kN
  - M_q = 80 kNm
Materiais:
- Betão C 25/30
- Aço: S 500
Relação de momentos na base do pilar:
- |M01:| / |M02| = 1/3

3 Modelo do RFEM com cargas permanentes modeladas

Características do material

f_{cd} = α_{cc} \cdot \frac{f_{ck}}{γ_{c}}

f_cd	Valor de cálculo da resistência à compressão do betão
α_cc	Fator para consideração de ações de longo prazo sobre resistência à compressão
f_ck	Resistência característica à compressão do betão
γ_c	Coeficiente de segurança parcial para betão

Valor de cálculo da resistência à compressão do betão

f_cd = 1 ⋅ 25/1,5 = 16,67 MPa

f_{y d} = \frac{f_{y k}}{γ_{s}}

f_yk	Tensão de cedência característica do aço de armadura
γ_s	Coeficiente de segurança parcial para aço de armadura

Tensão de cedência de cálculo do aço

f_yd = 500/1,15 = 434,78 MPa

estado limite último

Carregamento dos cálculos no estado limite último:
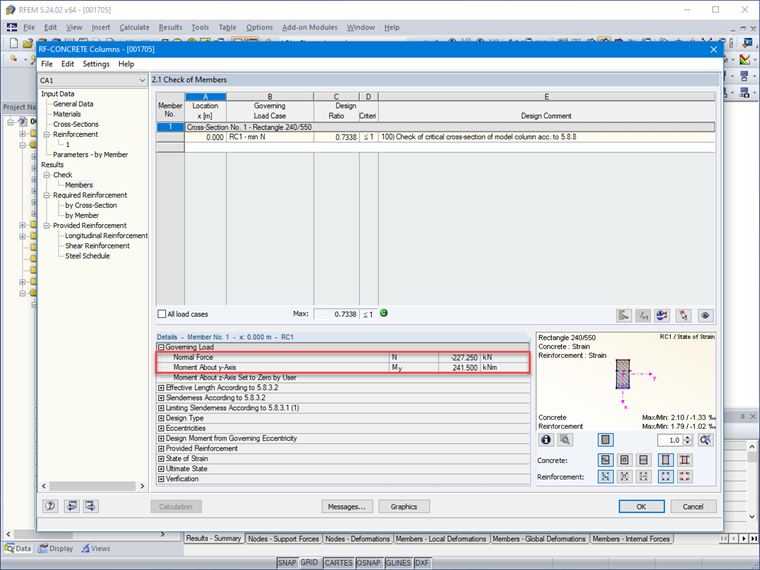
M_Ed = 1,35 ⋅ M_g + 1,5 ⋅ M_q
M_Ed = 1,35 ⋅ 90 + 1,5 ⋅ 80 = 241,50 kNm
N_Ed = 1,35 ⋅ N_g + 1,5 ⋅ N_q
N_Ed = 1,35 ⋅ 85 + 1,5 ⋅ 75 = 227,25 kN

4 Representação das cargas determinantes

Consideração de imperfeições geométricas sem efeitos de segunda ordem no ULS

Esbelteza geométrica para elementos isolados, considerando o pilar inserido num bloco de fundação e restringido por uma viga:
l₀ = √2/2 ⋅ l = √2/2 ⋅ 6,00 = 4,24 m

5 Coeficientes de encurvadura definidos pelo utilizador nos dados de entrada

Raio de giração no plano paralelo ao lado h = 55 cm
i_y = h/√12 = 0,55/√12 = 0,159 m

Raio de giração no plano paralelo ao lado h = 24 cm
i_z = b/√12 = 0,24/√12 = 0,069 m

Esbeltezas
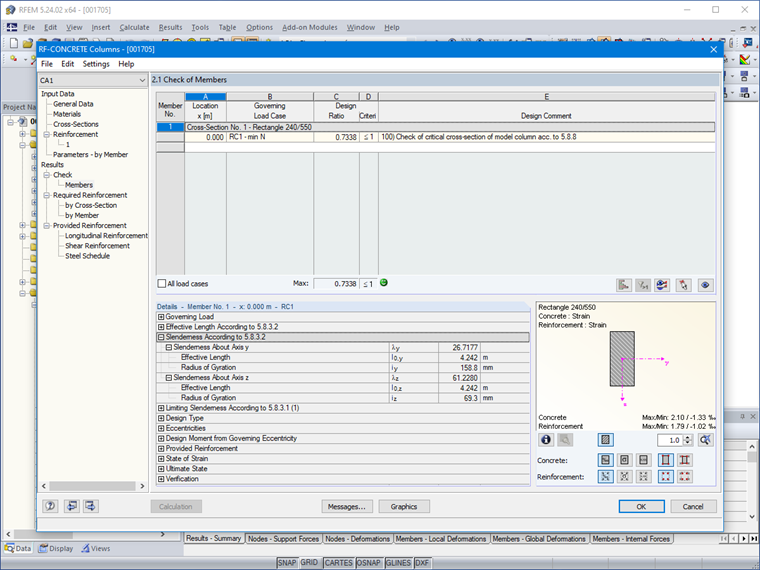
λ_y = 4,24/0,159 = 26,67 m
λ_z = 4,24/0,069 = 61,45 m

6 Apresentação de valores de esbelteza

Limitar esbelteza:
Por defeito, o programa tem em consideração os valores de acordo com os efeitos de fluência para A, as armaduras iniciais definidas no RF-CONCRETE Columns para B e a relação dos momentos na parte superior e inferior da barra analisada para C. No entanto, é possível definir esses valores por si mesmo:
A = 0,7
B = 1,1
C = 1,7 - 1/3 = 1,37
n = (227,25 ⋅^10-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
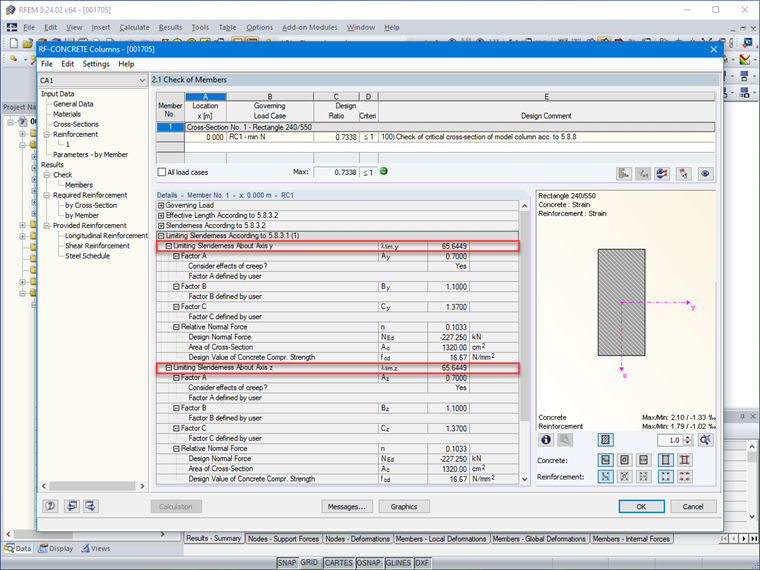
λ_lim = (20 ⋅ 0,7 ⋅ 1,1 ⋅ 1,37)/√(0,103) = 65,74
λ_y < λ_lim ⟹ cálculo de flexão combinado no plano XZ
cálculo de λ_z < λ_lim ⟹ para compressão simples no plano XY

7 Exibição dos limites da relação de esbelteza

Sendo os coeficientes de esbelteza inferiores aos valores limite, é vão verificar a parte quanto à encurvadura, e é suficiente ter um cálculo para a flexão combinada sem ter em consideração os efeitos de segunda ordem, sob as seguintes tensões de excentricidade:
e₀ = e₁ + e_i

Excentricidade devido a carregamento computacional
e₁ = M_Ed/N_Ed
e₁: Excentricidade devido a carregamento computacional
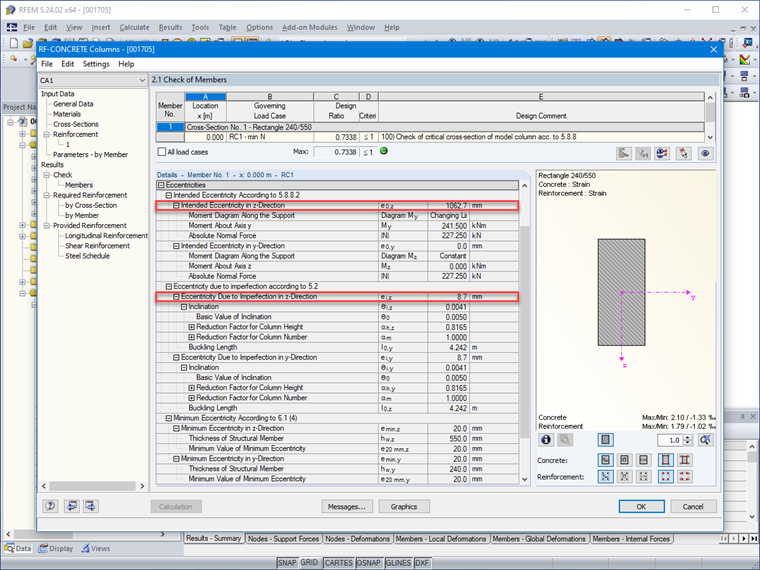
e₁ = 241,50/227,25 = 1,063 m

Carga corrigida para cálculo de flexão combinada

Pilar isolado de estrutura contraventada:
θ₀ = 1/200
α_h = 2/√6 = 0,816
α_m = √0,5 ⋅ (1 + 1/1) = 1
θ_i = 0,816 ⋅ 1/200 = 0,0041
e_i = 0,0041 ⋅ 4,24/2 = 0,0087 m

∆ e_{0} = Max \{\begin{cases} 20 mm \\ \frac{50}{30} \end{cases} = Max \{\begin{array}{l} 20 mm \\ 1, 83 mm \end{array} = 20 mm

Secção Reta com Armadura Simétrica

8 Detalhes do cálculo de excentricidade

Carga aplicada ao centro de gravidade da secção de betão puro

e₀ = e₁ + e_i ≥ Δe₀
e₀ = 1,063 + 0,0087 = 1,072 m

A excentricidade mínima foi respeitada.
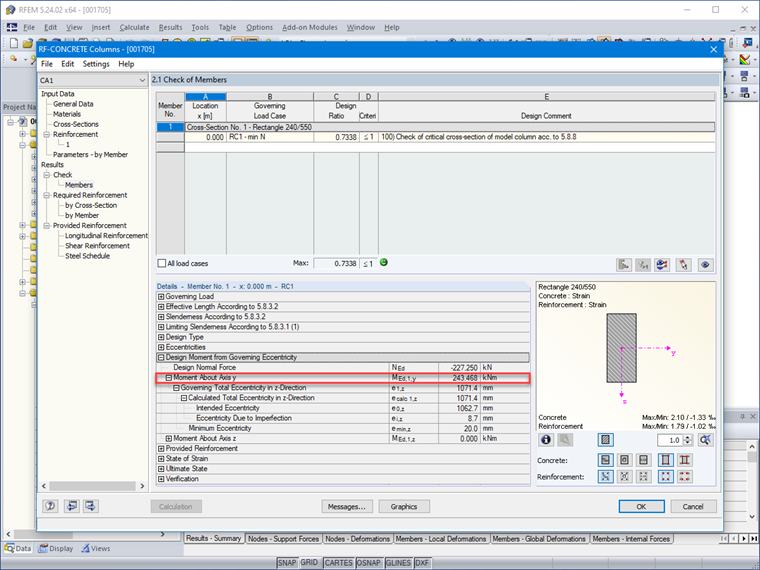
M_EdG0 = 227,25 ⋅ 1,072 = 243,61 kNm

9 Representação do momento dominante devido à excentricidade

Diagrama de interação para uma secção retangular com armadura simétrica em flexão combinada

ν_Ed = (227,25 ⋅ 10^-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
µ_Ed = (243,61 ⋅ 10^-3 )/(0,24 ⋅ 0,55² ⋅ 16,67) = 0,201

O diagrama de interação utilizado para determinar a armadura necessária de acordo com as forças reduzidas ν_Ed, μ_Ed pode ser consultado nas tabelas dos diagramas de interação (Jean^Perchat, Traité de béton armé, 3 a edição do LE Moniteur, França 2017).

Na saída gráfica, o valor encontrado é então interpolado entre as curvas de interação ρ = 0,35 e ρ = 0,40, resultando em ρ = 0,375.
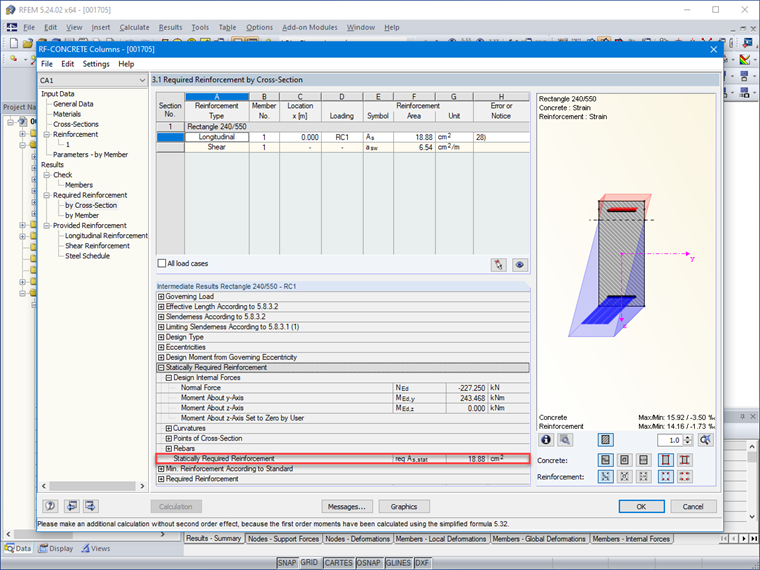
A_s = (0,375 ⋅ 0,24 ⋅ 0,55 ⋅ 16,67)/(434,78) ⋅ 10⁴ = 18,98 cm²