13486x

001705

M.Eng. Milan Gérard

2021-02-05

Obliczenia słupów betonowych poddanych zginaniu kombinowanemu z wykorzystaniem modułu RF-CONCRETE Columns

W artykule omówiono elementy, w odniesieniu do których przekrój jest poddany jednocześnie działaniu momentu zginającego, siły tnącej oraz osiowej siły ściskającej lub rozciągającej. W naszym przykładzie nie uwzględnimy jednak obciążenia siłą tnącą.

Co to jest zginanie złożone?

Zginanie złożone jest wyznaczane przez układ (M_G0, N ) przyłożony w punkcie C, zwanym środkiem ciśnienia. Odległość G₀ C jest nazywana mimośrodem siły zewnętrznej w stosunku do środka ciężkości G₀ przekroju z betonu.

Przy zginaniu kombinowanym wartość momentu zginającego zależy zatem tylko od tego punktu, w którym następuje redukcja sił; tutaj jest to G₀.

e_{0} = \frac{M_{{EdG}_{0}}}{N_{Ed}}

e₀	Mimośród względem środka ciężkości przekroju z czystego betonu
M_EdG0	Obliczeniowa wartość momentu zginającego względem środka ciężkości przekroju z czystego betonu
N_Ed	Obliczeniowa wartość działającej siły osiowej

Mimośród w stosunku do środka ciężkości przekroju czystego betonu

Pierwszą rzeczą do zrobienia w przypadku zginania złożonego jest znalezienie położenia środka ciśnienia poprzez obliczenie e₀.

Uwzględnianie imperfekcji geometrycznych i efektów drugiego rzędu w U'

Analiza elementów i konstrukcji musi uwzględniać niekorzystne wpływy imperfekcji geometrycznych w konstrukcji oraz odchyłki położenia obciążeń. Odchylenia w wymiarach przekrojów ' są zazwyczaj uwzględniane przez częściowe współczynniki bezpieczeństwa dla materiałów.

Smukłość i długość efektywna izolowanych elementów

λ = \frac{l_{0}}{i}

l_{0} = β \cdot l

λ	Współczynnik smukłości
l₀	Wyznaczona długość efektywna
i	Promień bezwładności niezarysowanego przekroju betonowego
β	Współczynnik długości wyboczeniowej
l	Długość swobodna

smukłość

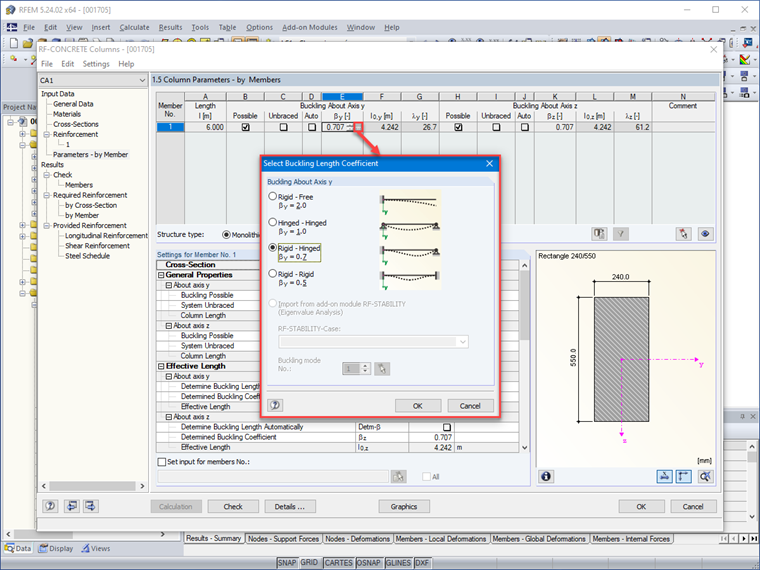
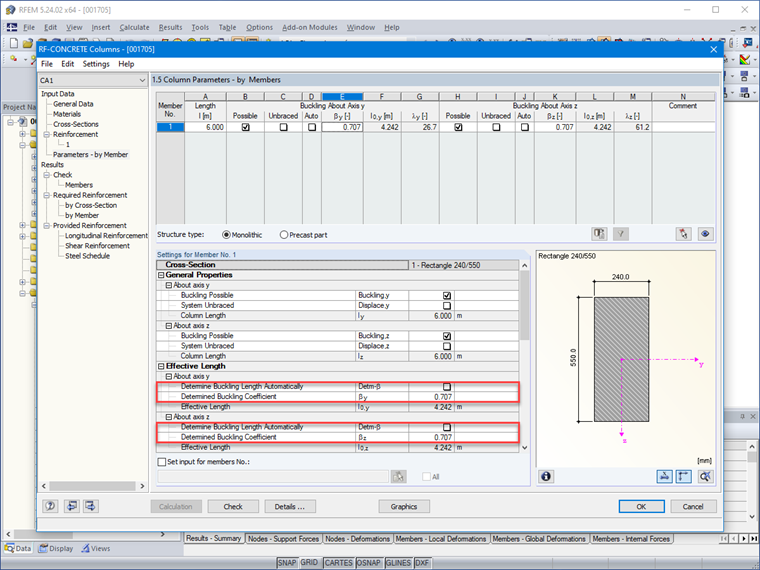
Rysunek 01 przedstawia możliwość wyboru w module RF-CONCRETE Columns współczynnika długości wyboczeniowej β poprzez zamodelowanie warunków podparcia elementów izolowanych o stałym przekroju i długości swobodnej l.

1 Wstępnie zdefiniowane wartości współczynnika długości wyboczeniowej wokół osi Y.

Kryterium smukłości dla elementów izolowanych

Zakłada się, że efekty drugiego rzędu mogą być pominięte, jeżeli zostanie zweryfikowane, że współczynnik smukłości jest mniejszy niż kryterium smukłości.

λ < λ_{\lim}

λ_{\lim} = \frac{20 \cdot A \cdot B \cdot C}{\sqrt{n}} selon l ’ AN française

A = \frac{1}{1 + 0, 2 \cdot φ_{ef}} = 0, 7 si φ_{ef} est inconnu

B = \sqrt{1 + 2 \cdot ω} = 1, 1 si ω est inconnu

C = 1, 7 - r_{m} = 0, 7 si r_{m} est inconnu

n = \frac{N_{Ed}}{A_{C} \cdot f_{cd}}

r_{m} = \{\begin{cases} 1, si éléments non contreventés en général \\ 1, si éléments contreventés avec moments du premier ordre dus principalement à des imperfections ou à des charges transversales \\ \frac{M_{01}}{M_{02}} \leq 1, si autres cas \end{cases}

λ	Kryterium smukłości
λ_lim	Smukłość graniczna
φ_ef	Efektywny współczynnik pełzania
ω	Intensywność zbrojenia
r_m	Stosunek momentów
M₀₁, M₀₂	Wartości algebraiczne momentów geometrycznie liniowych na obu końcach elementu

Kryterium smukłości

Uwzględnienie pełzania

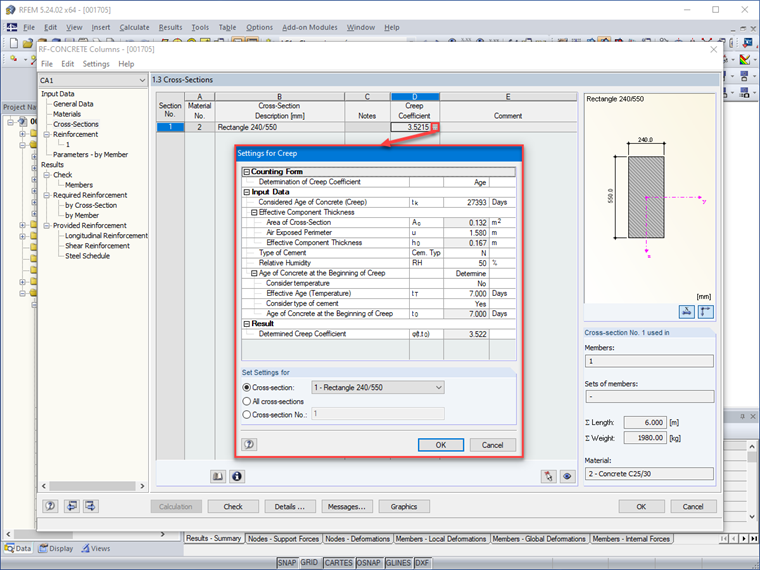
Wpływ pełzania należy uwzględnić w analizie drugiego rzędu, uwzględniając zarówno ogólne warunki pełzania, jak i czas działania różnych obciążeń w sposób uproszczony, przy użyciu efektywnego współczynnika pełzania.

φ_{ef} = φ (\infty, t_{0}) \cdot \frac{M_{0 E_{qp}}}{M_{0 Ed}}

φ_ef	Efektywny współczynnik pełzania
φ(∞,t₀)	Końcowa wartość współczynnika pełzania
M_0Eqp	Moment użytkowania pierwszego rzędu przy quasi-stałej kombinacji oddziaływań
M_0Ed	Moment brzegowy pierwszego rzędu pod wpływem kombinacji obciążeń obliczeniowych (wraz z imperfekcjami geometrycznymi)

Efektywny współczynnik pełzania

2 Parametry pełzania w danych wejściowych

Ściany i izolowane słupy konstrukcji stężonych

W przypadku elementów izolowanych efekt imperfekcji można uwzględnić jako mimośród e_i.

e_{i} = θ_{i} \cdot \frac{l_{0}}{2}

θ_{i} = θ_{0} \cdot α_{h} \cdot α_{m}

θ_{0} = \frac{1}{200}

\frac{2}{3} \leq α_{h} = \frac{2}{\sqrt{l}} \leq 1

α_{m} = \sqrt{0, 5 \cdot (1 + \frac{1}{m})}

e_i	Mimośród od imperfekcji
θ_i	Całkowite nachylenie konstrukcji
θ₀	Wartość podstawowa zalecana przez NA
α_h	Współczynnik redukcyjny odnoszący się do długości
α_m	Współczynnik redukcji odnoszący się do liczby elementów, gdzie m jest liczbą pionowych elementów wpływających na efekt całkowity

Mimośród spowodowany imperfekcjami

Proste przekroje ze zbrojeniem symetrycznym

Aby uwzględnić odchyłki w wymiarach przekrojów, moment zginający należy obliczać w SGN:

M_{E {dG}_{0}} = M_{Ed} + N_{Ed} \cdot ∆ e_{0}

∆ e_{0} = Ma x \{\begin{cases} 20 mm \\ \frac{h}{30} : excentricité minimale requise \end{cases}

M_EdG0	Moment zginający
M_Ed	Wartość obliczeniowa momentu zginającego
Δe₀	Wymagany mimośród minimalny
h	Wysokość prostego przekroju w płaszczyźnie zginania

moment zginający

Obliczanie stali przy użyciu 'wykresów interakcji

Wykresy interakcji momentu i siły normalnej to wykresy umożliwiające szybkie obliczenie lub weryfikację prostych przekrojów, których kształt i rozkład zbrojenia są wcześniej określane. Wykresy interakcji są tworzone tylko dla stanu granicznego nośności. Wykres interakcji jest rysowany za pomocą 2 krzywych tworzących ciągły i zamknięty kontur zwany krzywą interakcji. Przebieg tych krzywych oparty jest na równaniach momentu wypadkowego i wypadkowego, zależnego w szczególności od następujących parametrów:

Wykresy odkształceń betonu i stali
Wykresy naprężeń w betonie i stali

Zatem dla danego przekroju (beton, zbrojenie, położenie stali zbrojeniowej) wielkości są definiowane bezwymiarowo, na podstawie obliczeniowych sił wewnętrznych N_Ed i M_EdG0.

ν_{Ed} = \frac{N_{Ed}}{A_{c} \cdot f_{cd}}

A_{c} = b \cdot h

ν_Ed	Znormalizowana siła osiowa
A_c	Całkowite pole przekroju czystego betonu
b	Szerokość prostego przekroju w płaszczyźnie zginania
f_cd	Obliczeniowa wartość wytrzymałości betonu na ściskanie

Znormalizowana siła osiowa

μ_{Ed} = \frac{M_{{EdG}_{0}}}{A_{c} \cdot h \cdot f_{cd}}

μ_Ed	Moment zginający zredukowany w G₀

Moment zginający zredukowany w G0

ρ = \frac{A_{s} \cdot f_{yd}}{A_{c} \cdot f_{cd}}

ρ	Mechaniczny stopień zbrojenia
A_s	Pole przekroju zbrojenia
f_yd	Obliczeniowa granica plastyczności stali żelbetowej

Mechaniczna wartość procentowa zbrojenia

Ostatnie równanie pozwala nam określić niezbędny przekrój zbrojenia poprzez interpolację pól krzywych ρ wykresu interakcji przy użyciu zredukowanego ortonormalnego układu współrzędnych (μ, υ).

Porównanie teorii z modułem dodatkowym RF-CONCRETE Columns

Na prostym przykładzie porównujemy wyniki RF-CONCRETE Columns z opisanymi wcześniej wzorami teoretycznymi.

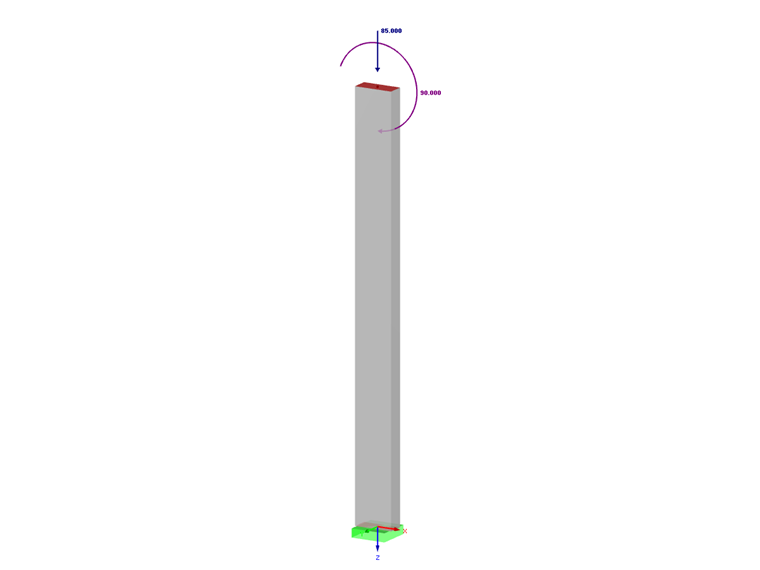
Obciążenie środka ciężkości czystego betonu elementu konstrukcji stężonej:
- Stałe:
  - N_g = 85 kN
  - _Mg = 90 kN.m
- Zmienne:
  - N_q = 75 kN
  - M_q = 80 kNm
Materiały:
- Beton C 25/30
- Stal: S 500
Stosunek momentów przy podstawie słupa:
- |M01:| / |M02| = 1/3

3 Model w RFEM z modelowanymi obciążeniami stałymi

Charakterystyki materiałowe

f_{cd} = α_{cc} \cdot \frac{f_{ck}}{γ_{c}}

f_cd	Obliczeniowa wartość wytrzymałości betonu na ściskanie
α_cc	Współczynnik uwzględniający wpływ oddziaływań długotrwałych na wytrzymałość na ściskanie
f_ck	Charakterystyczna wytrzymałość betonu na ściskanie
γ_c	Częściowy współczynnik bezpieczeństwa dla betonu

Obliczeniowa wartość wytrzymałości betonu na ściskanie

f_cd = 1 ⋅ 25/1,5 = 16,67 MPa

f_{y d} = \frac{f_{y k}}{γ_{s}}

f_yk	Charakterystyczna granica plastyczności stali zbrojeniowej
γ_s	Częściowy współczynnik bezpieczeństwa dla stali zbrojeniowej

Obliczeniowa granica plastyczności stali zbrojeniowej

f_yd = 500/1,15 = 434,78 MPa

Stan graniczny nośności

Obciążenie obliczeń w stanie granicznym nośności:
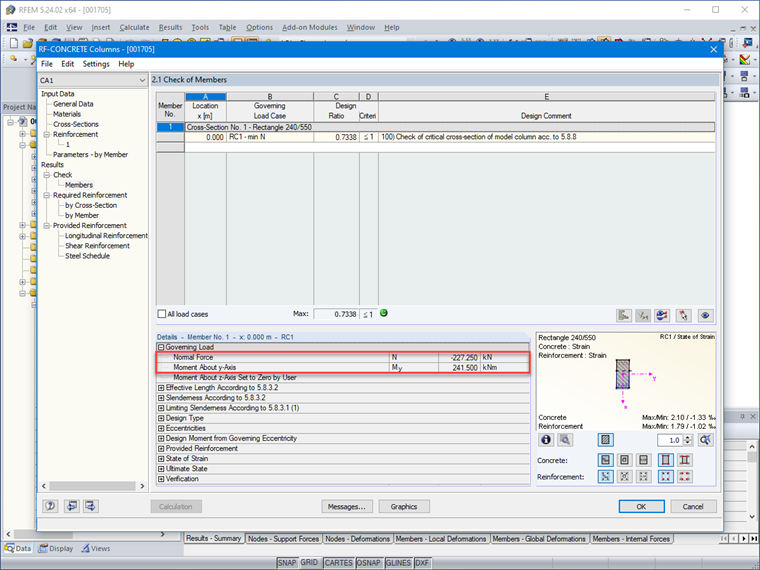
M_Ed = 1,35 ⋅ M_g + 1,5 ⋅ M_q
M_Ed = 1,35 ⋅ 90 + 1,5 ⋅ 80 = 241,50 kNm
N_Ed = 1,35 ⋅ N_g + 1,5 ⋅ N_q
N_Ed = 1,35 ⋅ 85 + 1,5 ⋅ 75 = 227,25 kN

4 Wyświetlanie obciążeń głównych

Uwzględnianie imperfekcji geometrycznych bez efektów drugiego rzędu w SGN

Smukłość geometryczna dla elementów wydzielonych, z uwzględnieniem słupa wstawionego w blok fundamentu i utwierdzonego belką:
l₀ = √2/2 ⋅ l = √2/2 ⋅ 6,00 = 4,24 m

5 Współczynniki wyboczenia zdefiniowane przez użytkownika w danych wejściowych

Promień bezwładności w płaszczyźnie równoległej do boku h = 55 cm
i_y = h/√ 12 = 0,55/√ 12 = 0,159 m

Promień bezwładności w płaszczyźnie równoległej do boku h = 24 cm
i_z = b/√ 12 = 0,24/√ 12 = 0,069 m

Smukłości
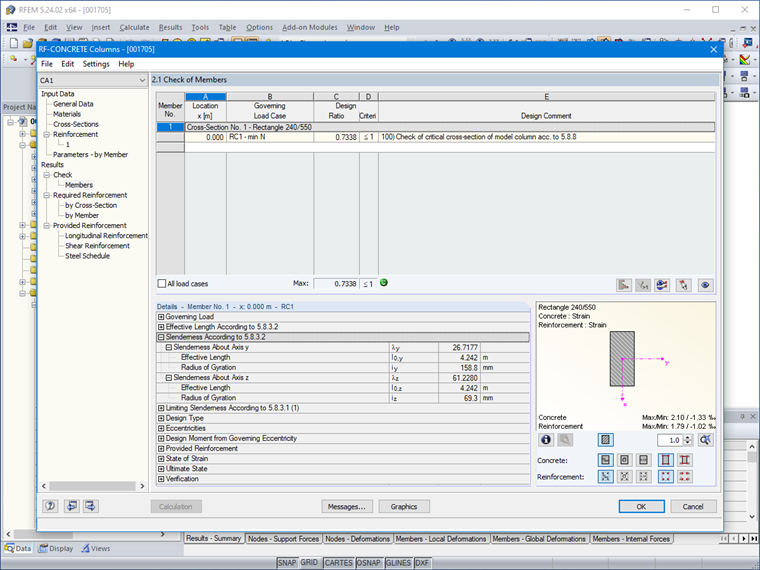
λ_y = 4,24/0,159 = 26,67 m
_λz = 4,24/0,069 = 61,45 m

6 Wyświetlanie wartości smukłości

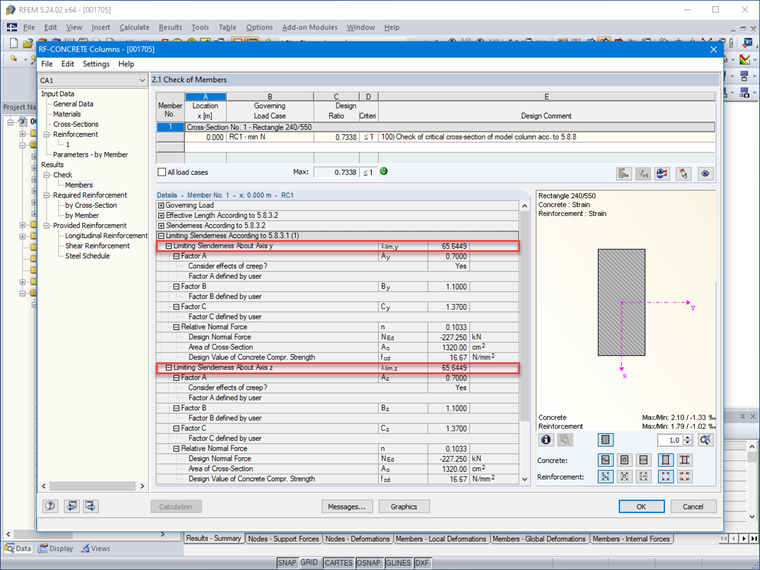
Smukłość graniczna:
Domyślnie program uwzględnia wartości wynikające z efektów pełzania dla pręta A, początkowe zbrojenie zdefiniowane w RF-CONCRETE Columns dla pręta B oraz stosunek momentów w głowicy i podstawie analizowanego pręta dla pręta C. Możliwe jest jednak samodzielne zdefiniowanie tych wartości:
A = 0,7
B = 1,1
C = 1,7 - 1/3 = 1,37
n = (227,25 ⋅^10-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
λ_lim = (20 ⋅ 0,7 ⋅ 1,1 ⋅ 1,37)/√ (0,103) = 65,74
λ_y < λ_lim obliczanie złożonego zginania w płaszczyźnie XZ
Obliczenia λ_z < λ_lim ⟹ dla zwykłego ściskania w płaszczyźnie XY

7 Wyświetlanie granic współczynnika smukłości

Ze względu na fakt, że współczynniki smukłości są mniejsze niż wartości graniczne, sprawdzenie części pod kątem wyboczenia nie ma sensu, a wystarczające są obliczenia dla zginania złożonego bez uwzględnienia efektów drugiego rzędu, przy następujących naprężeniach mimośrodowych:
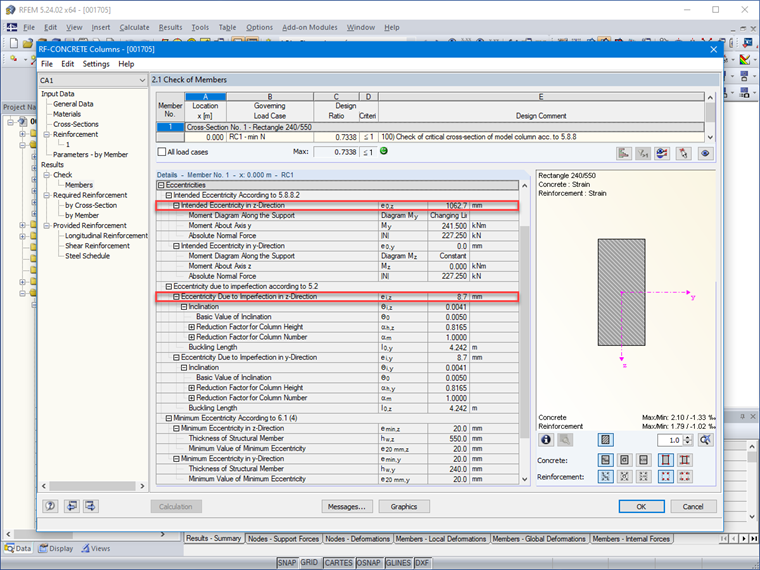
e₀ = e₁ + e_i

Mimośród od obciążenia obliczeniowego
e₁ = M_Ed/N_Ed
e₁: Mimośród od obciążenia obliczeniowego
e1 =_241,50/227,25 = 1,063 m

Obciążenie skorygowane do obliczania zginania kombinowanego

Izolowany słup z konstrukcji stężonej:
θ₀ = 1/200
α_h = 2/√6 = 0,816
α_m = √0,5 ⋅ (1 + 1/1) = 1
θ_i = 0,816 ⋅ 1/200 = 0,0041
e_i = 0,0041 ⋅ 4,24/2 = 0,0087 m

∆ e_{0} = Max \{\begin{cases} 20 mm \\ \frac{50}{30} \end{cases} = Max \{\begin{array}{l} 20 mm \\ 1, 83 mm \end{array} = 20 mm

Przekrój prosty z symetrycznym zbrojeniem

8 Szczegóły obliczeń mimośrodu

Obciążenie przyłożone do środka ciężkości przekroju z betonu

e₀ = e₁ + e_i ≥ Δe₀
e₀ = 1,063 + 0,0087 = 1,072 m

Minimalny mimośród jest zachowany.
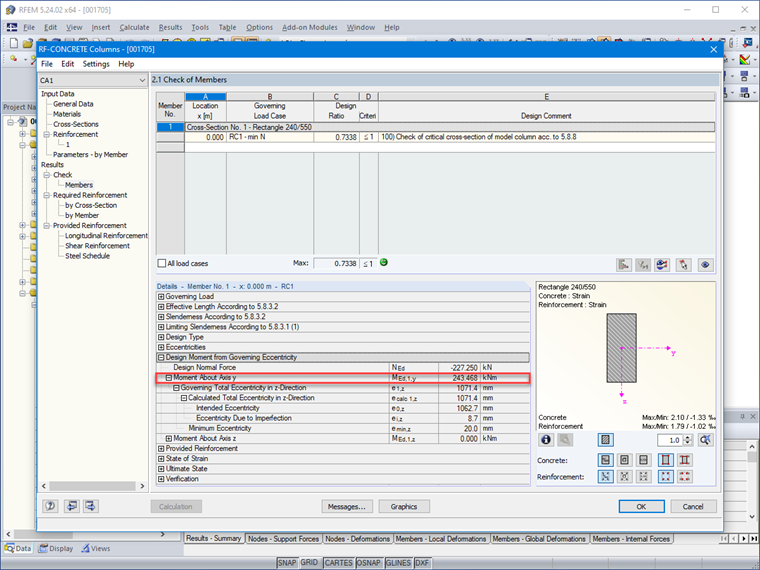
M_EdG0 = 227,25 ⋅ 1,072 = 243,61 kNm

9 Wyświetlanie decydującego momentu spowodowanego mimośrodem

Wykres interakcji dla przekroju prostokątnego z symetrycznym zbrojeniem przy zginaniu kombinowanym

ν_Ed = (227,25 ⋅^10-3 )/(0,24 ⋅ 0,55 ⋅ 16,67) = 0,103
μ_Ed = (243,61 ⋅ 10^-3 )/(0,24 ⋅ 0,55² ⋅ 16,67) = 0,201

Wykres interakcji służący do określenia wymaganego zbrojenia według sił zredukowanych ν_Ed, μ_Ed jest dostępny na wykresach wykresów interakcji (Jean Perchat, Traité de béton armé,^3. wydanie LE MONITEUR, Francja, 2017).

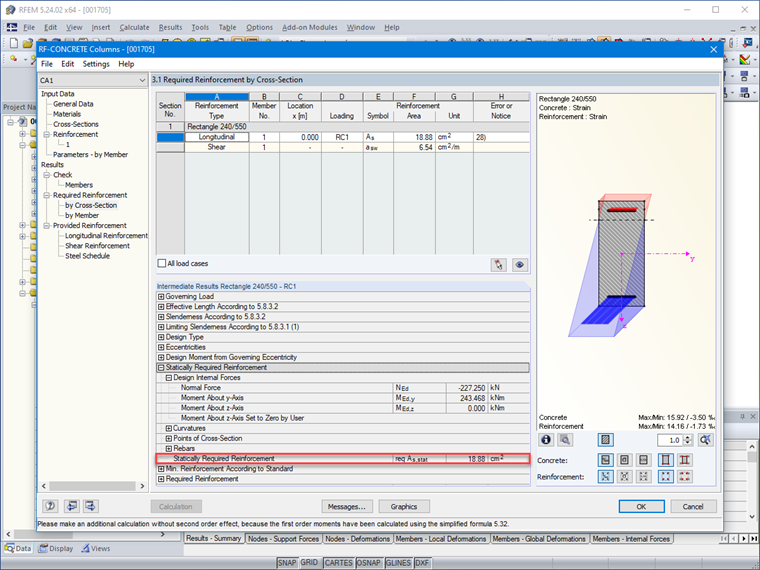
W wyniku graficznym znaleziona wartość jest następnie interpolowana między krzywymi interakcji ρ = 0,35 i ρ = 0,40, co daje ρ = 0,375.
A_s = (0,375 ⋅ 0,24 ⋅ 0,55 ⋅ 16,67)/(434,78) ⋅ 10⁴ = 18,98 cm²