Предмет:
Учет сейсмических P-Delta норм ASCE 7-22 и NBC 2020 в программе RFEM 6
Комментарий:
Легенда:
ASCE 7-22 и эффекты P-Delta
Норма ASCE 7-22 [1], разд. 12.9.1.6 далее ссылается на разд. 12.8.7 [1], в котором говорится, что в случае, если коэффициент устойчивости (θ), рассчитанный по указанному ниже уравнению, меньше или равен 0,10, эффекты P-delta не учитываются.
| Px | Общая вертикальная расчетная нагрузка на уровне и выше x по п. 12.8.6.1 (все коэффициенты нагрузок меньше или равны 1,0) |
| Vx/Δse | Жесткость этажа в уровне x, рассчитываемая как расчетный сейсмический сдвиг Vx, делённый на соответствующий упругий смещение этажа Δe |
| hsx | Высота этажа ниже уровня x |
где
P x = общая расчетная вертикальная нагрузка на уровне и выше x по п. 12.8.6.1 [1] (все коэффициенты нагрузок меньшие или равные 1,0)
Vx/Δ-se = жесткость этажа в уровне x, рассчитанная как расчетный сейсмический сдвиг Vx, делённый на соответствующий упругий смещение этажа Δ-se
h-sx = высота этажа ниже уровня x
Норма также предписывает, что θ не должно превышать меньшее из значений θ-max, найденное по ниже приведенному уравнению, поскольку конструкция является потенциально неустойчивой и требует переработку.
| Cd | Коэффициент усиления деформации в таблице 12.2-1 |
| β | Отношение требований к сдвигу к расчётной прочности на сдвиг для этажа между уровнями x и x-1 (принимается консервативно равным 1,0, но не менее 1,25/Ω0 ) |
где
Cx = коэффициент увеличения деформации в таблице 12.2-1
β = отношение требований к сдвигу к расчетной несущей способности на сдвиг для этажа между уровнями X и x-1 (принимается консервативно равным 1,0, но не менее 1,25/Ω-0)
Если значение θx меньше чем 0,10, то эффектами P-Delta можно пренебречь. Если θ-x больше, чем 0,40, тогда требуется новый расчет конструкции, поскольку при экстремальных землетрясениях она будет считаться неустойчивой. Для значений 0,10 ≤ θ-x ≤ 0,40, можно, для учета P-Delta, умножить силы и моменты, вызванные сейсмической нагрузкой на коэффициент усиления (1+θ-x). К смещениям нет необходимости применять данный коэффициент усиления.
NBC 2020 и эффекты P-Delta
В Сент. 4.1.8.3.8.c нормы NBC 2020 [2], содержится лишь краткое требование о том, что необходимо учитывать эффекты раскачивания из-за взаимодействия гравитационных нагрузок с деформированной конструкцией. Однако комментарий NBC 2015 [3]* содержит дополнительное объяснение, подобно норме ASCE 7, согласно которому коэффициент устойчивости (θ-x) в уровне x должен быть рассчитан по ниже приведенному уравнению.
| Доля постоянной и временной нагрузки на уровне x с коэффициентами | |
| Сумма расчетных сейсмических поперечных сил, действующих на уровне или выше уровня x | |
| Ro | Коэффициент модификации, связанный со сверхпрочностью |
| Δmx | Макс. неупругий междуэтажный прогиб |
| hs | Высота междуэтажа |
где
Ro = коэффициент изменения силы, связанный со сверхпрочностью
Δ-mx = максимальный неупругий междуэтажный прогиб
hs = высота междуэтажного здания
Если θ-x меньше чем 0,10, то эффекты P-Delta можно не учитывать. Если θ-x больше, чем 0,40, тогда требуется новый расчет конструкции, поскольку при экстремальных землетрясениях она будет считаться неустойчивой. Для значений 0,10 ≤ θ-x ≤ 0,40, можно, для учета P-Delta, умножить силы и моменты, вызванные сейсмической нагрузкой на коэффициент усиления (1+θ-x). К смещениям нет необходимости применять данный коэффициент усиления.
Приближенный учет эффектов P-Delta с коэффициентами усиления
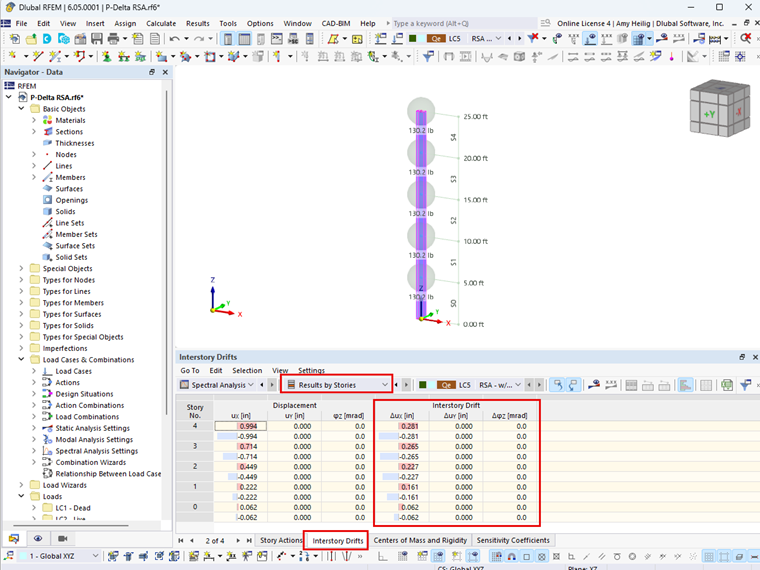
Значение коэффициента устойчивости должно быть рассчитано в обоих ортогональных горизонтальных направлениях, чтобы определить, является ли P-Delta проблемой. Требуемый смещение этажа Δ, необходимый для расчета коэффициента устойчивости в ASCE 7-22 и NBC 2020, теперь определяется автоматически в RFEM 6 с помощью аддона Building Design. Каждый уровень этажа будет включать в себя соответствующий сдвиг этажа в результатах таблицы, как показано на Рисунке 01.
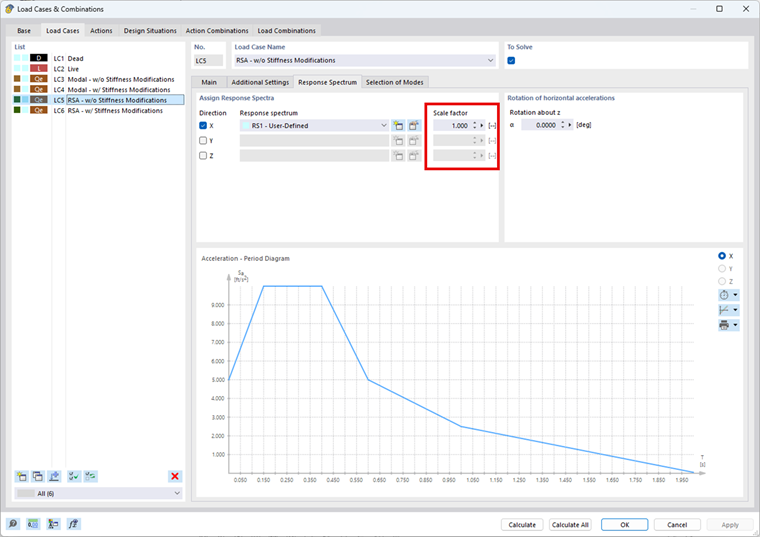
Если в одном или обоих направлениях требуется учет эффектов второго порядка в заданных диапазонах, можно легко учесть коэффициент 1,0/(1-θ) из ASCE 7-22 или (1+θ-x) из NBC 2020 в RFEM 6 и в аддоне Анализ спектра реакций. Все результирующие силы и/или прогибы будут увеличены на заданное значение.
Более точный учет эффектов P-Delta с помощью геометрической матрици жесткости
Хотя вторичные эффекты можно оценить с помощью указанных выше коэффициентов усиления, данный подход является более консервативным. Для сценариев, в которых возникают большие смещение этажей или эффекты P-Delta должны быть рассчитаны с помощью более точного подхода, влияние осевых сил можно активировать в аддоне Анализ спектра реакций.
При выполнении динамического расчета типичные нелинейные итерационные расчеты для эффектов второго порядка при учете статического расчета больше не применяются. Задача должна быть линеаризована, что выполняется путем активации геометрической матрицы жесткости во время расчета. При данном подходе предполагается, что вертикальные нагрузки не меняются из-за горизонтальных воздействий, а деформации незначительны по сравнению с габаритами конструкции [2].
Принцип геометрической матрицы жесткости - это эффект жесткости от напряжения. Растягивающие нормальные силы приведут к увеличению изгибной жесткости стержня, в то время как сжимающие нормальные силы приведут к снижению изгибной жесткости. Это можно легко передать на примере троса или тонкого стержня. Когда на стержень действует растягивающая сила, его жесткость при изгибе значительно больше, чем когда на стержень действует сжимающая сила. В случае сжатия, стержень имеет очень небольшую жесткость на изгиб, чтобы выдержать приложенную боковую нагрузку.
Геометрическая матрица жесткости Kg разрабатывается на основе условий статического равновесия.
Для упрощения, только...