知识库 001877 | RFEM 6 中需考虑的规范ASCE 7-22 和NBC 2020 地震P-Delta

主题:
RFEM 6 中需考虑的规范ASCE 7-22 和NBC 2020 地震P-Delta

注释:

论文摘要:

ASCE 7-22 和 P-Delta 效应

ASCE 7-22 规范 [1] 第 1 节12.9.1.6 进一步参见5. 12.8.7 [1]，其中当稳定系数 (θ) 由下式确定时，不需考虑 P-delta；

值:
Px = x 层每截面的总竖向设计荷载12.8.6.1 [1](所有荷载系数等于或小于 1.0)
V-x/Δ-se = the story stiffness at level x, calculated as the seismic design shear, V-x, divided by the corresponding elastic story drift, Δ-se
h-sx = the story height below level x

规范继续规定 θ 不应超过 θ-max 中的较小者，因为结构具有潜在不安全性，应重新设计。

值:
C-x = the deflection amplification factor in Table 12.2-1

β = X 和 x-1 层之间的楼层抗剪需量与抗剪承载力设计值的比值(保守取 1.0，但不小于 1.25/ω-0)

当 θx 小于 0.10 时，可以忽略 P-delta 效应。 当 θ-x 大于 0.40 时，结构应重新设计，因为它在强烈地震作用下被认为是不安全的。 当0.10 ≤ θ-x ≤ 0.40时，地震引起的力和弯矩可以乘以放大系数 (1+θ-x) 来考虑 P-delta。 该放大系数不需要用于位移。

NBC 2020 和 P-Delta 效应

在已发送中。 在 NBC 2020 [2] 的 4.1.8.3.8.c 中，只给出了一个简短的要求，即变形结构考虑重力荷载共同作用产生的侧移效应。 然而，在 NBC 2015 的注释 [3]* 中给出了与规范 ASCE 7 类似的进一步说明，其中规范 x 点的稳定性系数 (θ-x) 应使用下面的公式计算。

值:

当 θ-x 小于 0.10 时，可以忽略 P-delta 效应。 当 θ-x 大于 0.40 时，结构应重新设计，因为它在强烈地震作用下被认为是不安全的。 当0.10 ≤ θ-x ≤ 0.40时，地震引起的力和弯矩可以乘以放大系数 (1+θ-x) 来考虑 P-delta。 该放大系数不需要用于位移。

有放大系数近似考虑 P-Delta 效应

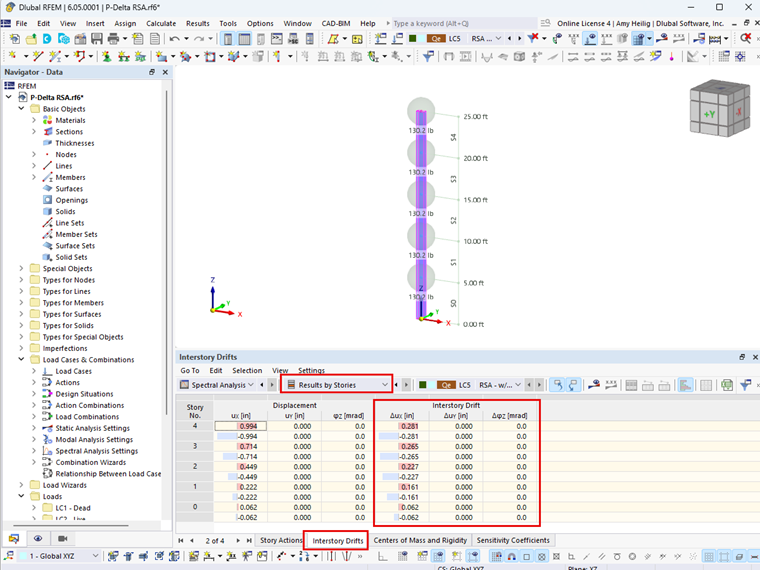
计算两个正交水平方向的稳定系数值以确定是否需要考虑 P-delta。 在 ASCE 7-22 和 NBC 2020 中计算稳定性系数所需的楼层位移 Δ，现在通过建筑设计模块在 RFEM 6 中自动给出。 Each story level will include the relevant story drift in table result output as shown in Image 01.

层间位移

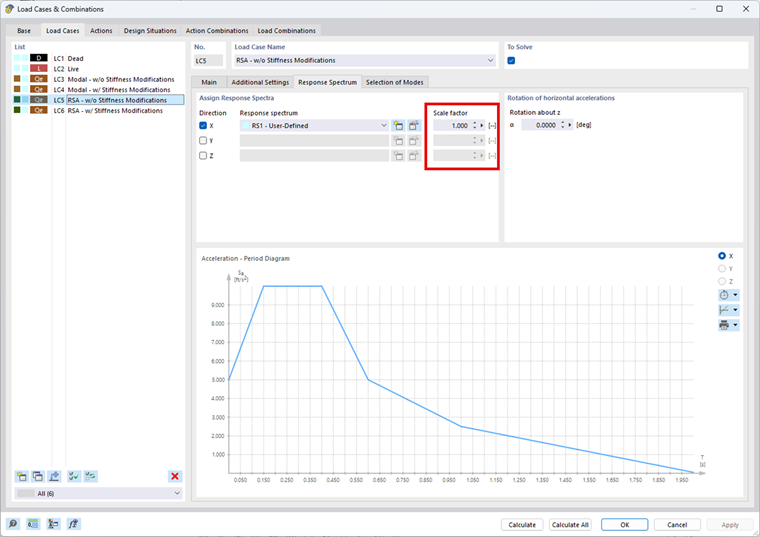
如果在一个或两个方向上需要考虑给定范围内的二阶效应，那么可以很容易地考虑 ASCE 7-22 中的系数 1.0/(1-θ) 或 NBC 2020 中的 (1+θ-x) RFEM 6 中的 响应谱分析模块 。 所有合力和/或变形都将通过放大的值放大。

缩放系数

几何刚度矩阵可以更精确地考虑 P-Delta 效应

虽然可以用上面的放大系数来估计次要效应，但这是一种更保守的方法。 如果楼层发生大位移或需要更精确地计算 P-delta 效应，则可以在反应谱分析模块中激活轴力的影响影响功能。

在进行动力分析时，在考虑静力分析时对二阶效应的典型非线性迭代计算不再适用。 该问题必须是线性化的，这可以通过在分析过程中激活几何刚度矩阵来实现。 该方法假设水平荷载在水平作用下不变，并且变形与结构的总尺寸相比较小 [2] 。

几何刚度矩阵背后的概念是应力刚化效应。 杆件受拉时会增大杆件的抗弯刚度，受压时会减小杆件的抗弯刚度。 可以简单地以绳索或细长杆件为例。 当杆件受拉时，其抗弯刚度远大于受压时的抗弯刚度。 在受压构件中，杆件的抗弯刚度非常小，无法承受侧向荷载。

几何刚度矩阵 Kg 可以由静力平衡条件下推导出来。

For simplification, only…