Soggetto:
Considerazioni sismica P-Delta di ASCE 7-22 e NBC 2020 in RFEM 6
Commento:
Descrizione:
ASCE 7-22 e P-Delta Effects
Norma ASCE 7-22 [1], sez. 12.9.1.6 si riferisce ulteriormente al cap. 12.8.7 [1], che afferma che P-delta non deve essere considerato quando il coefficiente di stabilità (θ) determinato dall'equazione seguente è uguale o inferiore a 0.10.
dove
Px = il carico di progetto verticale totale al e sopra il livello x per cap. 12.8.6.1 [1] (tutti i coefficienti di carico uguali o inferiori a 1.0)
V-x/Δ-se = the story stiffness at level x, calculated as the seismic design shear, V-x, divided by the corresponding elastic story drift, Δ-se
h-sx = the story height below level x
La norma continua a affermare che θ non dovrebbe superare il minore di θ-max, dato dall'equazione seguente, poiché la struttura è potenzialmente pericolosa e dovrebbe essere riprogettata.
dove
C-x = the deflection amplification factor in Table 12.2-1
β = rapporto tra la domanda di taglio e la capacità a taglio di progetto per il piano tra i livelli X e x-1 (preso in modo conservativo come 1.0, ma non inferiore a 1.25/Ω-0)
Quando θx è inferiore a 0,10, gli effetti P-delta possono essere ignorati. Quando θ-x è maggiore di 0,40, la struttura dovrebbe essere riprogettata poiché è considerata non sicura durante i terremoti estremi. Per 0,10 ≤ θ-x ≤ 0,40, le forze e i momenti indotti dal sisma possono essere moltiplicati per un coefficiente di amplificazione di (1+θ-x) per tenere conto di P-delta. Questo coefficiente di amplificazione non deve essere applicato agli spostamenti.
NBC 2020 e P-Delta Effects
In inviato 4.1.8.3.8.c della NBC 2020 [2], solo un breve requisito è dato che gli effetti di oscillazione dovuti all'interazione dei carichi gravitazionali con la struttura deformata dovrebbero essere considerati. Tuttavia, il Commento NBC 2015 [3]* fornisce un'ulteriore spiegazione simile alla norma ASCE 7 in cui il coefficiente di stabilità (θ-x) al livello x dovrebbe essere calcolato con l'equazione di seguito.
dove
R-o = the overstrength-related modification factor
Δ-mx = the max inelastic interstory deflection
h-s = the interstory height
Quando θ-x è inferiore a 0,10, gli effetti P-delta possono essere ignorati. Quando θ-x è maggiore di 0,40, la struttura dovrebbe essere riprogettata poiché è considerata non sicura durante i terremoti estremi. Per 0,10 ≤ θ-x ≤ 0,40, le forze e i momenti indotti dal sisma possono essere moltiplicati per un coefficiente di amplificazione di (1+θ-x) per tenere conto di P-delta. Questo coefficiente di amplificazione non deve essere applicato agli spostamenti.
Considerazione approssimativa degli effetti P-Delta con coefficienti di amplificazione
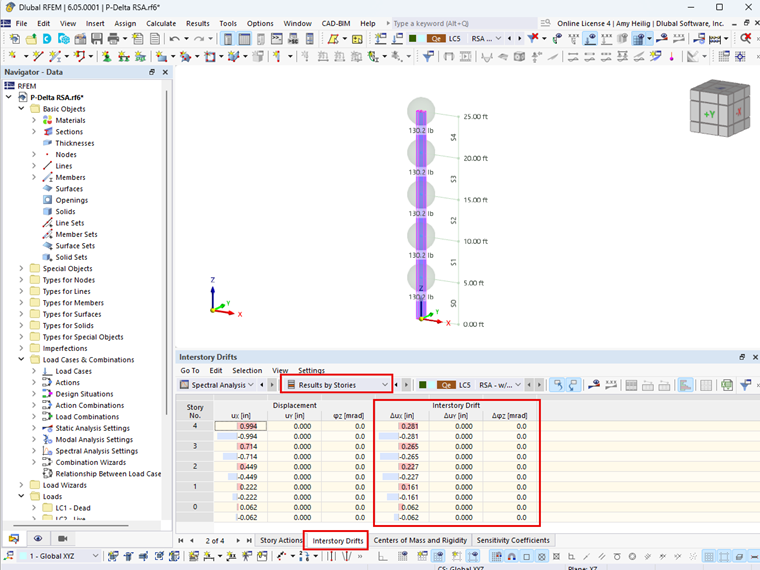
Il valore del coefficiente di stabilità dovrebbe essere calcolato in entrambe le direzioni orizzontali ortogonali per determinare se P-delta è un problema. Il drift del piano richiesto, Δ, necessario per calcolare il coefficiente di stabilità sia in ASCE 7-22 che in NBC 2020, è ora fornito automaticamente in RFEM 6 con l'add-on Verifica edifici. Each story level will include the relevant story drift in table result output as shown in Image 01.
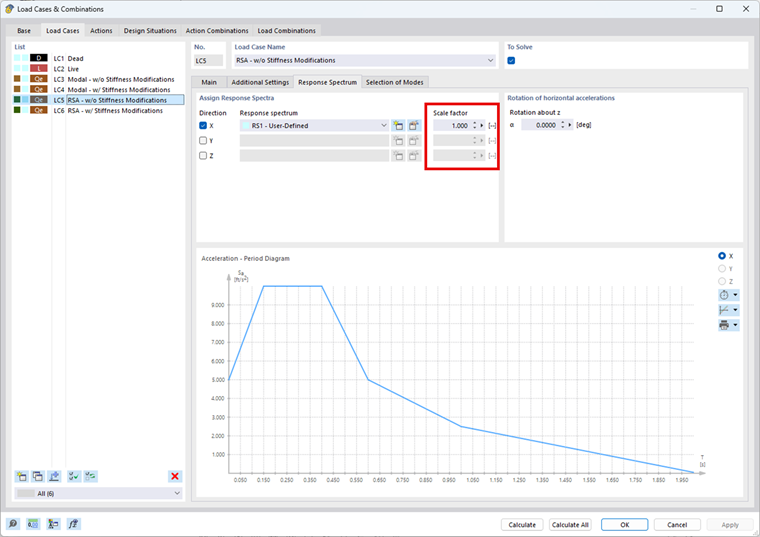
Se una o entrambe le direzioni richiedono che gli effetti del secondo ordine siano considerati all'interno degli intervalli dati, il coefficiente 1.0/(1-θ) da ASCE 7-22 o (1+θ-x) da NBC 2020 può essere facilmente considerato in RFEM 6 e nell'add-on Analisi con spettro di risposta. Tutte le forze e/o le inflessioni risultanti saranno amplificate del valore impostato.
Considerazione più precisa degli effetti P-Delta con la matrice di rigidezza geometrica
Sebbene gli effetti secondari possano essere stimati con i coefficienti di amplificazione sopra, questo è un approccio più conservativo. Per gli scenari in cui si verificano grandi derive del piano o gli effetti P-delta devono essere calcolati con un approccio più preciso, l'influenza delle forze assiali può essere attivata nell'add-on Analisi dello spettro di risposta.
Quando si esegue un'analisi dinamica, i calcoli iterativi non lineari tipici per gli effetti del secondo ordine quando si considera un'analisi statica non sono più applicabili. Il problema deve essere linearizzato, che viene eseguito attivando la matrice di rigidezza geometrica durante l'analisi. Con questo approccio, si presume che i carichi verticali non cambino a causa degli effetti orizzontali e che le deformazioni siano piccole rispetto alle dimensioni complessive della struttura [2].
Il concetto alla base della matrice di rigidezza geometrica è l'effetto di irrigidimento delle tensioni. Le forze assiali di trazione porteranno ad una maggiore rigidezza flessionale di un'asta mentre le forze assiali di compressione porteranno ad una rigidezza flessionale ridotta. Questo può essere facilmente trasportato con l'esempio di un cavo o di un'asta sottile. Quando l'asta subisce una forza di trazione, la rigidezza flessionale è significativamente maggiore rispetto a quando l'asta subisce una forza di compressione. Nel caso di compressione, l'asta ha una rigidezza flessionale minima o nulla per resistere a un carico laterale applicato.
La matrice di rigidezza geometrica Kg può essere derivata dalle condizioni di equilibrio statico.
For simplification, only…
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
