Tema:
Consideração de sismos P-Delta segundo a ASCE 7-22 e a NBC 2020 no RFEM 6
Comentário:
Descrição:
ASCE 7-22 e efeitos P-Delta
Norma ASCE 7-22 [1] , secção. 12.9.1.6 refere-se ainda à secção 12.8.7 [1] , que declara que P-delta não precisa ser considerado quando o coeficiente de estabilidade (θ) determinado pela equação abaixo é igual ou inferior a 0,10.
| Px | Total vertical design load at and above level x per Sect. 12.8.6.1 (all load factors equal to or less than 1.0) |
| Vx/Δse | Rigidez de piso no nívelx, calculada como corte sísmico de cálculo, Vx , dividido pelo correspondente deslocamento elástico do piso, Δe |
| hsx | Altura do piso abaixo do piso x |
Onde
Px = carga de cálculo vertical total no nível x e acima, por secção 12.8.6.1 [1] (todos os fatores de carga iguais ou inferiores a 1,0)
Vx/Δ-se = rigidez do piso no nível x, calculada como esforço de corte sísmico, Vx, dividido pelo correspondente deslocamento elástico do piso, Δ-se
h-sx = altura do piso abaixo do piso x
A norma continua a afirmar que θ não deve exceder o menor de θ -max , dado pela equação abaixo, porque a estrutura é potencialmente insegura e deve ser redimensionada.
| Cd | Fator de amplificação da flecha na Tabela 12.2-1 |
| β | Relação entre exigências de corte e capacidade de corte de cálculo para o piso entre os pisos x e x-1 (considerado conservadoramente como 1,0, mas não inferior a 1,25/Ω0 ) |
Onde
Cx = fator de amplificação da deformação na Tabela 12.2-1
β = relação entre a exigência de corte e a capacidade de corte de cálculo para o piso entre os pisos X e x-1 (considerado conservadoramente como 1,0, mas não inferior a 1,25/Ω-0)
Quando θx é menor que 0,10, então os efeitos P-delta podem ser ignorados. Quando θ-x é maior que 0,40, a estrutura deve ser redimensionada, pois é considerada insegura durante sismos extremos. Para 0,10 ≤ θ-x ≤ 0,40, as forças e momentos induzidos por sismos podem ser multiplicados por um fator de amplificação de (1 + θ-x ) para considerar P-delta. Este fator de amplificação não necessita de ser aplicado aos deslocamentos.
Efeitos da NBC 2020 e do P-Delta
Enviado 4.1.8.3.8.c da NBC 2020 [2], é dado apenas um pequeno requisito de que os efeitos de oscilação devido à interação das cargas de gravidade com a estrutura deformada devem ser considerados. No entanto, o comentário da NBC 2015 [3]* dá uma explicação adicional semelhante à norma ASCE 7, onde o coeficiente de estabilidade (θ-x ) no nível x deve ser calculado com a seguinte equação abaixo.
| Parte do peso próprio mais carga variável no nível x | |
| Soma das forças sísmicas laterais de cálculo atuantes ao nível x ou acima | |
| Ro | Coeficiente de alteração da força relacionado com a sobrerresistência |
| Δmx | Deflexão não-elástica entre os pisos |
| hs | Altura entre os pisos |
Onde
Ro = coeficiente de alteração da força relacionado com a sobrerresistência
Δ-mx = deflexão não-elástica entre os pisos
hs = altura entre os pisos
Quando θ-x é menor que 0,10, então os efeitos P-delta podem ser ignorados. Quando θ-x é maior que 0,40, a estrutura deve ser redimensionada, pois é considerada insegura durante sismos extremos. Para 0,10 ≤ θ-x ≤ 0,40, as forças e momentos induzidos por sismos podem ser multiplicados por um fator de amplificação de (1 + θ-x ) para considerar P-delta. Este fator de amplificação não necessita de ser aplicado aos deslocamentos.
Consideração aproximada dos efeitos P-Delta com fatores de amplificação
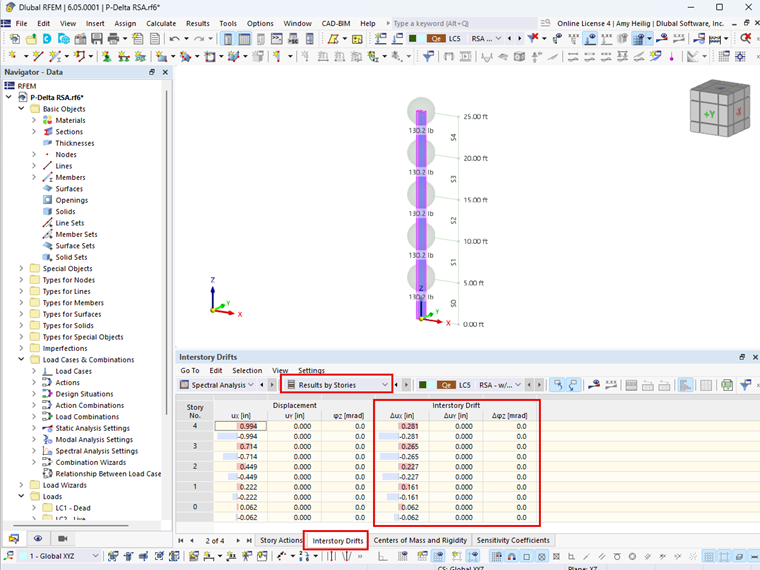
O valor do fator de estabilidade deve ser calculado nas duas direções horizontais ortogonais para determinar se P-delta é um problema. O deslocamento do piso Δ, necessário para calcular o coeficiente de estabilidade na ASCE 7-22 e na NBC 2020, é agora fornecido automaticamente no RFEM 6 com o módulo Dimensionamento do edifício. Cada nível de piso incluirá o deslocamento do piso relevante na saída de resultados da tabela como apresentado na Figura 01.
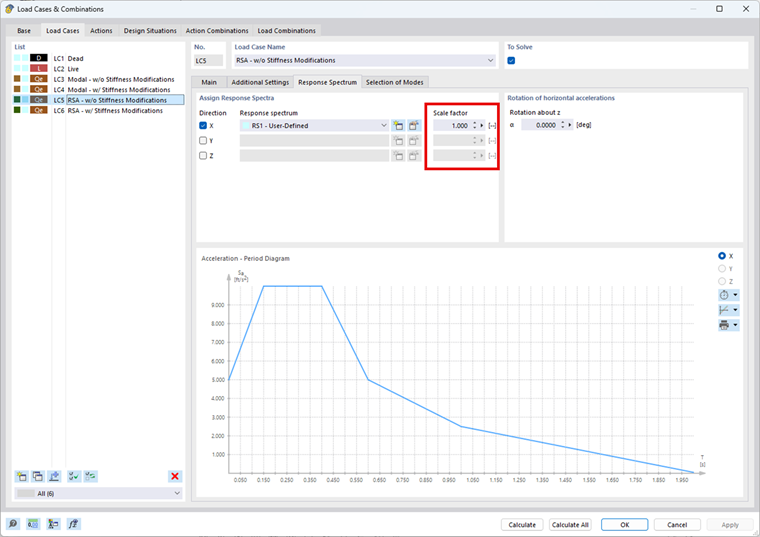
Se uma ou ambas as direções requerem que os efeitos de segunda ordem sejam considerados dentro dos intervalos dados, o fator 1,0/(1-θ) da ASCE 7-22 ou (1 + θ-x) da NBC 2020 pode ser facilmente considerado. no RFEM 6 e no módulo Análise de espectro de resposta. Todas as forças e/ou deflexões resultantes são aumentadas pelo valor definido.
Consideração mais precisa dos efeitos P-Delta com a matriz de rigidez geométrica =
Embora os efeitos secundários podem ser estimados com os fatores de amplificação acima, esta é uma abordagem mais conservadora. Para cenários onde ocorrem grandes desvios de andares ou os efeitos P-delta precisam de ser calculados com uma abordagem mais exata, a influência das forças axiais pode ser ativada no módulo Análise de espectro de resposta.
Ao realizar uma análise dinâmica, os cálculos iterativos não lineares típicos para os efeitos da análise de segunda ordem não são mais aplicáveis ao considerar uma análise estática. O problema deve ser linearizado ativando a matriz de rigidez geométrica durante o cálculo. Com esta abordagem, assume-se que as cargas verticais não se alteram devido aos efeitos horizontais e que as deformações são pequenas em comparação com as dimensões globais da estrutura [2].
O conceito por trás da matriz de rigidez geométrica é o efeito de reforço de tensões. As forças axiais de tração levarão a um aumento da resistência à flexão de uma barra, enquanto que as forças axiais de compressão levarão a uma redução da resistência à flexão. Isto pode ser facilmente transmitido com o exemplo de um cabo ou um tirante delgado. Quando a barra experimenta uma força de tração, a resistência à flexão é significativamente maior do que quando a barra está sujeita a uma força de compressão. Quando sujeita a compressão, a barra tem muito pouca ou nenhuma rigidez à flexão para suportar uma carga lateral aplicada.
A matriz de rigidez geométrica Kg pode ser derivada das condições de equilíbrio estático.
Para simplificar, apenas...