Téma:
Účinky P-Delta a seizmické posouzení podle ASCE 7-22 a NBC 2020
Komentář:
Popis:
ASCE 7-22 a P-Delta účinky
Norma ASCE 7-22 [1], čl. 12.9.1.6 dále odkazuje na čl. 12.8.7 [1], který stanoví, že P-delta není třeba zohlednit, pokud je součinitel stability (θ) stanovený pomocí níže uvedené rovnice roven nebo menší než 0,10.
| Px | Celkové návrhové svislé zatížení v úrovni x a nad ní podle čl. 12.8.6.1 (všechny součinitele zatížení se rovnají nebo jsou menší než 1,0) |
| Vx/Δse | Tuhost podlaží v úrovni x počítaná jako seizmický návrhový smyk Vx vydělený příslušným pružným posunem podlaží Δe |
| hsx | Výška podlaží pod úrovní x |
kde
Px = celkové svislé návrhové zatížení v úrovni x a nad ní podle čl. 12.8.6.1 [1] (všechny součinitele zatížení se rovnají nebo jsou menší než 1,0)
Vx/Δ-se = tuhost podlaží v úrovni x vypočítaná jako seizmický návrhový smyk Vx vydělená příslušným pružným posunem podlaží Δ-se
h-sx = výška podlaží pod podlažím x
Norma dále uvádí, že θ by nemělo překročit menší z θ-max, dané níže uvedenou rovnicí, protože konstrukce je potenciálně nebezpečná a měla by být přepracována.
| Cd | Součinitel zvětšení průhybu v tabulce 12.2-1 |
| β | Poměr smykové náročnosti k návrhové smykové únosnosti podlaží mezi podlažími x a x-1 (konzervativně 1,0, ale ne méně než 1,25/Ω0 ) |
kde
Cx = součinitel zvětšení průhybu v tabulce 12.2-1
β = poměr smykové náročnosti k návrhové smykové únosnosti podlaží mezi podlažími X a x-1 (konzervativně 1,0, ale ne méně než 1,25/Ω-0)
Pokud je θx menší než 0,10, lze účinky P-delta ignorovat. Pokud je θ-x větší než 0,40, měla by být konstrukce přepracována, protože při extrémních zemětřesení není považována za bezpečnou. Pro 0,10 ≤ θ-x ≤ 0,40 lze síly a momenty vyvolané zemětřesením vynásobit součinitelem zesílení (1+θ-x) pro zohlednění P-delta. Tento faktor zvětšení nemusí být použit u posunů.
NBC 2020 a P-delta účinky
V čl. 4.1.8.3.8.c NBC 2020 [2] je uveden pouze krátký požadavek na zohlednění účinků počátečního naklonění v důsledku interakce tíhových sil s deformovanou konstrukcí. Komentář k NBC 2015 [3]* však poskytuje další vysvětlení podobně jako norma ASCE 7, kde by se měl součinitel stability (θ-x) v úrovni x vypočítat pomocí níže uvedené rovnice.
| Část výpočtového vlastního plus užitného zatížení v úrovni x | |
| Součet návrhových příčných seizmických sil působících v úrovni x nebo nad ní | |
| Ro | Modifikační součinitel vztažený k navýšení pevnosti |
| Δmx | Maximální nepružný mezipatrový průhyb |
| hs | Mezipatrová výška |
kde
Ro = modifikační součinitel vztažený k navýšení pevnosti
Δ-mx = maximální nepružný mezipatrový průhyb
hs = výška mezi podlažími
Pokud je θ-x menší než 0,10, lze účinky P-delta ignorovat. Pokud je θ-x větší než 0,40, měla by být konstrukce přepracována, protože při extrémních zemětřesení není považována za bezpečnou. Pro 0,10 ≤ θ-x ≤ 0,40 lze síly a momenty vyvolané zemětřesením vynásobit součinitelem zesílení (1+θ-x) pro zohlednění P-delta. Tento faktor zvětšení nemusí být použit u posunů.
Přibližné zohlednění P-delta účinků se součiniteli zesílení
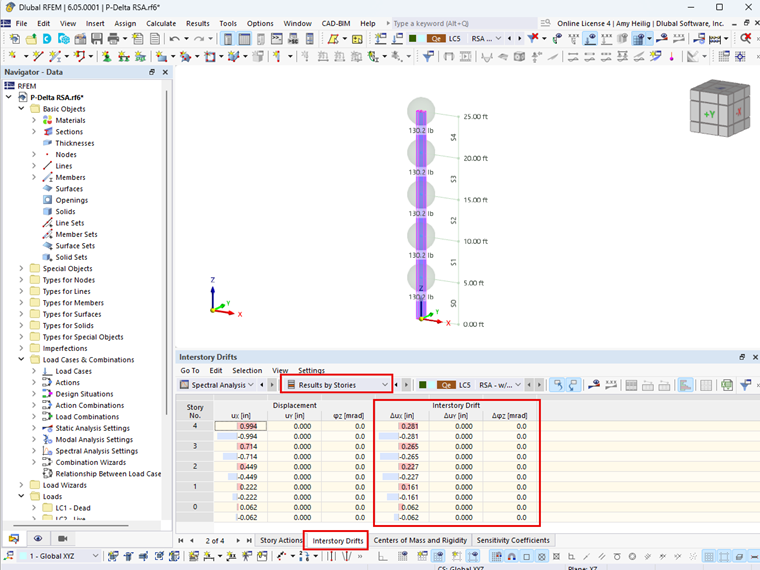
Hodnotu součinitele stability je třeba spočítat v obou ortogonálních vodorovných směrech, aby bylo možné určit, zda P-Delta představuje problém. Posun podlaží Δ nutný pro výpočet součinitele stability v normách ASCE 7-22 a NBC 2020 je nyní v programu RFEM 6 s addonem Model budovy zadáván automaticky. U každého podlaží se ve výstupu v tabulce zobrazí příslušný posun podlaží, jak je znázorněno na Obrázku 01.
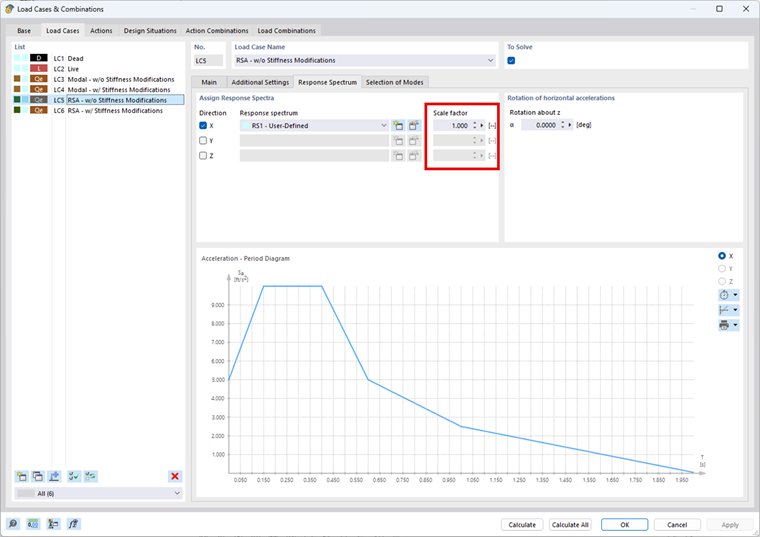
Pokud jeden nebo oba směry vyžadují zohlednění účinků druhého řádu v daných rozsazích, lze snadno zohlednit součinitel 1,0/(1-θ) z ASCE 7-22 nebo (1+θ-x) z NBC 2020 v programu RFEM 6 a addonu Analýza spektra odezvy. Všechny výsledné síly a/nebo výchylky se vynásobí nastavenou hodnotou.
Přesnější zohlednění P-delta účinků pomocí geometrické matice tuhosti
Ačkoli lze sekundární účinky odhadnout pomocí výše uvedených součinitelů zesílení, jedná se o konzervativnější přístup. Pro případy, kdy dochází k velkým posunům podlaží nebo je třeba spočítat účinky P-delta přesnějším postupem, lze v addonu Analýza spektra odezvy aktivovat vliv normálových sil.
Při dynamické analýze již nelze použít typické nelineární iterační výpočty pro účinky druhého řádu při zohlednění statické analýzy. Problém musí být linearizován, což se provádí aktivací geometrické matice tuhosti během analýzy. Při tomto přístupu se předpokládá, že svislá zatížení se v důsledku vodorovných účinků nemění a že deformace jsou ve srovnání s celkovými rozměry konstrukce malé [2].
Koncept geometrické matice tuhosti je účinek napěťového zpevnění. Tahové normálové síly vedou ke zvýšené ohybové tuhosti prutu, zatímco tlakové normálové síly vedou ke snížené ohybové tuhosti. To lze snadno přiblížit na příkladu lana nebo štíhlé tyče. Pokud na prut působí tahová síla, je ohybová tuhost výrazně větší než při působení tlakové síly. V případě tlaku má prut velmi malou nebo vůbec žádnou ohybovou tuhost, aby unesl působící boční zatížení.
Geometrickou matici tuhosti Kg lze odvodit z podmínek statické rovnováhy.
Pro zjednodušení pouze…