Przedmiot:
ASCE 7-22 i NBC 2020 Sejsmiczne uwagi P-Delta w RFEM 6
Komentarz:
Opis:
ASCE 7-22 i P-Delta Effects
ASCE 7-22 Norma [1], rozdz. 12.9.1.6 odnosi się do rozdz. 12.8.7 [1], zgodnie z którym uwzględnianie P-delta nie jest wymagane, jeżeli współczynnik stateczności (θ) określony za pomocą poniższego równania jest równy lub mniejszy niż 0,10.
| Px | Całkowite pionowe obciążenie obliczeniowe na poziomie i powyżej x na sekcję. 12.8.6.1 (wszystkie współczynniki obciążenia równe lub mniejsze niż 1.0) |
| Vx/Δse | Sztywność kondygnacji na poziomie x, obliczana jako iloraz sejsmicznego ścinania Vx i odpowiedniego znoszenia sprężystego kondygnacji, Δe |
| hsx | Wysokość kondygnacji poniżej poziomu x |
Gdzie
Px = całkowite pionowe obciążenie obliczeniowe na i powyżej poziomu x na sekcję. 12.8.6.1 [1] (wszystkie współczynniki obciążenia równe lub mniejsze niż 1.0)
Vx/Δ-se = sztywność kondygnacji na poziomie x, obliczona jako sejsmiczne ścinanie obliczeniowe Vx, podzielone przez sprężysty ślizg kondygnacji Δ-se
h-sx = wysokość kondygnacji poniżej poziomu x
Norma nadal stanowi, że θ nie powinno przekraczać mniejszej z wartości θ-max, podanej za pomocą poniższego równania, ponieważ konstrukcja jest potencjalnie niebezpieczna i powinna zostać przeprojektowana.
| Cd | Współczynnik wzmocnienia ugięcia w Tablicy 12.2-1 |
| β | Stosunek zapotrzebowania na ścinanie do obliczeniowej nośności na ścinanie dla kondygnacji między poziomami x i x-1 (przyjęty konserwatywnie jako 1,0, ale nie mniej niż 1,25/Ω0 ) |
Gdzie
Cx = współczynnik wzmocnienia ugięcia w tabeli 12.2-1
β = stosunek zapotrzebowania na ścinanie do obliczeniowej nośności na ścinanie dla kondygnacji między poziomami X i x-1 (przyjęty konserwatywnie jako 1,0, ale nie mniej niż 1,25/Ω-0)
Jeżeli θx jest mniejsze niż 0,10, efekty P-delta można zignorować. Jeżeli θ-x jest większe niż 0,40, konstrukcję należy przeprojektować, ponieważ jest uznawana za niebezpieczną podczas ekstremalnych trzęsień ziemi. Dla 0,10 ≤ θ-x ≤ 0,40, siły i momenty wywołane trzęsieniem ziemi można pomnożyć przez współczynnik (1+θ-x), aby uwzględnić P-delta. Współczynnik ten nie musi być stosowany do przemieszczeń.
NBC 2020 i efekty P-Delta
W Wysłane. 4.1.8.3.8.c NBC 2020 [2], jedynie krótki wymóg, aby uwzględnić efekty przechyłowe wynikające z interakcji obciążeń grawitacyjnych z odkształconą konstrukcją. Komentarz do NBC 2015 [3]* zawiera jednak dalsze wyjaśnienia, podobnie jak w normie ASCE 7, w której współczynnik stateczności (θ-x) na poziomie x należy obliczać przy użyciu poniższego równania.
| Część obliczeniowego obciążenia stałego plus zmiennego na poziomie x | |
| Suma obliczeniowych bocznych sił sejsmicznych działających na poziomie x . lub powyżej | |
| Ro | Współczynnik modyfikacji związany z rezerwą nośności |
| Δmx | Maksymalne niesprężyste ugięcie międzypoziomowe |
| hs | Wysokość międzykondygnacyjna |
Gdzie
Ro = współczynnik modyfikacji związany z rezerwą nośności
Δ-mx = maksymalne niesprężyste ugięcie międzykondygnacyjne
hs = wysokość międzykondygnacyjna
Jeżeli θ-x jest mniejsze niż 0,10, efekty P-delta można zignorować. Jeżeli θ-x jest większe niż 0,40, konstrukcję należy przeprojektować, ponieważ jest uznawana za niebezpieczną podczas ekstremalnych trzęsień ziemi. Dla 0,10 ≤ θ-x ≤ 0,40, siły i momenty wywołane trzęsieniem ziemi można pomnożyć przez współczynnik (1+θ-x), aby uwzględnić P-delta. Współczynnik ten nie musi być stosowany do przemieszczeń.
Przybliżone uwzględnienie efektów P-Delta ze współczynnikami wzmocnienia
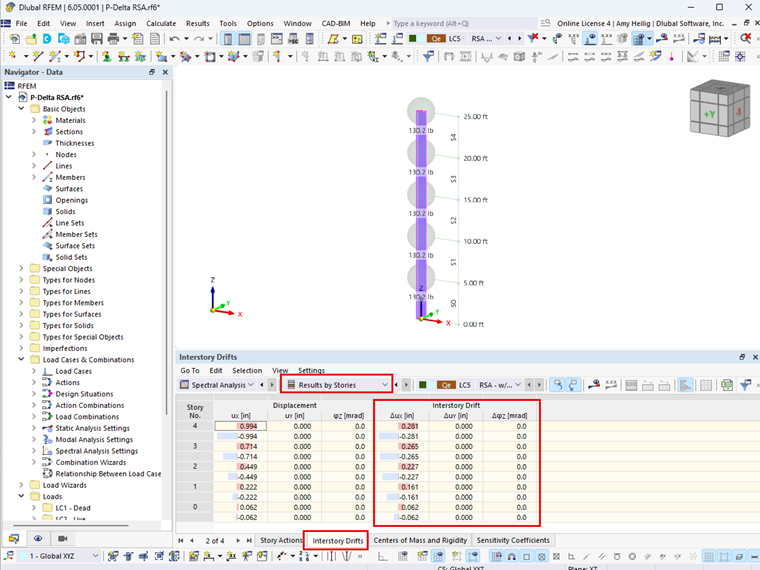
Wartość współczynnika stateczności należy obliczyć w obu ortogonalnych kierunkach poziomych, aby określić, czy parametr P-delta stanowi problem. Wymagany strop kondygnacji, Δ, niezbędny do obliczenia współczynnika stateczności zarówno w ASCE 7-22, jak i NBC 2020, jest teraz podawana automatycznie w programie RFEM 6 z rozszerzeniem Projektowanie budowlane. Dla każdego poziomu kondygnacji w tabeli wyników zostanie uwzględniony odpowiedni ślizg kondygnacji, jak pokazano na rysunku 01.
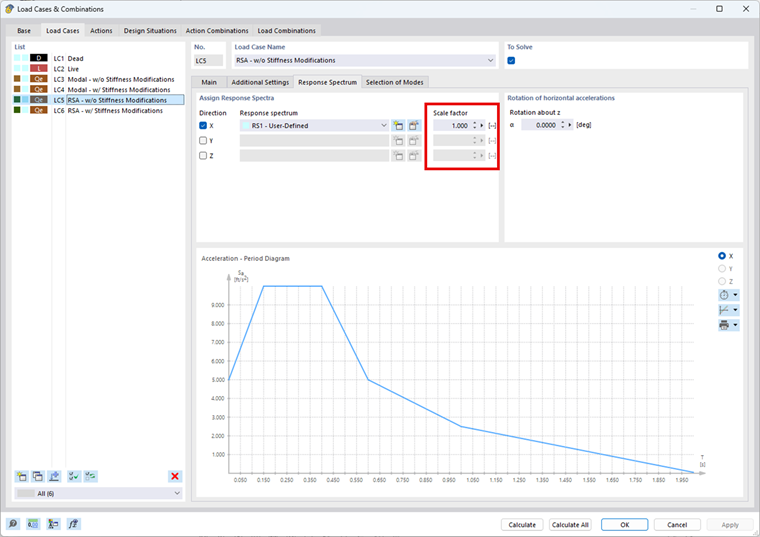
Jeżeli jeden lub oba kierunki wymagają uwzględnienia efektów drugiego rzędu w podanych zakresach, można łatwo uwzględnić współczynnik 1,0/(1-θ) z ASCE 7-22 lub (1+θ-x) z NBC 2020 w programie RFEM 6 i rozszerzeniu Analiza spektrum odpowiedzi. Wszystkie wypadkowe siły i/lub ugięcia zostaną zwiększone o zadaną wartość.
Dokładniejsze uwzględnienie efektów P-Delta przy użyciu geometrycznej macierzy sztywności
Chociaż efekty wtórne można oszacować za pomocą powyższych współczynników, jest to bardziej konserwatywne podejście. W scenariuszach, w których występują duże kondygnacje, lub konieczne jest obliczenie efektów P-delta z dokładniejszą metodą, wpływ sił osiowych można aktywować w rozszerzeniu Analiza spektrum odpowiedzi.
Podczas przeprowadzania analizy dynamicznej typowe nieliniowe obliczenia iteracyjne dla efektów drugiego rzędu w przypadku analizy statycznej nie są już stosowane. Problem musi zostać zlinearyzowany, co jest realizowane poprzez aktywację macierzy sztywności geometrycznej podczas analizy. Dzięki temu podejściu zakłada się, że obciążenia pionowe nie zmieniają się pod wpływem efektów poziomych, a odkształcenia są niewielkie w porównaniu z całkowitymi wymiarami konstrukcji [2].
Ideą macierzy sztywności geometrycznej jest efekt usztywnienia naprężeń. Rozciągające siły osiowe prowadzą do zwiększenia sztywności pręta na zginanie, a osiowe siły ściskające do zmniejszenia sztywności na zginanie. Można to łatwo przedstawić na przykładzie kabla lub smukłego pręta. W przypadku działania siły rozciągającej sztywność na zginanie jest znacznie większa niż w przypadku działania siły ściskającej. W przypadku ściskania, pręt ma bardzo małą sztywność na zginanie, aby wytrzymać przyłożone obciążenie boczne.
Geometryczną macierz sztywności Kg można wyprowadzić z warunków równowagi statycznej.
Dla uproszczenia, tylko...