Subject:
ASCE 7-22 and NBC 2020 Seismic P-Delta Considerations in RFEM 6
Comment:
Description:
ASCE 7-22 and P-Delta Effects
ASCE 7-22 Standard [1], Sect. 12.9.1.6 further refers to Sect. 12.8.7 [1], which states that P-delta does not need to be considered when the stability coefficient (θ) determined by the equation below is equal to or less than 0.10.
where
P-x = the total vertical design load at and above level x per Sect. 12.8.6.1 [1] (all load factors equal to or less than 1.0)
V-x/Δ-se = the story stiffness at level x, calculated as the seismic design shear, V-x, divided by the corresponding elastic story drift, Δ-se
h-sx = the story height below level x
The standard continues to state that θ should not exceed the lesser of θ-max, given by the equation below, as the structure is potentially unsafe and should be redesigned.
where
C-x = the deflection amplification factor in Table 12.2-1
β = ratio of shear demand to design shear capacity for the story between levels X and x-1 (taken conservatively as 1.0, but not less than 1.25/Ω-0)
When θx is less than 0.10, then P-delta effects can be ignored. When θ-x is greater than 0.40, the structure should be redesigned as it’s considered unsafe during extreme earthquakes. For 0.10 ≤ θ-x ≤ 0.40, the seismic-induced forces and moments can be multiplied by an amplification factor of (1+θ-x) to account for P-delta. This amplification factor does not need to be applied to displacements.
NBC 2020 and P-Delta Effects
In Sent. 4.1.8.3.8.c of the NBC 2020 [2], only a short requirement is given that sway effects due to the interaction of gravity loads with the deformed structure should be considered. However, the NBC 2015 Commentary [3]* gives further explanation similar to the ASCE 7 standard where the stability factor (θ-x) at level x should be calculated with the given equation below.
where
R-o = the overstrength-related modification factor
Δ-mx = the max inelastic interstory deflection
h-s = the interstory height
When θ-x is less than 0.10, then P-delta effects can be ignored. When θ-x is greater than 0.40, the structure should be redesigned as it’s considered unsafe during extreme earthquakes. For 0.10 ≤ θ-x ≤ 0.40, the seismic-induced forces and moments can be multiplied by an amplification factor of (1+θ-x) to account for P-delta. This amplification factor does not need to be applied to displacements.
Approximate Consideration of P-Delta Effects with Amplification Factors
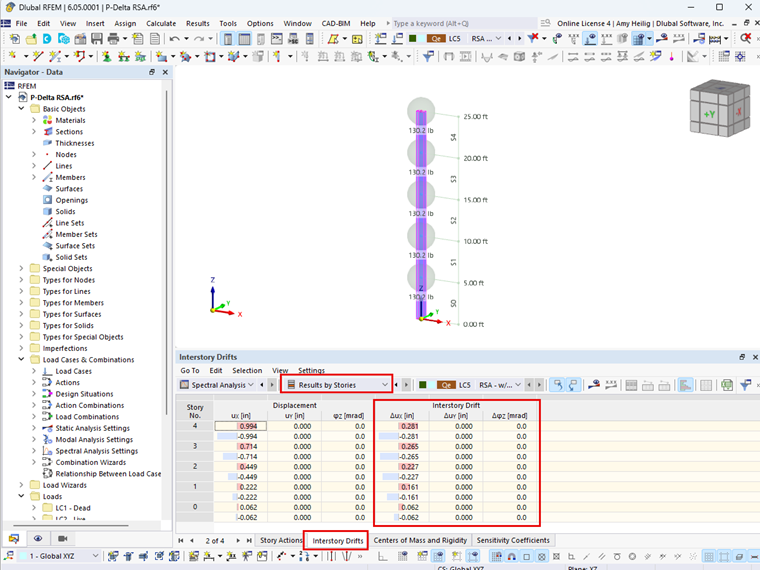
The stability factor value should be calculated in both orthogonal horizontal directions to determine if P-delta is a concern. The required story drift, Δ, necessary to calculate the stability coefficient in both the ASCE 7-22 and NBC 2020, is now given automatically in RFEM 6 with the Building Design Add-on. Each story level will include the relevant story drift in table result output as shown in Image 01.
If one or both directions require second-order effects to be considered within the given ranges, the factor 1.0/(1-θ) from the ASCE 7-22 or (1+θ-x) from the NBC 2020 can easily be accounted for in RFEM 6 and the Response Spectrum Analysis Add-on. All resulting forces and/or deflections will be amplified by the set value.
More Exact Consideration of P-Delta Effects with the Geometric Stiffness Matrix
Although secondary effects can be estimated with the amplification factors above, this is a more conservative approach. For scenarios where large story drifts occur or P-delta effects need to be calculated with a more exact approach, the influence of axial forces can be activated in the Response Spectrum Analysis Add-on.
When running a dynamic analysis, the typical nonlinear iterative calculations for second-order effects when considering a static analysis are no longer applicable. The problem must be linearized, which is carried out by activating the geometric stiffness matrix during the analysis. With this approach, it is assumed that vertical loads do not change due to horizontal effects and that deformations are small when compared to the overall dimensions of the structure [2].
The concept behind the geometric stiffness matrix is the stress stiffening effect. Tensile axial forces will lead to an increased bending stiffness of a member while compressive axial forces will lead to a reduced bending stiffness. This can be easily conveyed with the example of a cable or slender rod. When the member experiences a tension force, the bending stiffness is significantly greater than when the member is undergoing a compression force. In the case of compression, the member has very little if any bending stiffness to withstand an applied lateral load.
The geometric stiffness matrix K-g can be derived from the static equilibrium conditions.
For simplification, only…
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
