1934x

001487

Dipl.-Ing. (FH) Lukas Sühnel

2017-10-18

Перераспределение сдвигающих напряжений нулевых элементов

Программа SHAPE-THIN позволяет рассчитать характеристики и напряжения любых сечений. Если полка или стенка ослаблены отверстиями для болтов, это можно смоделировать с помощью нулевых элементов. После этого напряжения рассчитываются повторно с уменьшенными значениями сечения. Ein besonderes Augenmerk ist hierfür auf die Schubspannungen zu legen. Diese werden standardmäßig im Bereich der Nullelemente zu Null gesetzt. При пересчете сдвигающих напряжений с уменьшенными значениями сечений без дальнейшей корректировки, окажется, что интеграл сдвигающих напряжений больше не равен прилагаемой поперечной силе. Поэтому в следующем примере подробно показано, как рассчитать сдвигающее напряжение.

Пример расчета

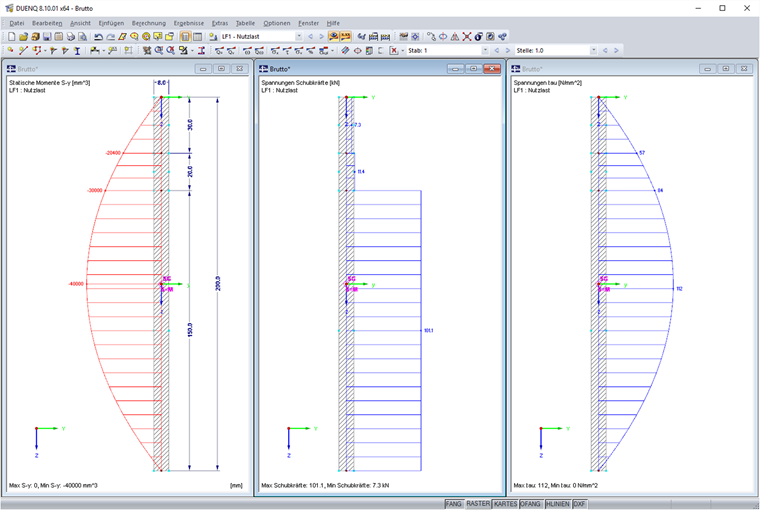
Дан элемент длиной l 200 мм и толщиной t 8 мм. Сдвигающее усилие задано равным 120 кН. В результате мы получим следующие распределения статического момента, сдвигающей силы и сдвигающего напряжения. Полученный момент инерции площади равен I_y = 533 см⁴.

Ergebnisverläufe des Brutto-Querschnitts

В данном случае сдвигающая сила - это сдвигающее напряжение, умноженное на длину и толщину соответствующего элемента. Интеграл выглядит следующим образом:

V = t \cdot \int \frac{Q \cdot (t \cdot z \cdot (\frac{l}{2} - \frac{z}{2}))}{I_{y} \cdot t} dz

Формула 1

где
z - значение координаты z.

Сложив значения трех сил, возникающие в результате выбранного разделения элемента, мы получим сдвигающую силу, равную 120 кН.

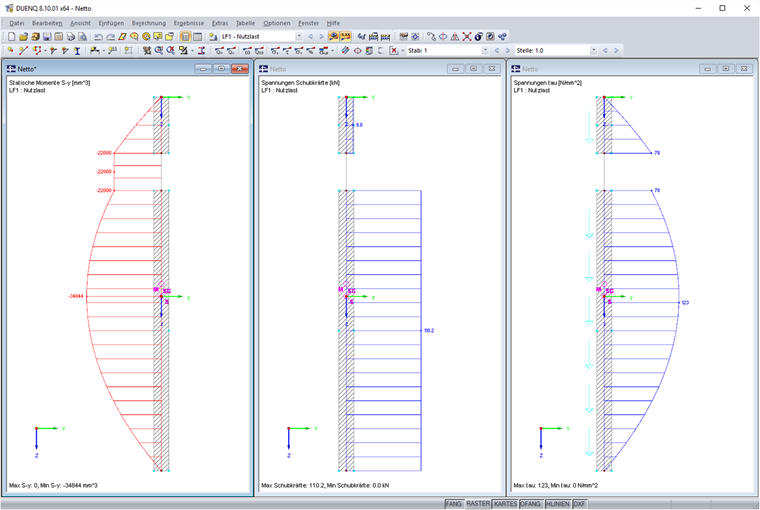
Затем средний элемент длиной 20 мм преобразуем в нулевой элемент. Он будет соответствовать вышеупомянутому отверстию. Момент инерции площади равен I_y = 469 см⁴. Сдвигающие напряжения нулевого элемента теперь должны быть распределены по другим элементам. Для этого рассчитывается поправочный коэффициент k, который представляет отношение поперечной силы к действующим составляющим сдвигающей силы.

k = \frac{Querkraft}{Summe der noch wirksamen Schubkraftanteile am Bruttoquerschnitt} = \frac{120}{101, 1 7, 3} = 1, 11

Формула 2

Затем поперечная сила умножается на этот коэффициент:
Q = 120 ∙ 1,11 = 133,2 кН

На основе данной скорректированной поперечной силы затем рассчитываются сдвигающие напряжения в ослабленном сечении. В результате мы получим следующие диаграммы статического момента, сдвигающей силы и сдвигающего напряжения.

Ergebnisverläufe des geschwächten Querschnitts

При сложении сдвигающих сил мы снова получим заданную поперечную силу 120 кН. Компоненты нулевого элемента были полностью перераспределены.

Ориентир

[1]	Руководство SHAPE-THIN. Тифенбах: Dlubal Software, Februar 2017.

Автор

Г-н Зюнель отвечает за контроль качества программы RSTAB; но он также занимается разработкой продуктов и оказывает техническую поддержку нашим клиентам.

Ссылки

Скачивания

SHAPE-THIN Model File 1

368 KB

SHAPE-THIN Model File 2

356 KB

;