Przykładowe obliczenia
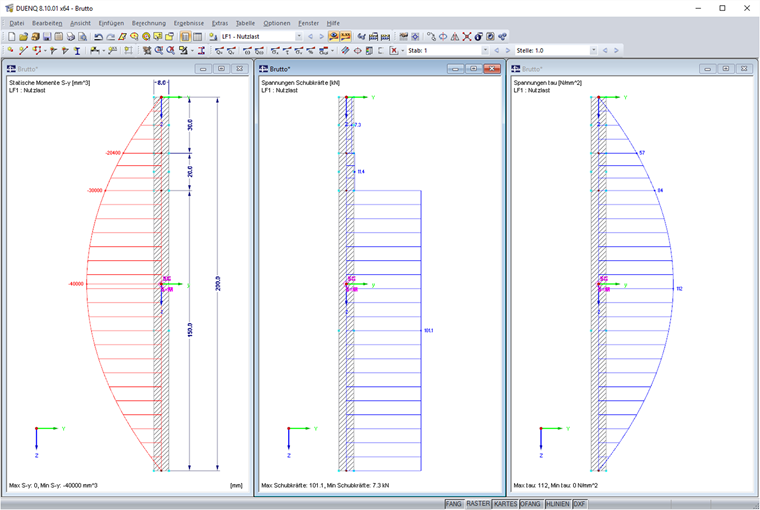
Gegeben sei ein Element der Länge l = 200 mm und der Dicke t = 8 mm. Die Querkraft wird mit 120 kN angesetzt. Daraus resultieren folgende Verläufe für statisches Moment, Schubkraft und Schubspannung. Das Flächenträgheitsmoment ergibt sich zu Iy = 533 cm4.
Die Schubkraft ist dabei die Schubspannung multipliziert mit der Länge und der Dicke des jeweiligen Elementes. Das Integral hierfür sieht wie folgt aus:
z ist hierbei der Wert der z-Koordinate.
Addiert man die drei Schubkräfte, die sich aufgrund der gewählten Elementteilung ergeben, erhält man die Querkraft von 120 kN.
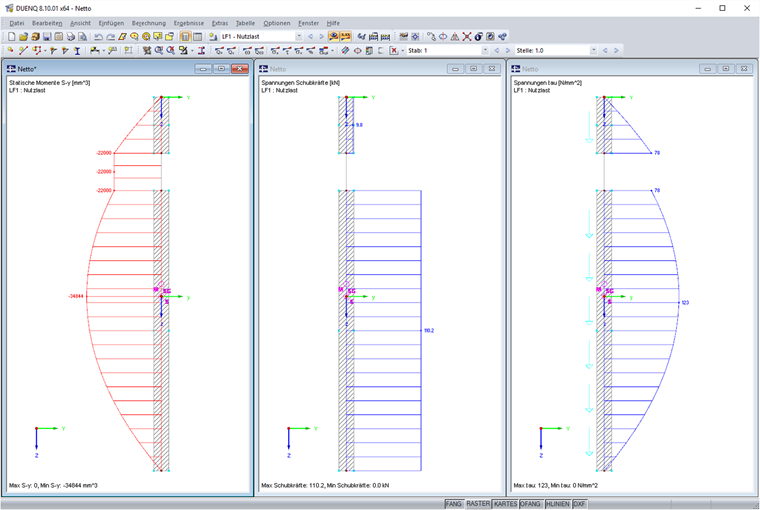
Im nächsten Schritt wird nun das mittlere Element der Länge 20 mm in ein Nullelement umgewandelt. Dies entspricht der oben erwähnten Bohrung. Das Flächenträgheitsmoment ergibt sich zu Iy = 469 cm4. Die Schubspannungen des Nullelements sind nun auf die übrigen Elemente umzuverteilen. Dazu wird ein Korrekturfaktor k ermittelt, der das Verhältnis der Querkraft zu den wirksamen Schubkraft-Anteilen beschreibt.
Die Querkraft wird anschließend intern mit diesem Faktor multipliziert:
Q = 120 ∙ 1,11 = 133,2 kN
Mit dieser modifizierten Querkraft werden nun die Schubspannungen am geschwächten Querschnitt berechnet. Es ergeben sich folgende Verläufe für das statische Moment, die Schubkraft und Schubspannung.
Addiert man die Schubkräfte, erhält man wieder die angesetzte Querkraft von 120 kN. Die Anteile aus dem Nullelement wurden vollständig umgelagert.