Příklad výpočtu
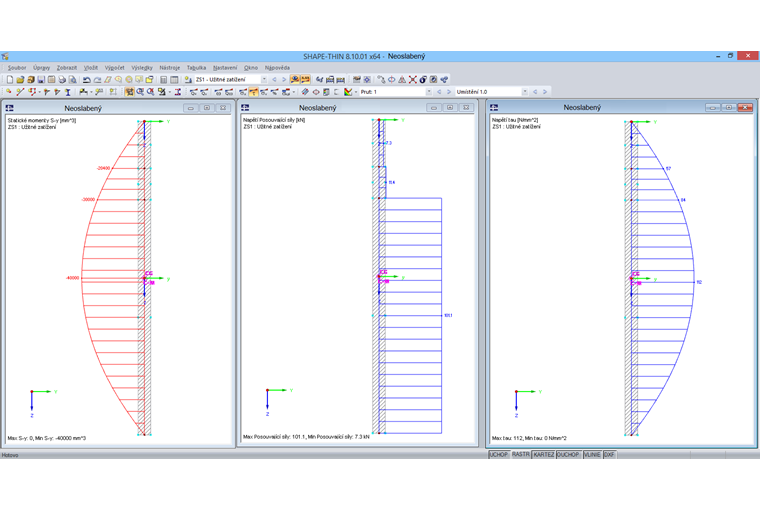
Máme prvek o délce l = 200 mm a tloušťce t = 8 mm, na který bude působit posouvající síla 120 kN, z čehož vyplývají následující průběhy statického momentu, smykové síly a smykového napětí. Výsledný moment setrvačnosti plochy je Iy = 533 cm4.
Smyková síla se přitom stanoví vynásobením smykového napětí délkou a šířkou příslušného prvku. Integrál lze zapsat následovně:
kde z je hodnota souřadnice z.
Jestliže sečteme všechny tři smykové síly, které vyplývají ze zvoleného rozdělení prvku, dostaneme posouvající sílu 120 kN.
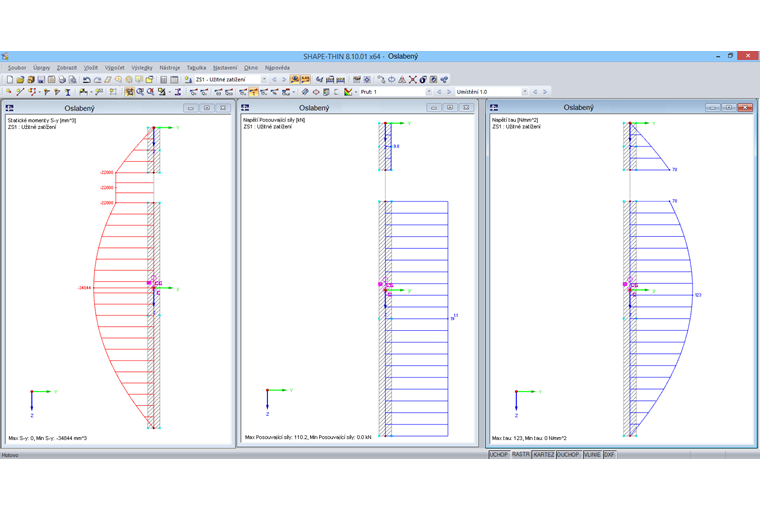
V následujícím kroku převedeme prostřední prvek o délce 20 mm na nulový prvek, který bude odpovídat výše zmíněnému otvoru. Moment setrvačnosti plochy je Iy = 469 cm4. Smyková napětí nulového prvku je nyní třeba přerozdělit na ostatní prvky. Proto vypočítáme opravný součinitel k, který udává poměr posouvající síly a účinných složek smykové síly.
Posouvající síla se následně vynásobí interně tímto součinitelem:
Q = 120 ∙ 1,11 = 133,2 kN
Na základě takto upravené posouvající síly nyní spočítáme smyková napětí na oslabeném průřezu. Výsledkem jsou následující průběhy statického momentu, smykové síly a smykového napětí.
Jestliže sečteme smykové síly, opět dostaneme uvažovanou posouvající sílu 120 kN. Složky z nulového prvku byly plně přerozděleny.
EN 1993-1-3 
DIN 18800-2 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
