Redistribution des contraintes de cisaillement des objets nuls

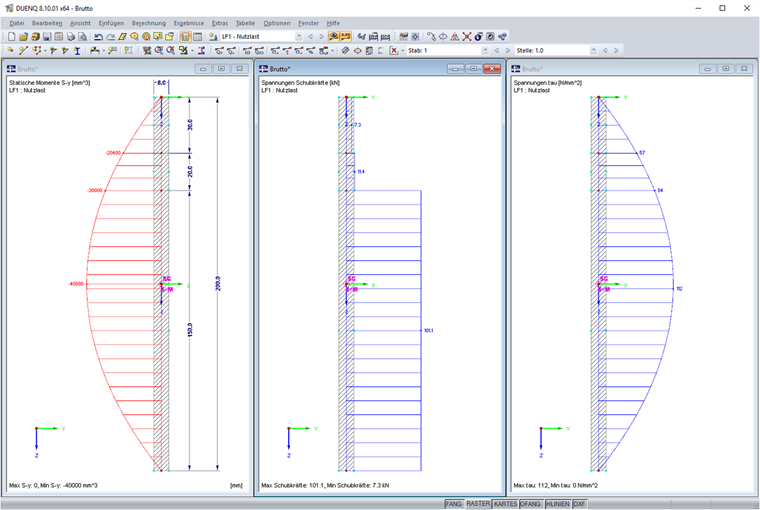
Exemple de calcul

Un élément a une longueur l de 200 mm et une épaisseur t de 8 mm. L’effort tranchant est ici de 120 kN. Il en résulte les distributions suivantes du moment statique, de l’effort tranchant et de la contrainte de cisaillement : Le moment d’inertie résultant est I_y = 533 cm⁴.

Diagramme de résultats de la section brute

L’effort tranchant est ici la contrainte de cisaillement multipliée par la longueur et l’épaisseur de l’élément concerné. L’intégrale est calculée comme suit :

z étant la valeur de la coordonnée z.

Après avoir additionné trois efforts résultant de la division des éléments, on obtient un effort tranchant de 120 kN.

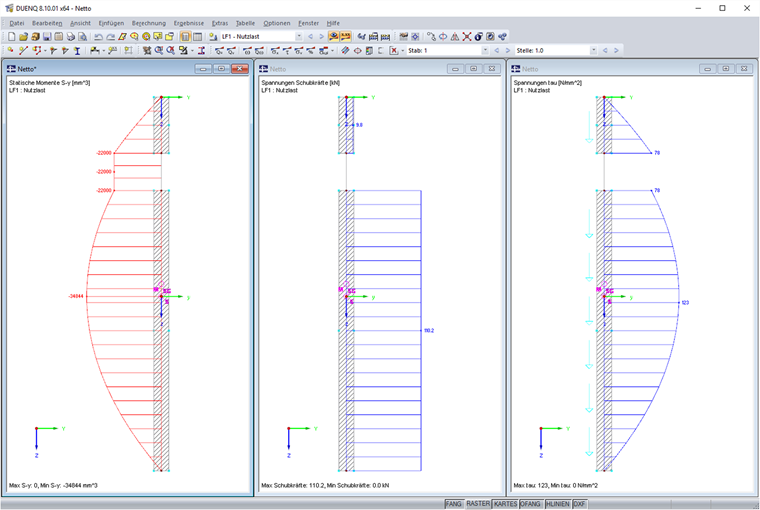
Lors de l’étape suivante, l’élément central de 20 mm de longueur est converti en un élément nul. Cela correspond au trou mentionné ci-dessus. Le moment d’inertie résultant est I_y = 469 cm⁴. Les contraintes de cisaillement de l’élément nul doivent maintenant être réparties sur les autres éléments. Pour cela, un facteur de correction k, qui décrit le rapport des efforts tranchants par rapport aux composants de l'effort tranchant efficace, est déterminé.

L’effort tranchant est ensuite multiplié par ce facteur :
Q = 120 ∙ 1,11 = 133,2 kN

Les contraintes de cisaillement sur la section fragilisée sont alors calculées à l’aide de cet effort tranchant modifié. Les diagrammes suivants sont obtenus pour le premier moment de l’aire, l’effort tranchant et la contrainte de cisaillement.

Diagramme de résultats de la section brute affaiblie

En ajoutant les efforts tranchants, on obtient à nouveau un effort tranchant efficace de 120 kN. Les composants de l’élément nul ont été entièrement redistribués.

Littérature