Example Calculation
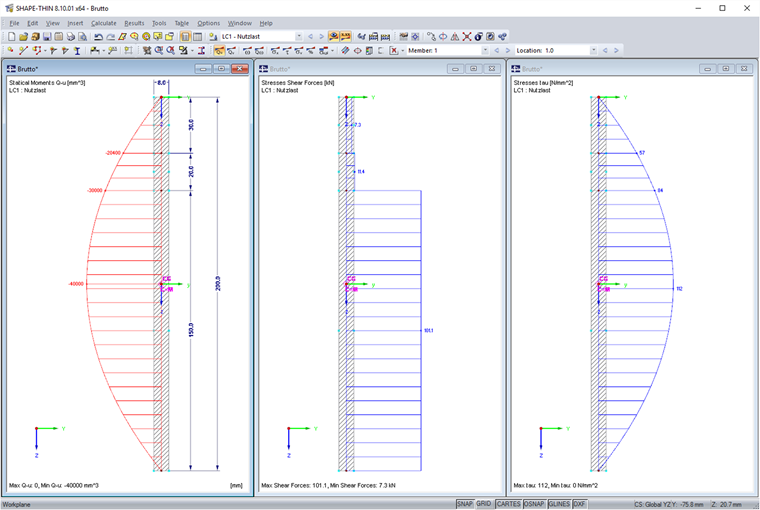
An element has the length l of 200 mm and the thickness t of 8 mm. The shear force is set to 120 kN. This results in the following distributions of the static moment, shear force, and shear stress. The resulting second moment of area is Iy = 533 cm4.
In this case, the shear force is the shear stress multiplied by the length and the thickness of the respective element. The integral is calculated as follows:
where
z is the value of the z-coordinate.
By adding three forces resulting from the division of the elements, you obtain the shear force of 120 kN.
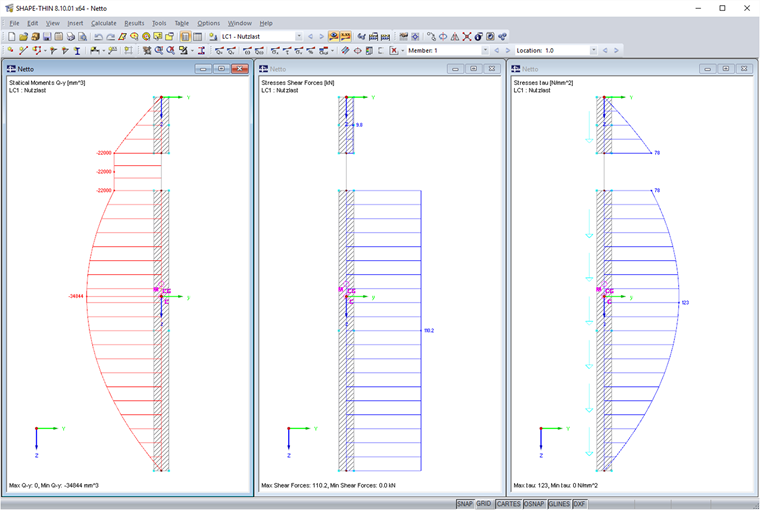
In the next step, the middle element with the length of 20 mm is converted into a null element. This corresponds to the hole mentioned above. The resulting second moment of area results in Iy = 469 cm4. The shear stresses of the null element are now to be distributed to the other elements. For this, a correction factor k is determined, which describes the ratio of the shear force to the effective shear force components.
Then, the shear force is multiplied by this factor:
Q = 120 ∙ 1.11 = 133.2 kN
Using this modified shear force, the shear stresses on the weakened cross-section are now calculated. The following diagrams result for the first moment of area, the shear force and the shear stress.
By adding the shear forces, the effective shear force of 120 kN is obtained again. The null element components were completely redistributed.