13637x

001629

Sonja von Bloh, M.Sc.

2020-03-02

Расчет тонкостенного холодногнутого С-образного профиля по норме EN 1993-1-3

С помощью модульного расширения RF-/STEEL Cold-Formed Sections можно выполнять расчет холодногнутых профилей на предельное состояние по несущей способности согласно норме EN 1993-1-3 и EN 1993-1-5. Тем не менее, кроме холодногнутых профилей из базы данных сечений в нем можно рассчитывать также общие сечения из программы SHAPE-THIN.

В следующем примере из сборника Stahlbau-Kalender 2009 [3]] будет выполнен расчет однопролетной балки из тонкостенного холодногнутого С-образного профиля нормальная силовая нагрузка. Это С-образное сечение будет сначала смоделировано в программе SHAPE-THIN, а затем рассчитано в модульном расширении RF-/STEEL Cold-Formed Sections.

Система

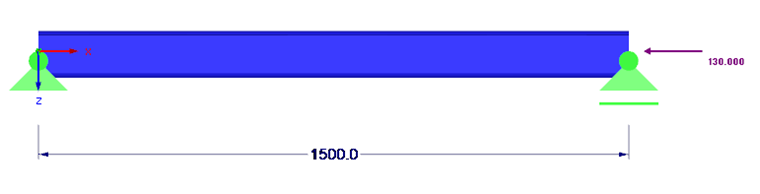
Конструктивная система и нагружение показаны на рисунке 01.

1 Конструктивная система и нагружение (размеры в мм, сила в кН)

Материал

S 355 EN 10025-2
E = 210 000 Н/мм²
G = 80 769 Н/мм²
ν = 0,3
f_y = f_yb = 355 Н/мм²
γ_M0 = γ_M1 = 1,00 (расчет по CEN)

Внешние размеры

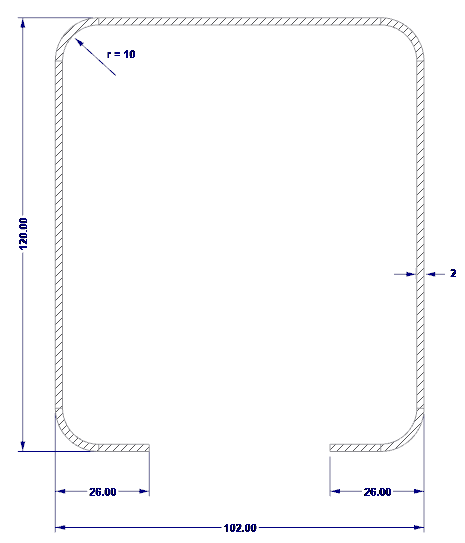
Внешние размеры сечения показаны на рисунке 02.

2 Außenabmessungen des Querschnitts in mm

H = 102 мм (высота стенки)
b = 120 мм (ширина полки)
c = 26 мм (длина кромки)
t = 2 мм (толщина стального сердечника)

Номинальные значения ширины

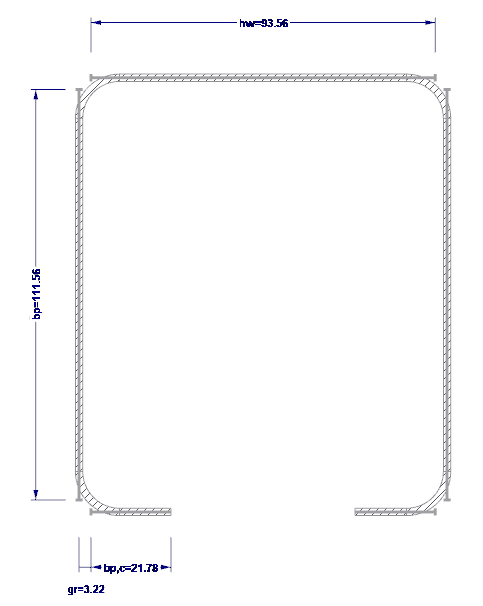
Номинальные значения ширины определяются по {%ref#Refer [1]]], 5.1. Номинальные значения ширины показаны на рисунке 03.

3 Номинальные значения ширины в мм

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Номинальные значения ширины

Проверка соотношений ширины к толщине

Отношение ширины к толщине проверяются по {%><#Refer [1]]], 5.2 (1).

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

Соотношения ширины с толщиной соблюдены.

Проверка размеров элементов жесткости

Размеры элемента жесткости проверяются по [1], 5.2 (2).
0,2 ≤ c/b = 26/120 = 0,22 ≤ 0,6

В качестве элементов жесткости можно применить кромки.

Проверка величины угла между элементом жесткости и плоскостным элементом

Угол между элементом жёсткости и плоскостным элементом составляет 90° в пределах 45° и 135°, указанных в {%|#Refer [1]]], 5.5.3.2(1).

Расчет полезной площади сечения

У стальных профилей, не обладающих двойной симметрией, находящихся под действием сжатия и подверженных локальному выпучиванию, положение центра тяжести эффективного сечения смещено по сравнению c сечением брутто. Внешняя сжимающая сила, действующая на сечение брутто центрально, действует на эффективное сечение внецентренно, благодаря чему возникает дополнительный изгибающий момент. Согласно [1] необходимо учитывать дополнительные моменты, возникающие в результате смещения центра тяжести. Поэтому кроме эффективного сечения при простом нагружении сжатием необходимо рассчитать эффективное сечение при простом нагружении изгибом.

Расчет эффективного сечения при простом нагружении сжатием

Коэффициент определяется согласно [2], 4.4 (2) и равен:

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Коэффициент ε

Стенка

Коэффициент потери устойчивости рассчитывается согласно [2], таблица 4.1:

k_{σ} = 4

коэффициент потери устойчивости пластины

Гибкость при продольном изгибе равна:

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Гибкость стенки при потере устойчивости

Коэффициент гибкости выше, чем предельное значение 0,673 согласно {%://#Refer [2]]], 4.4 (2). Поэтому требуется его уменьшение.

Понижающий коэффициент определяется согласно [2], 4.4 (2) и равен:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Понижающий коэффициент для стенки

Согласно [2], таблица 4.1, полезная высота стенки определяется по [2], таблица 4.1:

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Расчетная высота стенки

Полка с кромочным элементом жесткости

На первом этапе определяется первоначальное эффективное сечение элемента жесткости при условии, что кромочный элемент жесткости работает как неподвижная опора и при этом σ_{com, Ed} = f_yb/γ_M0 .

Полка

Коэффициент потери устойчивости рассчитывается согласно [2], таблица 4.1:

k_{σ} = 4

коэффициент потери устойчивости пластины

Гибкость при продольном изгибе равна:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Гибкость при потере устойчивости полки

Понижающий коэффициент определяется согласно [2], 4.4 (2) и равен:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Понижающий коэффициент для полки

Полезная ширина полки согласно [2], таблица 4.1, равна:

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Расчётная ширина полки

крайний элемент жесткости

Коэффициент потери устойчивости рассчитывается согласно [1], 5.5.3.2 (5)

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

значение потери устойчивости кромочного элемента жесткости

Гибкость при продольном изгибе равна:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Гибкость при потере устойчивости кромочного элемента жесткости

Коэффициент гибкости меньше, чем предельное значение 0,748 согласно {%://#Refer [1]]], 4.4 (2). Таким образом, уменьшения не требуется, то есть: ρ = 1,0.

Первое приближение полезной ширины вытекает из {%ref#Refer [1]]], уравнение 5.13a до:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Первый подход к эффективной ширине

На втором этапе определяется понижающий коэффициент для потери устойчивости геометрии сечения с применением первоначального полезного сечения и с учетом действия упругой непрерывной пружинной опоры.

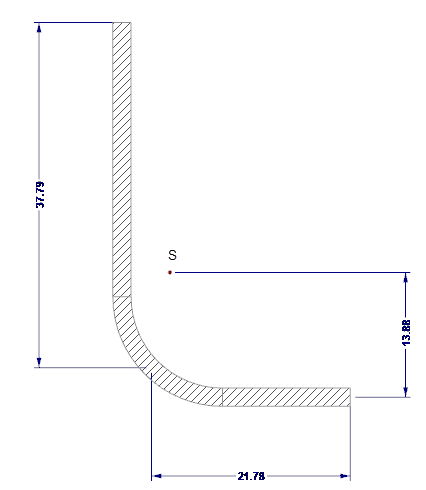
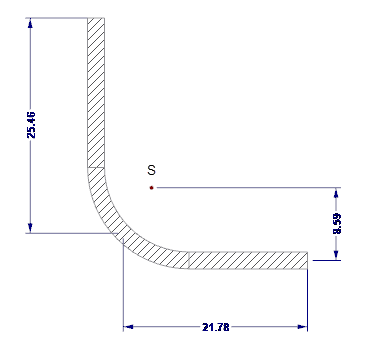
Полезные характеристики сечения кромочных элементов жесткости рассчитываются в программе SHAPE-THIN. Кромочные элементы жесткости показаны на рисунке 04.

4 Эффективные кромочные элементы жесткости

A_s = 122,58 мм²
I_s = 7 130 мм⁴
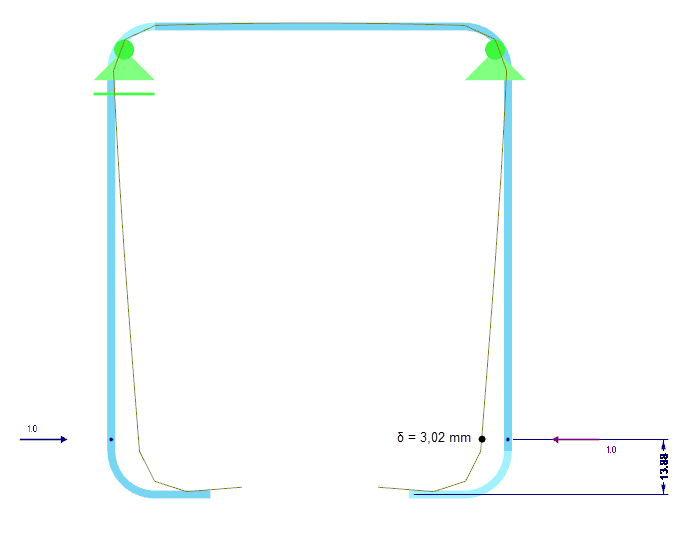
z_s = 13,88 мм

Жесткость пружины K кромок жесткости определяется на основе статического расчета целого сечения. Для этого к сечению будет приложена единичная нагрузка u, действующая в центре тяжести полезного элемента жесткости, а затем рассчитана соответствующая деформация δ элемента жесткости. У прямоугольного сечения w/h = t/t = 2/2 мм деформация равна δ = 3,02 мм (Рисунок 05).

5 Определение жесткости пружины

Жесткость пружины K на единицу длины можно рассчитать по уравнению 5.9 может быть рассчитано следующим образом:

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Жесткость пружины на единицу длины

Критическое напряжение кромочного элемента жесткости определяется по {%ref#Refer [1]]], уравнение 5.15 далее:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Критическое напряжение крайнего элемента жесткости

Коэффициент гибкости рассчитывается по {%ref#Refer [1]]] , уравнение 5.12d до:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Относительный коэффициент гибкости

Согласно [1], 5.5.3.1 (7), понижающий коэффициент для нестабильности формы рассчитывается следующим образом:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

понижающий коэффициент для нестабильности формы

Уменьшенная эффективная площадь сечения кромочного элемента жесткости получена с учетом потери устойчивости при изгибе согласно {%ref#Refer [1]]], уравнение 5.17 до:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Полезная площадь сечения кромочного элемента жесткости

Полезные характеристики сечения при простом нагружении сжатием

Сечение можно оптимизировать с помощью итеративных вычислений. После двух итераций мы получим следующие полезные значения для сечения:

Площадь A_eff = 4,62 см²
Расстояние до центра тяжести от стенки z_{s, eff} = 42,18 мм
Смещение центра тяжести e_N,y = z_s - * z_s,eff = 8,78 мм

Расчет эффективного сечения при простом нагружении изгибом

Стенка

Стенка находится под действием растяжения и, таким образом, полностью эффективна.

Полка с кромочным элементом жесткости

Полка

Коэффициент потери устойчивости рассчитывается согласно [2], таблица 4.1:

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Коэффициент потери устойчивости пояса

Гибкость при продольном изгибе равна:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Гибкость при потере устойчивости полки

Коэффициент гибкости меньше, чем предельное значение 0,856 согласно [2], 4.4 (2). Таким образом, уменьшения не требуется.

Полезные значения ширины согласно [2], таблица 4.1, равны:

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Расчётные ширины пояса

крайний элемент жесткости

Коэффициент потери устойчивости рассчитывается согласно [1], 5.5.3.2 (5)

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

значение потери устойчивости кромочного элемента жесткости

Гибкость при продольном изгибе равна:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Гибкость при потере устойчивости кромочного элемента жесткости

Первое приближение полезной ширины вытекает из {%ref#Refer [1]]], уравнение 5.13a до:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

Первый подход к эффективной ширине

Полезные характеристики сечения кромочных элементов жесткости рассчитываются в программе SHAPE-THIN. Кромочные элементы жесткости показаны на рисунке 06.

6 Wirksamer Steifenquerschnitt

A_s = 97,92 мм²
I_s = 6 271 мм⁴
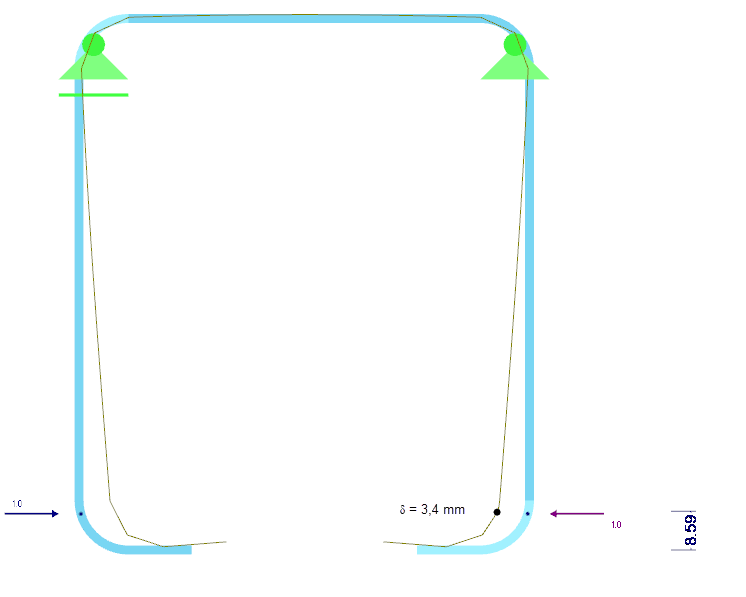
z_s = 8,59 мм

7 Ermittlung der Federsteifigkeit

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Жесткость пружины на единицу длины

Критическое напряжение кромочного элемента жесткости определяется по {%ref#Refer [1]]], уравнение 5.15 далее:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Критическое напряжение крайнего элемента жесткости

Коэффициент гибкости рассчитывается по {%ref#Refer [1]]] , уравнение 5.12d до:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Относительный коэффициент гибкости

Согласно [1], 5.5.3.1 (7), понижающий коэффициент для нестабильности формы рассчитывается следующим образом:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

понижающий коэффициент для нестабильности формы

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Полезная площадь сечения кромочного элемента жесткости

Полезные характеристики сечения при простом нагружении изгибом

Все части сечения полностью эффективны, поэтому не требуются итерационные вычисления.

Площадь A_eff = 6,86 см²
Момент сопротивления сечения W_{eff, y} = 17,01 см³

Расчет сечения при комбинированном нагружении сжатием и изгибом

Сопротивление чистому сжатию рассчитывается по [1], 6.1.3 (1) следующим образом:

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Сопротивление чистому сжатию

Сопротивление чистому изгибу рассчитывается по {%ref#Refer [1]]], 6.1.4.1 (1) следующим образом:

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Чистое сопротивление изгибу

Дополнительный момент, возникающий в результате смещения центра тяжести, определяется по {%ref#Refer [1]]], 6.1.9 (2) следующим образом:

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Дополнительный момент от смещения центра тяжести

Результаты расчета комбинированной нагрузки от сжатия и изгиба по {%ref#Refer [1]]], 6.1.9 (1) равны:

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Расчётная проверка при комбинированной нагрузке от сжатия и изгиба

Расчет выполнен.

Моделирование холодногнутого С-образного профиля в программе SHAPE-THIN

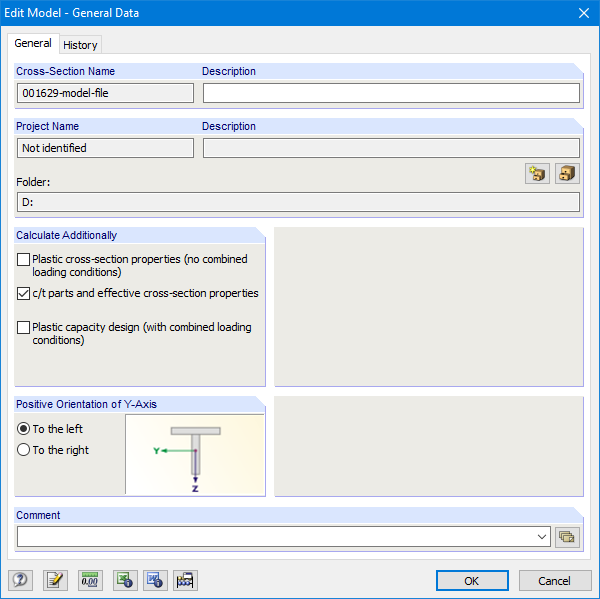
Холодногнутые профили общего типа можно смоделировать в программе SHAPE-THIN. В общих данных нужно активировать флажок «части c/t и полезные характеристики сечения» (Рисунок 08).

8 Основные данные

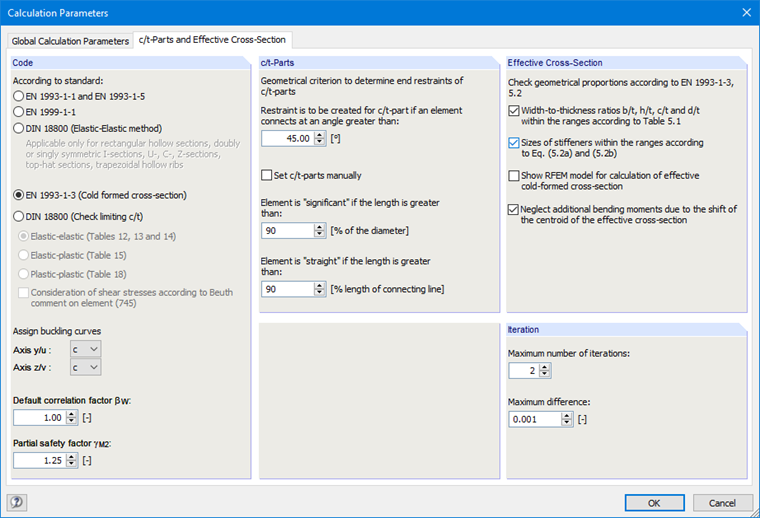
Затем во вкладке «части c/t и эффективное сечение» (рисунок 09) диалогового окна «параметры расчета» выберите параметр «EN 1993-1-3 (холодногнутый профиль)».

Эффективное сечение должно быть рассчитано по отдельности при простом нагружении сжатием и простом нагружении изгибом. Поэтому нужно установить флажок на опцию «пренебречь дополнительными изгибающими моментами вследствие смещения центра тяжести эффективного сечения».

В данном примере был выполнен расчет в две итерации, поэтому в SHAPE-THIN зададим также две итерации.

Дополнительно, можно проверить также геометрические условия применимости нормы, указанные в {%://#Refer [2]]], 5.2. Только не забудьте установить все соответствующие флажки.

9 Параметры расчета

Сначала необходимо задать элементы сечения. Номинальные значения ширины, как правило, генерируются автоматически по геометрическим условиям, но могут также быть заданы пользователем в таблице «1.7 Номинальные значения ширины по норме EN 1993-1-3» (рисунок 10) или в соответствующем диалоговом окне.

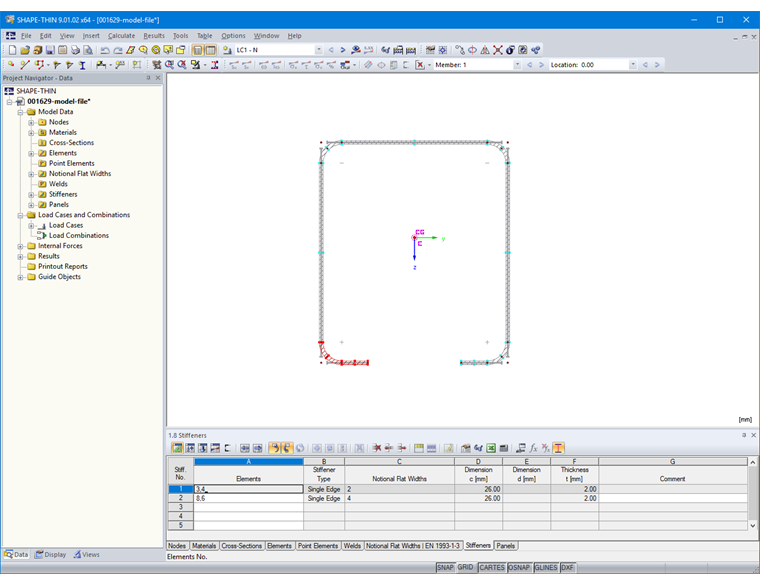
10 Таблица 1.8 Элементы жесткости

Элементы жесткости затем можно задать в таблице «1.8 Элементы жесткости» или в соответствующем диалоговом окне (рисунок 11).

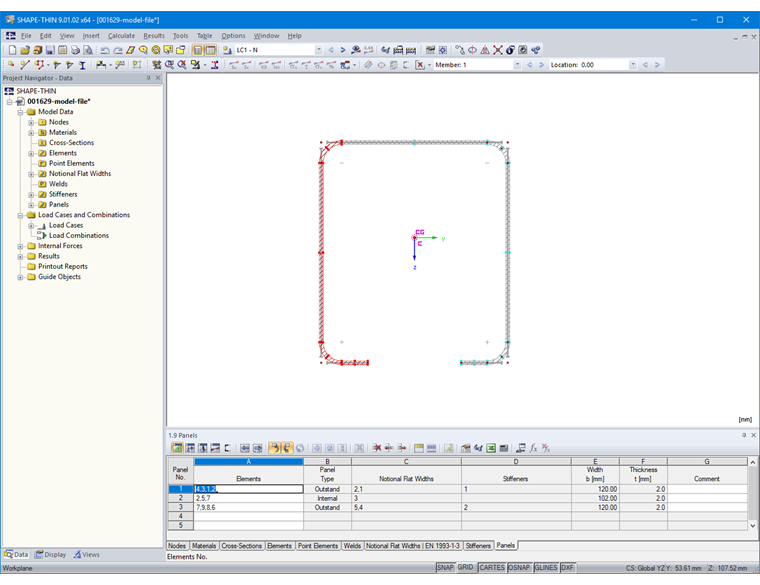
11 Таблица 1.9 Панели

Кроме того, нужно указать теряющую устойчивость панель в таблице «1.9 Панели» (рисунок 12) или в соответствующем диалоговом окне. Однако, для этого нужно сначала выбрать требуемые элементы панели. Элементы жесткости, расположенные в усиленной панели, определяются автоматически.

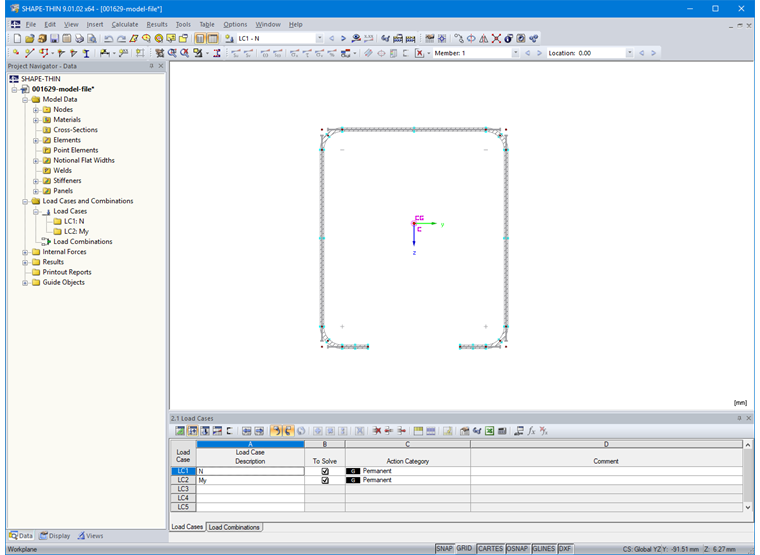
12 Таблица 2.1 Нагружения

Затем в таблице «2.1 Нагружения» зададим нагружение для сжимающей силы и для изгиба (рисунок 13).

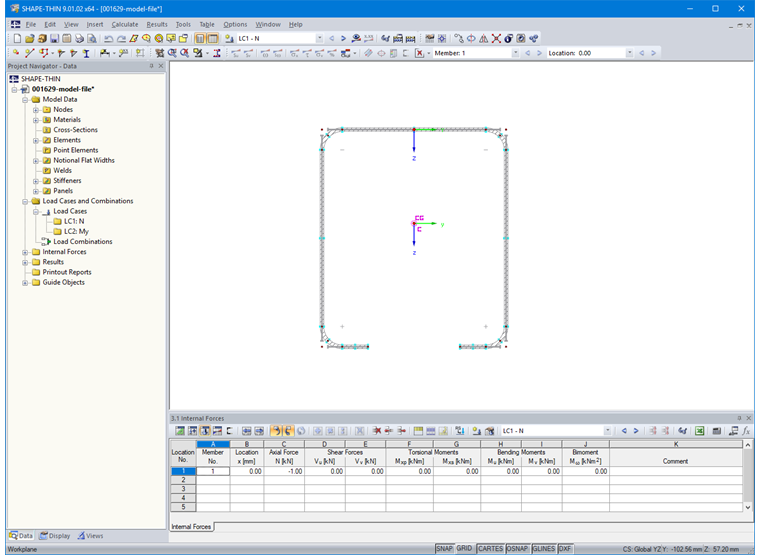
13 Таблица 3.1 Внутренние силы

После этого зададим внутренние силы в таблице «3.1 Внутренние силы» или в соответствующем диалоговом окне (рисунок 14).

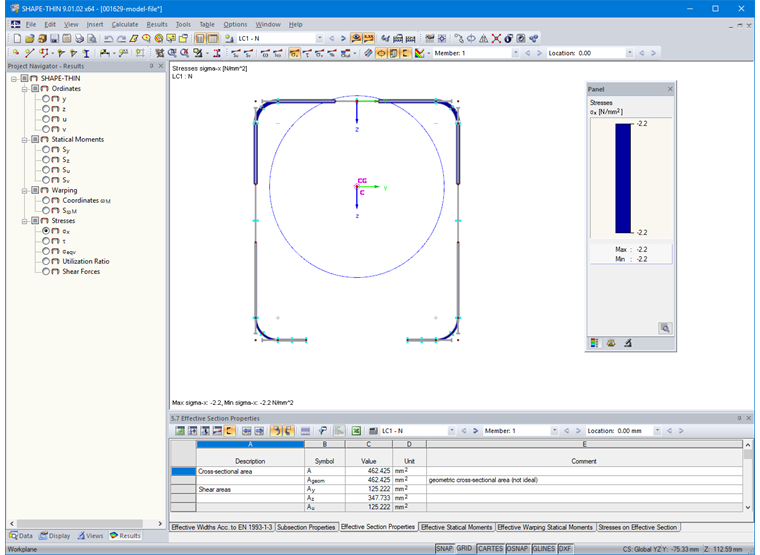
14 Эффективные характеристики сечения

Результаты расчета эффективного сечения можно отобразить с помощью кнопки «Полезные значения ширины» (рисунок 15).

15 Основные данные

Расчет холодногнутого С-образного профиля в RF-/STEEL Cold-Formed Sections

Холодногнутые профили можно рассчитать по {%://#Refer [1]]] и [2] с помощью расширения модуля RF-/STEEL Cold-Formed Sections.

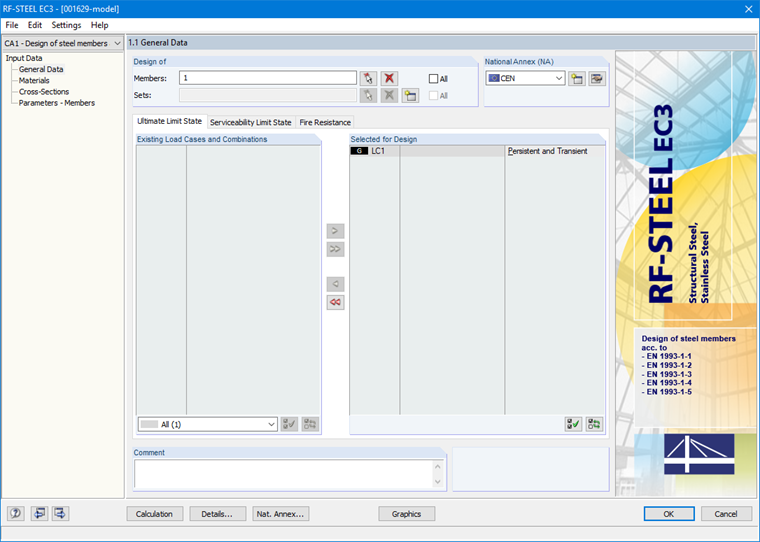
В общих данных необходимо сначала выбрать стержень и нагружение, которые должны быть рассчитаны. В качестве национального приложения выбрано «CEN» (рисунок 16).

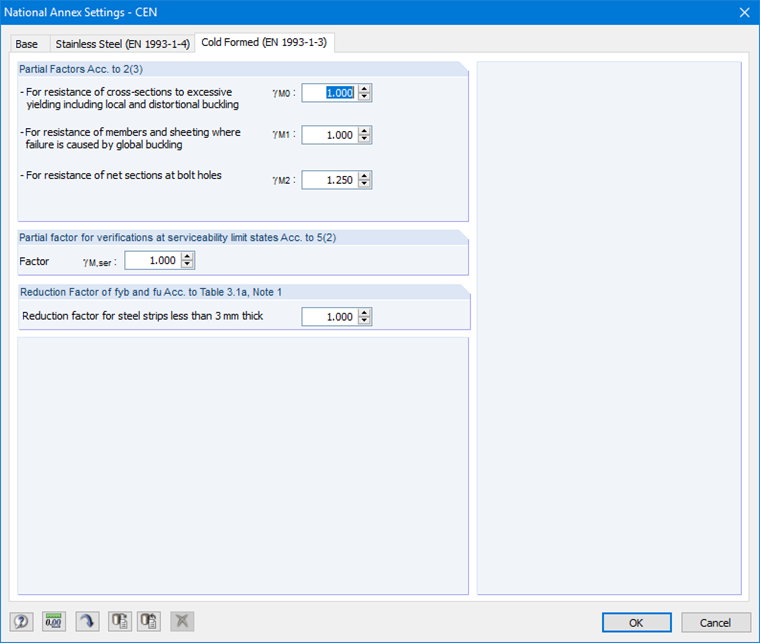
16 Parameter des nationalen Anhangs

Вы можете просмотреть и, при необходимости, отрегулировать параметры национального приложения во вкладке «Холодногнутые профили (EN 1993-1-3)» одноименного окна (рисунок 17).

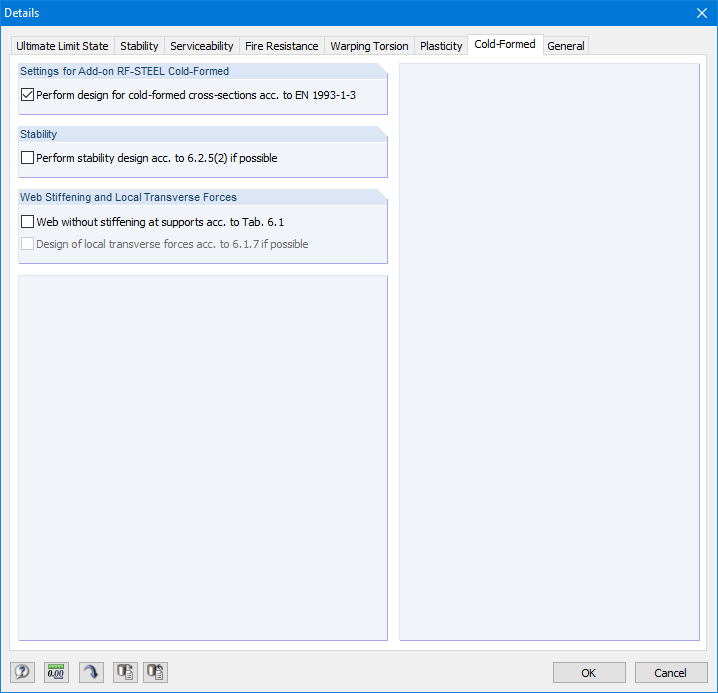
17 Подробности, вкладка «Холодногнутые профили»

В подробных настройках нужно активировать расчет холодногнутых профилей во вкладке «Холодногнутые профили» (рисунок 18).

18 Подробности, вкладка «Устойчивость»

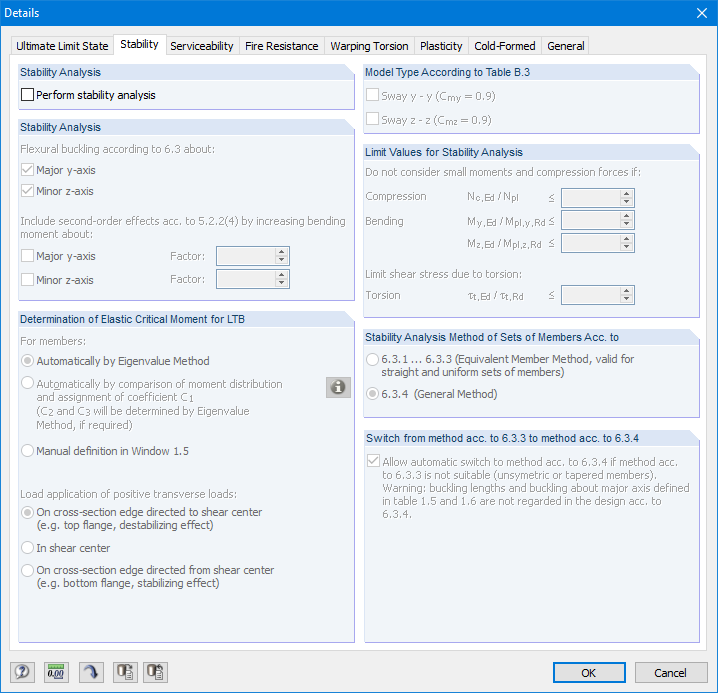
Выполним только расчет сечения. Для этого необходимо деактивировать флажок «Выполнить расчет на устойчивость» во вкладке «Устойчивость» в подробных настройках (рисунок 19).

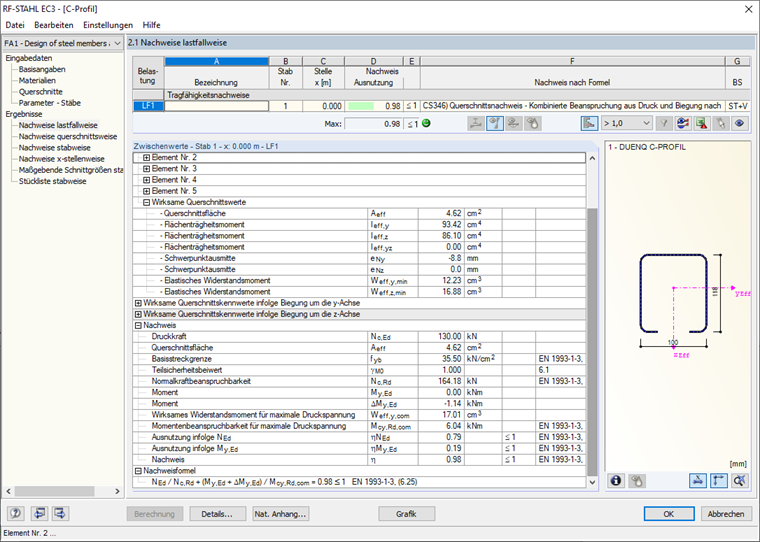
19 Рисунок 20 - Результаты

После выполнения вычислений в соответствующих выходных таблицах, отобразятся, кроме прочего, полезные характеристики сечения при нагружении осевой силой N, изгибающим моментом M_y, изгибающим моментом M_z, внутренние силы и общий расчет (рисунок 20).

20 Таблица 1.7. Условные ширины | EN 1993-1-3

База знаний

KB 001629 | Расчет тонкостенного холодногнутого С-образного профиля по норме EN 1993-1-3

Автор

Г-жа фон Бло оказывает техническую поддержку нашим клиентам и отвечает за разработку программы SHAPE‑THIN, а также стальных и алюминиевых конструкций.

Ссылки

Еврокод 3: Расчет стальных конструкций - Часть 1‑3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Берлин: Beuth, 1993
Еврокод 3: Расчет стальных конструкций - Часть 1-5: Элементы конструкции с покрытием. Издательский дом Beuth GmbH,
Kuhlmann, U .: (2009). Stahlbau-Kalender 2009 - Stabilität, Membantragwerke. Берлин: Ernst & Sohn, 2013

Скачивания

Модель технической статьи | Файл SHAPE-THIN 9

912 KB

Модель технической статьи | Файл RFEM 5

504 KB

Модель технической статьи | Файл RSTAB 8

404 KB

;