13637x

001629

Sonja von Bloh，硕士

2020-03-02

按照 EN 1993-1-3 进行冷弯薄壁 C 型截面设计

使用模块扩展 RF-/STEEL Cold-Formed Sections 可以对冷弯薄壁型钢构件按照欧洲规范 EN 1993-1-3 和 EN 1993-1-5 进行承载能力极限状态设计。除了截面数据库中的冷弯薄壁型钢截面外，您还可以设计由独立程序 SHAPE-THIN 导入的一般截面。

下面的示例选自 2009 年钢结构年鉴{%！轴力荷载在独立程序 SHAPE-THIN 中对该 C 型截面进行建模，然后在模块扩展 RF-/STEEL Cold-Formed Sections 中进行设计。

系统

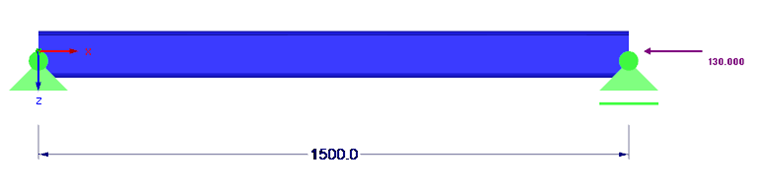
结构体系与荷载如图 01 所示。

1 结构体系与荷载（尺寸单位：mm，力的单位：kN）

材料

S 355 EN 10025-2
E = 210,000 N/mm²
G = 80,769 N/mm²
ν= 0.3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1.00（根据 CEN 设计）

外形尺寸

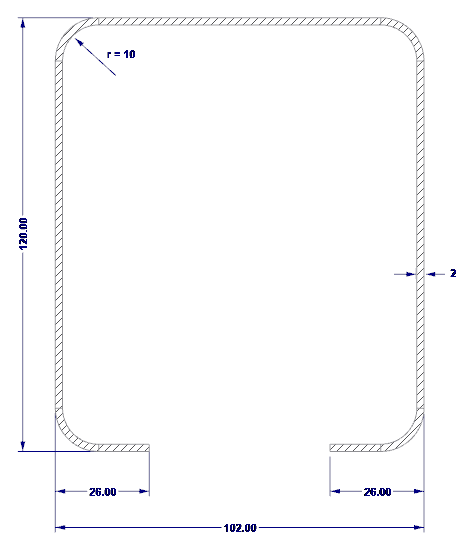
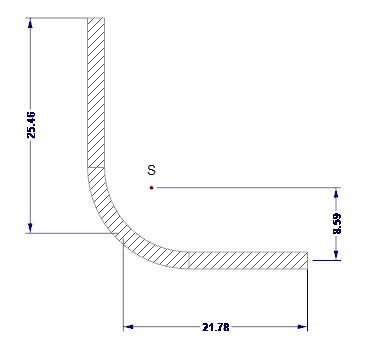
截面的外形尺寸如图 02 所示。

2 Außenabmessungen des Querschnitts in mm

H = 102 mm (腹板高度)
b = 120 mm（翼缘宽度）
c = 26 mm（卷边宽度）
t = 2 mm（截面厚度）

名义平直段宽度

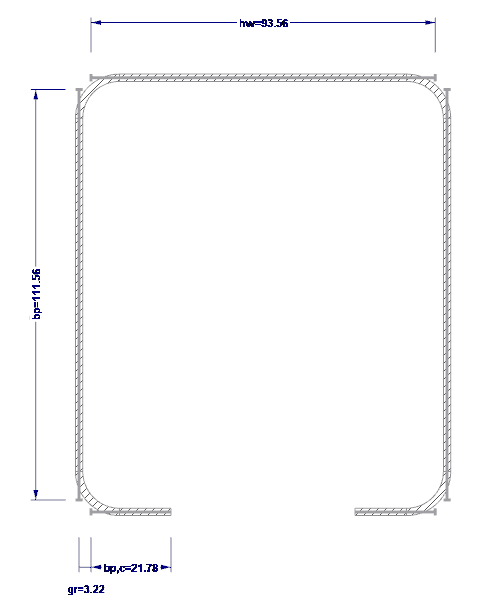
名义平直段宽度按照{%于#参照 [1]]] 中第 5.1 节计算。名义平直段宽度如图 03 所示。

3 名义平直段宽度（单位：mm）

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

名义平直段宽度

检查宽厚比

宽厚比按照 [1] 中 5.2(1) 进行检查。

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

宽厚比满足要求。

检查加劲肋尺寸

加劲肋尺寸按照 [1] 中 5.2(2) 进行检查。
0.2 ≤ c/b = 26/120 = 0.22 ≤ 0.6

卷边可以视为加劲肋。

检查加劲肋与平面单元之间的夹角

加劲肋与平面单元之间的夹角为 90°，位于 5.5.3.2(1) 的 [1] 中提到的 45° 和 135° 之间的范围内。

确定有效截面

对于非双轴对称受压局部屈曲的截面，其有效截面的重心位置相对于毛截面会发生变化。这样作用在毛截面重心位置上的外部压力对于有效截面为偏心作用，同时产生一个附加弯矩。根据 [1] ，必须考虑重心偏移产生的附加弯矩。因此除了计算纯受压作用下的有效截面外，还要计算纯受弯作用下的有效截面。

确定在纯受压作用下的有效截面

根据 {%3}{Refer [2]]] 中 4.4 (2)，系数为：

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

系数 ε

腹板

根据 [2] 中表 4.1，屈曲系数为：

k_{σ} = 4

屈曲值

根据 {%于!#refer [2]]]中的 4.4 (2)，屈曲长细比为：

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

屈曲腹板长细比

根据{%于#参照 [2]]] 中 4.4(2)，长细比大于极限值 0.673。因此需要折减。

根据 [2] 中4.4 (2)，折减系数为：

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

腹板折减系数

根据 {%于#Refer [2]]], 表 4.1，有效腹板高度为：

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

有效腹板高度

有边缘加劲肋的翼缘

第一步假定边缘加劲肋具有完全约束，并且 σ_com,Ed = f_yb / γ_M0，然后确定加劲肋的初始有效截面。

弦杆

根据 [2] 中表 4.1，屈曲系数为：

k_{σ} = 4

屈曲值

根据 {%于!#refer [2]]]中的 4.4 (2)，屈曲长细比为：

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

屈曲翼缘长细比

根据{%于#参照 [2]]] 中 4.4(2)，长细比大于极限值 0.673。因此需要折减。

根据 [2] 中4.4 (2)，折减系数为：

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

翼缘的折减系数

根据表 4.1 中的 {%于#Refer [2]]] ，表 4.1，有效翼缘宽度为：

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

有效翼缘宽度

边缘加劲肋

根据 {%3!#refer [1]]]中 5.5.3.2 (5)，屈曲系数为：

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

边缘加劲肋最大屈曲系数

根据 {%于!#refer [2]]]中的 4.4 (2)，屈曲长细比为：

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

屈曲边缘加劲肋的长细比

根据请参阅{%！因此不需要折减，即 ρ= 1.0。

首次逼近有效宽度的结果参照 {%于#Refer [1]]]，式 24. 5.13a 改为：

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

逼近有效宽度的一阶

第二步使用初始有效截面来确定畸变屈曲的折减系数，同时考虑到连续位移弹簧约束效应。

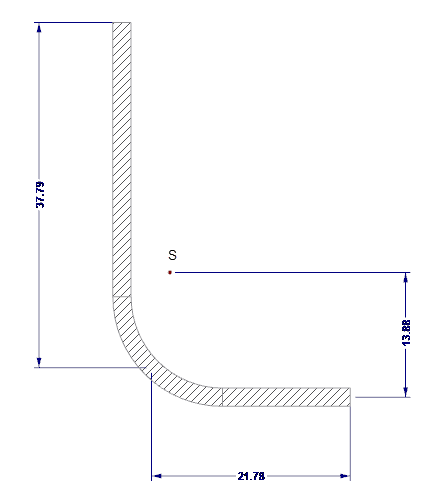
边缘加劲肋的有效截面属性通过 SHAPE-THIN 计算。边缘加劲肋如图 04 所示。

4 有效边缘加劲肋

A_s = 122.58 mm ²
I_s = 7,130 mm ⁴
z_s = 13.88 mm

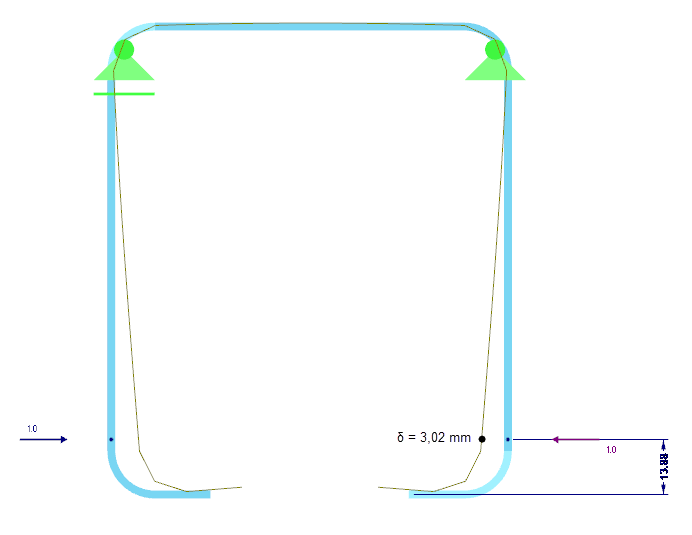
边缘加劲肋的弹簧刚度 K 基于对整个截面的分析来确定。为此在截面上施加一个单位距离荷载 u，该荷载作用于有效加劲肋的重心上，然后计算相应的加劲肋变形 δ。对于矩形截面 b/h = t/t = 2/2 mm，变形δ = 3.02 mm （图 05）。

5 确定弹簧刚度

单位长度的弹簧刚度 K 可根据 {%于#Refer [1]]] 式计算， 5.9 可以按照下式计算：

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

单位长度弹簧刚度

边缘加劲肋的临界应力由公式 11 得出。 5.15 关于：

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

边缘加劲肋的临界应力

长细比按照 {%于#Refer [1]]] 进行计算，公式 24. 5.12d 至：

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

相对长细比

根据{%于#Refer [1]]]中的 5.5.3.1 (7)，畸变屈曲的折减系数为：

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

形状失稳折减系数

考虑弯曲屈曲的影响，边缘加劲肋的折减有效截面面积可按照公式 21.1中的 [1]]] 计算得出。 5.17 至：

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

边缘加劲肋的有效截面面积

纯受压作用下有效截面属性

该截面可以通过迭代计算来优化。通过两步迭代得出以下有效截面属性：

面积 A_eff = 4.62 cm²
腹板的重心距离 z_s,eff = 42.18 mm
重心位移 e_N,y = z_s – * z_s,eff = 8.78 mm

计算在纯弯作用下的有效截面

腹板

腹板受拉，因此全部有效。

有边缘加劲肋的翼缘

第一步假定边缘加劲肋具有完全约束，并且 σ_com,Ed = f_yb / γ_M0，然后确定加劲肋的初始有效截面。

弦杆

根据 [2] 中表 4.1，屈曲系数为：

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

弦杆屈曲系数

根据 {%于!#refer [2]]]中的 4.4 (2)，屈曲长细比为：

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

屈曲翼缘长细比

根据[2] 中 4.4(2)，长细比小于极限值 0.856。因此不需要折减。

根据表 4.1 中的 {%于#Refer [2]]] ，表 4.1，有效宽度为：

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

弦杆有效宽度

边缘加劲肋

根据 {%3!#refer [1]]]中 5.5.3.2 (5)，屈曲系数为：

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

边缘加劲肋最大屈曲系数

根据 {%于!#refer [2]]]中的 4.4 (2)，屈曲长细比为：

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

屈曲边缘加劲肋的长细比

根据请参阅{%！因此不需要折减，即 ρ= 1.0。

首次逼近有效宽度的结果参照 {%于#Refer [1]]]，式 24. 5.13a 改为：

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

逼近有效宽度的一阶

第二步使用初始有效截面来确定畸变屈曲的折减系数，同时考虑到连续位移弹簧约束效应。

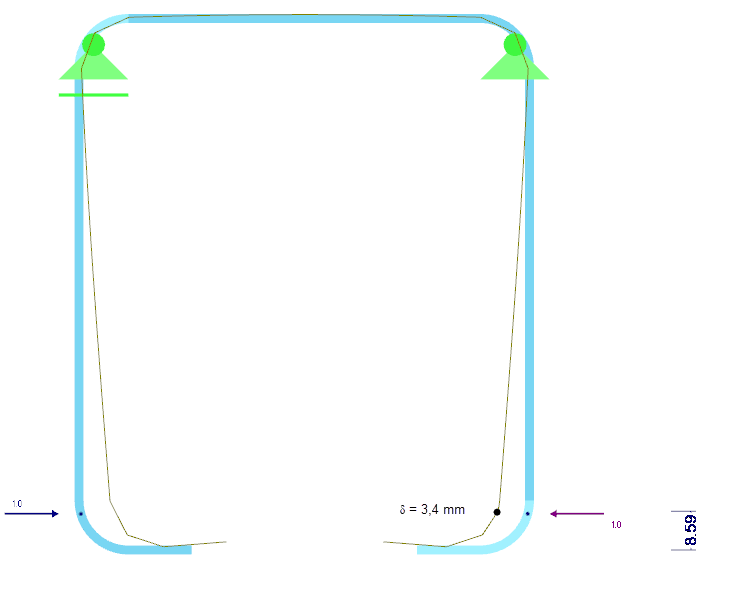
边缘加劲肋的有效截面属性通过 SHAPE-THIN 计算。边缘加劲肋如图 06 所示。

6 Wirksamer Steifenquerschnitt

A_s = 97.92 mm ²
I_s = 6,271 mm ⁴
z_s = 8.59 mm

边缘加劲肋的弹簧刚度 K 基于对整个截面的分析来确定。为此在截面上施加一个单位距离荷载 u，该荷载作用于有效加劲肋的重心上，然后计算相应的加劲肋变形 δ。对于矩形截面 b/h = t/t = 2/2 mm，变形δ = 3.4 mm （图 07）。

7 Ermittlung der Federsteifigkeit

单位长度的弹簧刚度 K 可根据 {%于#Refer [1]]] 式计算， 5.9 可以按照下式计算：

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

单位长度弹簧刚度

边缘加劲肋的临界应力由公式 11 得出。 5.15 关于：

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

边缘加劲肋的临界应力

长细比按照 {%于#Refer [1]]] 进行计算，公式 24. 5.12d 至：

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

相对长细比

根据{%于#Refer [1]]]中的 5.5.3.1 (7)，畸变屈曲的折减系数为：

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

形状失稳折减系数

考虑弯曲屈曲的影响，边缘加劲肋的折减有效截面面积可按照公式 21.1中的 [1]]] 计算得出。 5.17 至：

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

边缘加劲肋的有效截面面积

纯弯曲应力作用下有效截面属性

所有截面部分都是完全有效的，因此不需要迭代。

面积 A_eff = 6.86 cm²
截面模量 W_{eff, y} = 17.01 cm³

压弯截面设计

根据 [1] 中 6.1.3(1)，纯压作用下承载力：

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

纯压承载力

根据 {%于#Refer [1]]] 中 6.1.4.1 (1)，纯弯作用下承载力：

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

纯弯矩承载力

根据[1]中 6.1.9(2) 的规定，重心偏移产生的附加弯矩计算如下：

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

重心偏移产生的附加弯矩

按照 6.1.9 (1) 中有关压弯荷载的设计，请参阅 [1]，

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

压弯荷载共同作用下的设计验算

设计完成。

在 SHAPE-THIN 中对冷弯 C 型截面建模

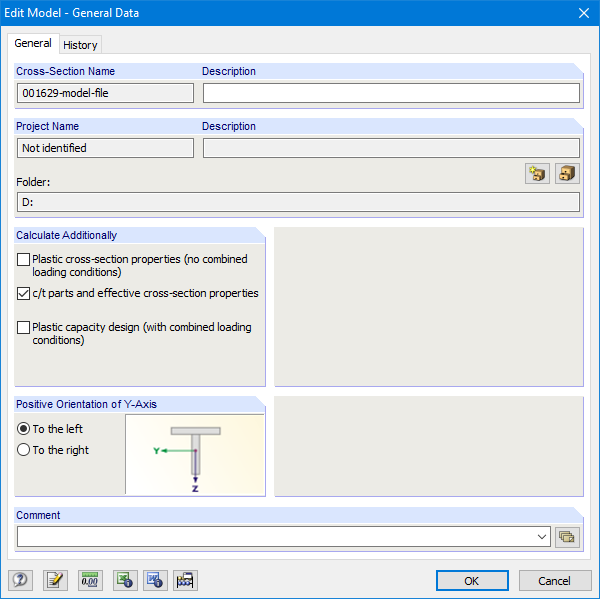
一般的冷弯型材可以在 SHAPE-THIN 中进行建模。在“基本数据”对话框中激活“ c/t 比值和有效截面属性”选项（图 08）。

8 基本数据

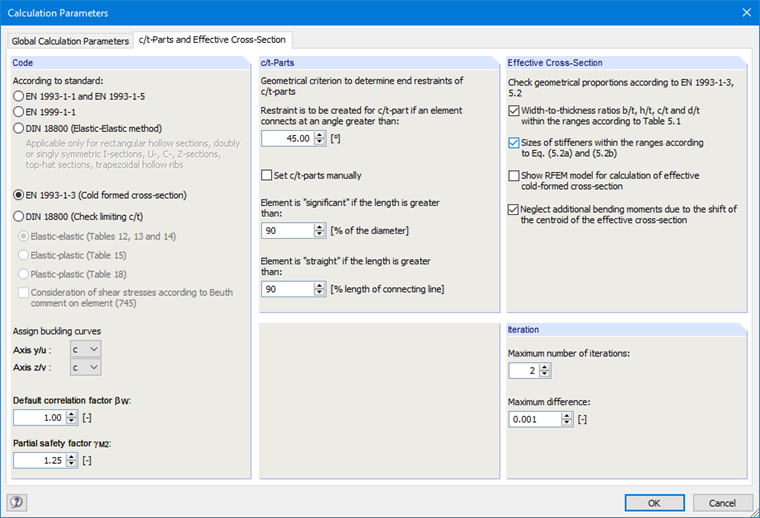
然后在“计算参数”对话框中选择“ c/t 比值和有效截面”选项卡，在该选项卡中选择“ EN 1993-1-3（冷弯截面）”（图09）。

分别计算纯压和纯弯作用下的有效截面。因此需激活“忽略由重心偏移产生的附加弯矩”选项。

该示例计算使用了两步迭代，因此在 SHAPE-THIN 中也设置两步迭代。

可以选择检查第 5.2 节 {%于#Refer [2]]] 中规定的几何尺寸限制条件。为此应激活相应的复选框。

9 计算参数

首先给出截面的单元。通常名义平直段是在几何条件下自动生成，但也可以在表“1.7 名义平直段按 EN 1993-1-3”（图10）或相应的对话框中进行定义。

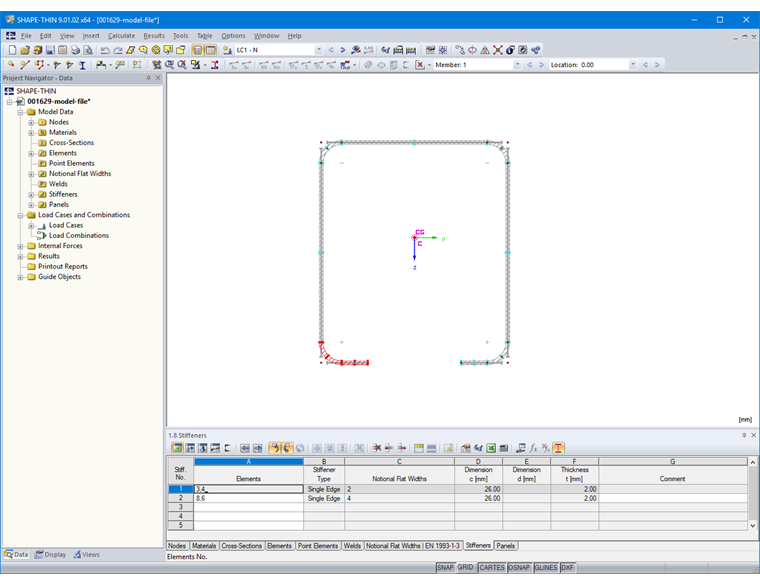
10 表1.8 加劲肋

可以在表“1.8 加劲肋”或相应的对话框中定义加劲肋（图11）。

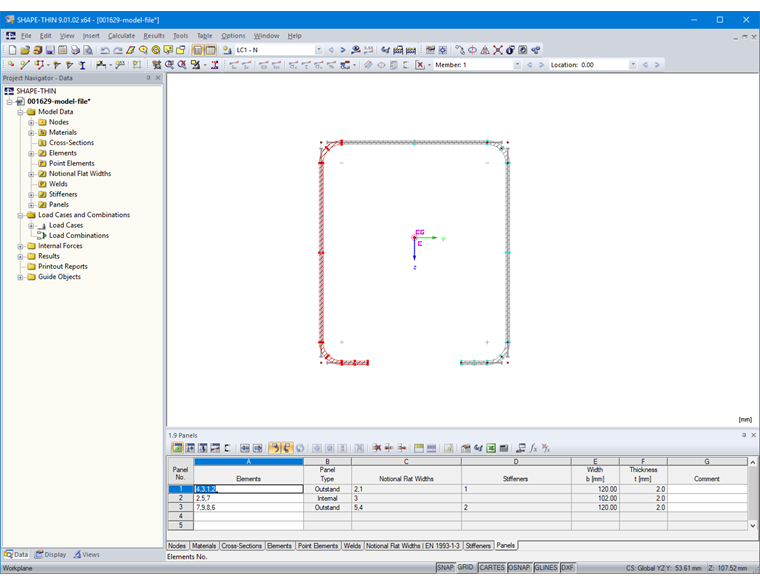
11 表1.9 屈曲区域

此外，在表“1.9 屈曲区域”（图 12）或相应的对话框中指定屈曲区域。为此，请选择屈曲区域的单元。程序会自动识别位于屈曲区域中的加劲肋。

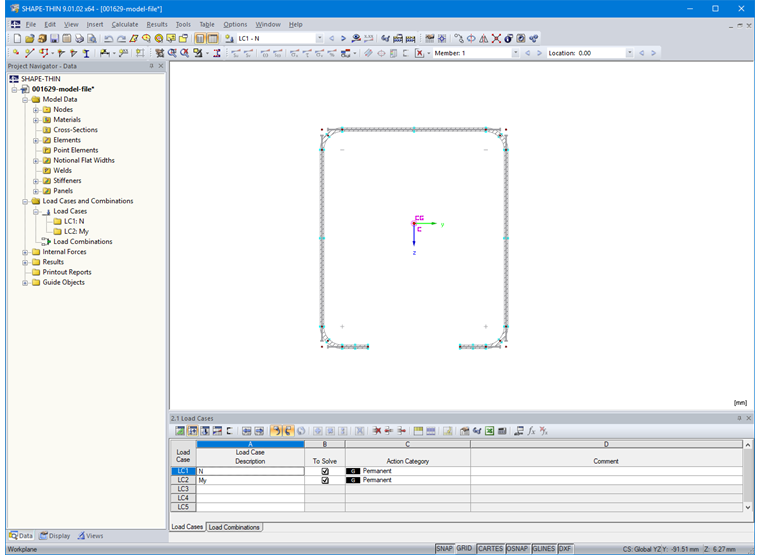
12 表 2.1 荷载工况

此外，在表“ 2.1 荷载工况”中创建受压和受弯荷载工况（图 13）。

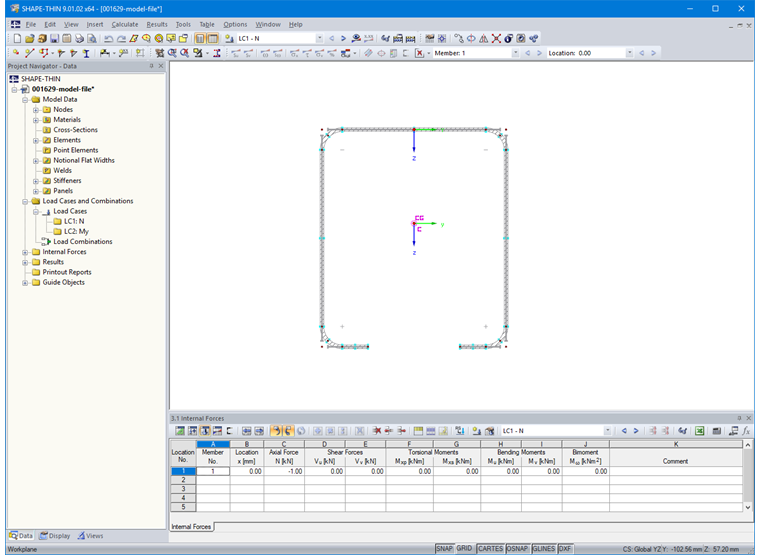
13 表 3.1 内力

然后在表“ 3.1 内力”或相应对话框中输入内力（图 14）。

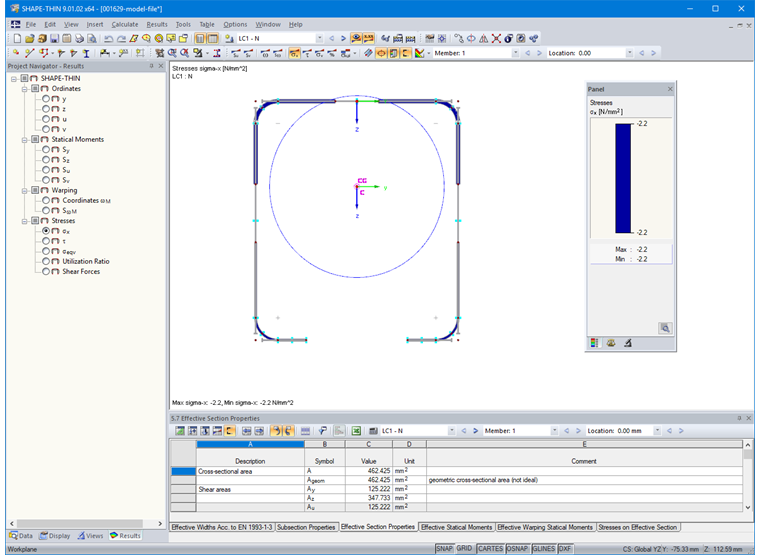
14 有效截面属性

使用按钮“有效宽度”可以查看有效截面的结果。

15 基本数据

RF-/STEEL Cold-Formed Sections 中冷弯 C 型截面设计

冷弯型材可以通过附加模块 RF-/STEEL Cold-Formed Sections 分别按照 [1] 和 [2] 进行设计[SCHOOL.INSTITUTION]

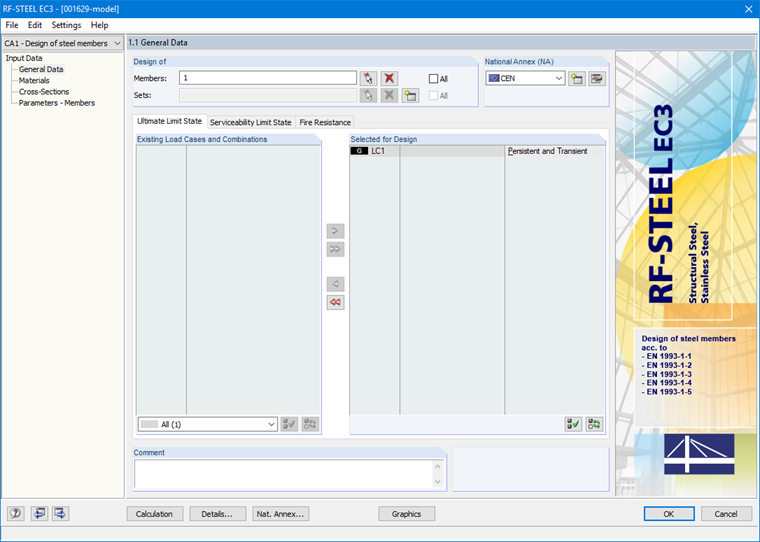
在“基本数据”中必须首先选择要设计的杆件和荷载工况。选择“ CEN” 作为国家附录（图16）。

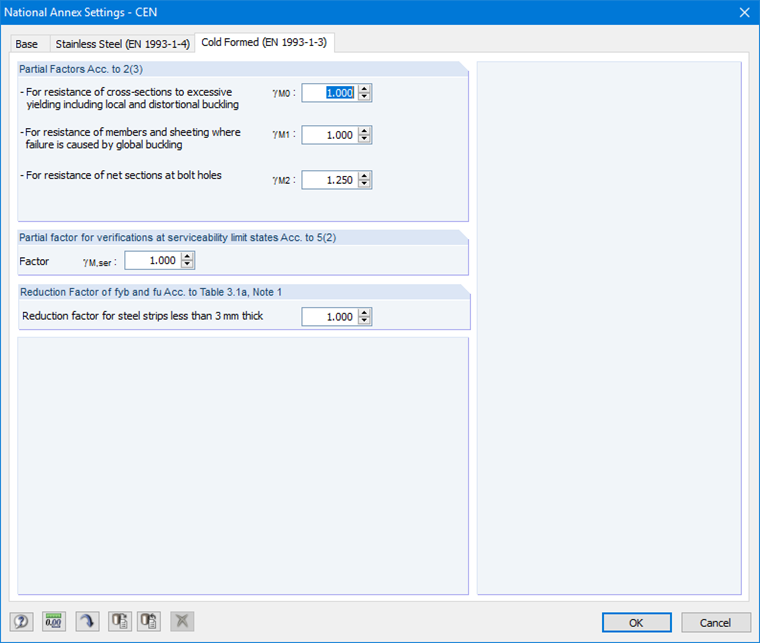
16 Parameter des nationalen Anhangs

您可以在相应窗口的“冷弯型材（EN 1993-1-3）”选项卡中看到并根据需要调整国家附录的参数（图17）。

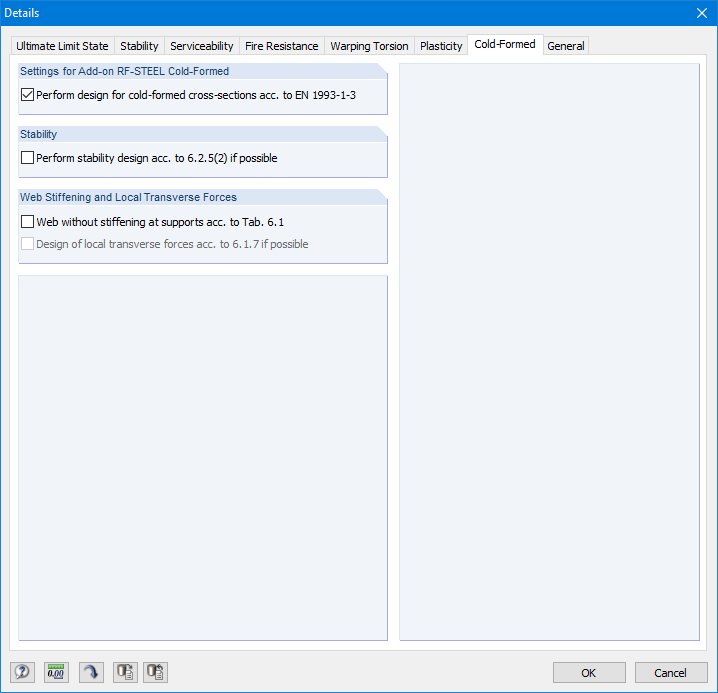
17 详细信息，“冷弯型材”选项卡

在“详细信息”对话框中的“冷弯型材”选项卡里激活冷弯型材验算（图 18）。

18 详细信息，“稳定性”选项卡

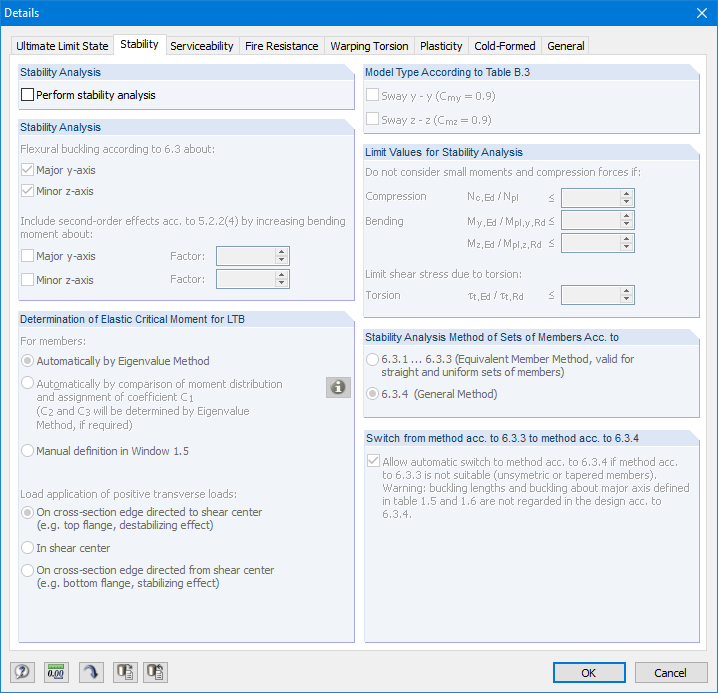
仅进行截面设计。因此必须在“详细信息”对话框中的“稳定性”选项卡里取消激活“进行稳定性验算”选项（图19）。

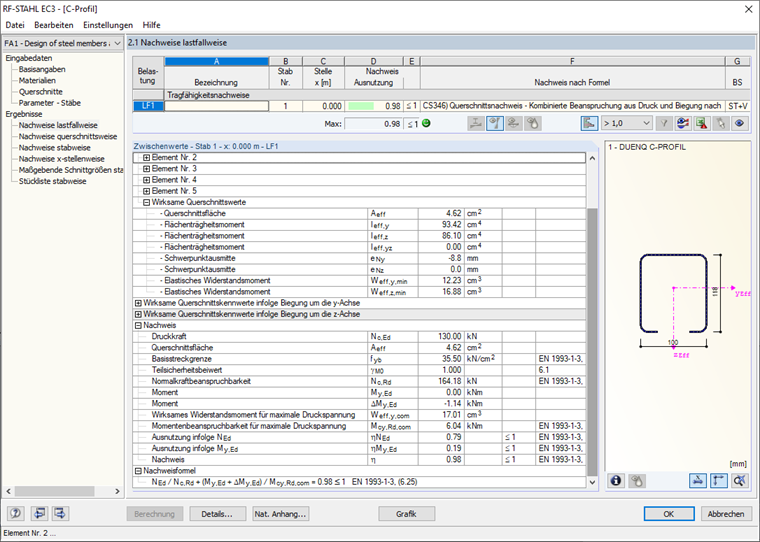
19 图20 -计算结果

计算完成后，在相应的输出表中会显示由轴力 N、弯矩 M_y 和弯矩 M_z计算得出的有效截面属性，以及内力和整个设计（图20）。

20 表1.7 名义平直段宽度 | EN 1993-1-3

知识库

知识库 001629 | 按照 EN 1993-1-3 进行冷弯薄壁 C 型截面设计

作者

von Bloh 女士为我们的客户提供技术支持，负责 SHAPE-THIN 软件的开发，以及钢结构和铝合金结构的开发。

链接

参考

欧洲标准化委员会。 (2010)。欧洲规范 3： Bemessung und Konstruktion von Stahlbauten – Teil 1-3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Beuth Verlag GmbH, Berlin, 2010
EC 3.(2009)。欧洲规范 3：钢结构设计 - 第1-5部分：镀膜结构构件。 Beuth Publishing house GmbH。
库勒曼，U. Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlin: Ernst & Sohn, 2009

下载

技术文章的模型 | SHAPE-THIN 9 文件

;