13737x

001629

Sonja von Bloh, M.Sc.

2.3.2020

Posouzení tenkostěnného C-profilu tvarovaného za studena podle EN 1993-1-3

Profily tvarované za studena lze posoudit na mezní stav únosnosti podle EN 1993-1-3 a EN 1993-1-5 pomocí rozšíření RF-/STEEL Cold-Formed Sections. Posuzovat lze kromě za studena tvarovaných profilů z databáze průřezů také obecné průřezy z programu SHAPE-THIN.

V následujícím příkladu z Ročenky ocelových konstrukcí 2009 [3] se provádí posouzení průřezu prostého nosníku s tenkostěnným C-profilem tvarovaným za studena zatížení normálovou silou. C-průřez modelujeme v programu SHAPE-THIN a následně ho posoudíme v modulu RF-/STEEL Cold-Formed Sections.

Systém

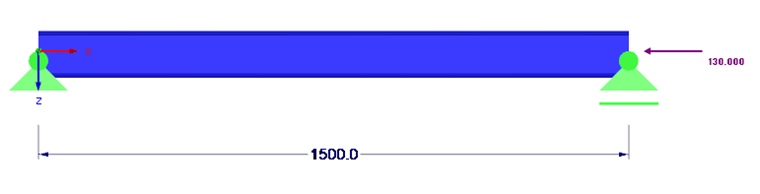
Konstrukce a zatížení jsou znázorněny na obr. 01.

1 Konstrukce a zatížení (rozměry v mm, síla v kN)

Materiál Zdivo

S 355 EN 10025-2
E = 210 000 N/mm²
G = 80 769 N/mm²
ν = 0,3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1,00 (posouzení podle CEN)

Vnější rozměry

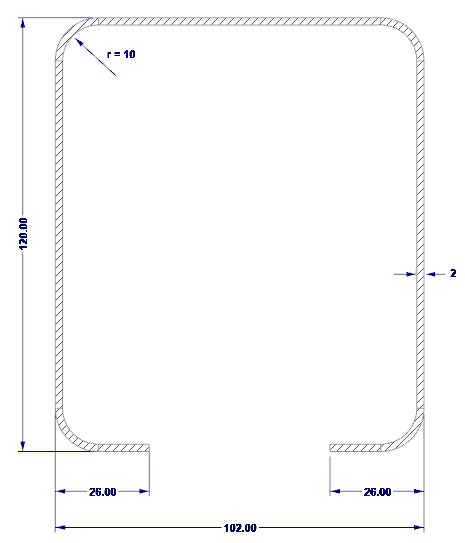
Vnější rozměry průřezu jsou znázorněny na obr. 02.

2 Außenabmessungen des Querschnitts in mm

H = 102 mm (výška stojiny)
b = 120 mm (šířka pásnice)
c = 26 mm (délka jednoduché okrajové výztuhy)
t = 2 mm (tloušťka ocelového jádra)

Výchozí šířky

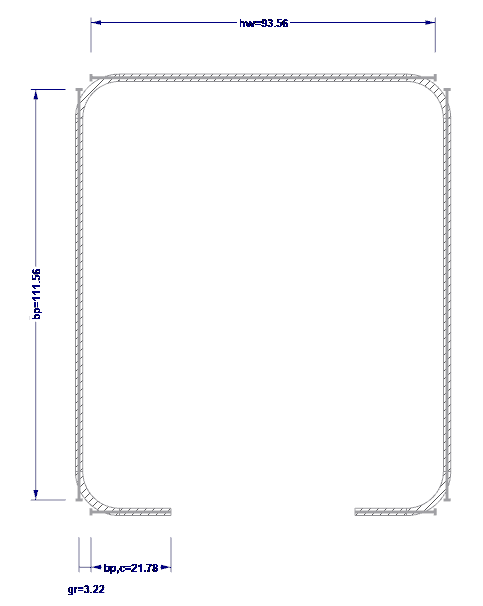
Fiktivní šířky ploch se stanoví podle [1], 5.1. Výchozí šířky jsou znázorněny na obr. 03.

3 Výchozí šířky v mm

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Výchozí šířky

Ověření poměrů šířky ku tloušťce

Poměry šířky k tloušťce se kontrolují podle [1], 5.2(1).

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

Poměry šířky ku tloušťce jsou dodrženy.

Ověření rozměrů výztuhy

Rozměry výztuhy se kontrolují podle [1], 5.2(2).
0,2 ≤ c/b = 26/120 = 0,22 ≤ 0,6

Pro vyztužení lze použít jednoduché okrajové výztuhy.

Ověření úhlu mezi výztuhou a rovinnou částí

Úhel mezi výztuhou a rovinným prvkem je 90° v rozmezí 45° a 135° podle [1], 5.5.3.2(1).

Výpočet účinného průřezu

U ocelových průřezů namáhaných v tlaku, které nejsou dvouose souměrné a jsou náchylné k lokálnímu vyboulení, se poloha těžiště účinného průřezu posouvá ve srovnání s neoslabeným průřezem. Vnější tlaková síla, která působí na neoslabený průřez dostředně, působí na účinný průřez excentricky a vzniká přídavný ohybový moment. Podle [1] je třeba zohlednit přídavné momenty vyplývající z posunu těžiště. Následně je třeba kromě účinného průřezu pro prosté namáhání v tlaku vypočítat také účinný průřez pro prosté namáhání v ohybu.

Výpočet účinného průřezu při prostém namáhání v tlaku

Podle [2], 4.4 (2) je součinitel:

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Součinitel ε

Stojina

Podle [2], tabulky 4.1 je hodnota boulení následující:

k_{σ} = 4

součinitel boulení stěny

Podle [2], 4.4 (2) je štíhlost při boulení následující:

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Štíhlost stojiny při vzpěru

Poměrná štíhlost je větší než mezní hodnota 0,673 podle [2], 4.4(2). Nezbytná je proto redukce.

Podle [2], 4.4 (2) je redukční součinitel:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Redukční součinitel pro stojinu

Účinná výška stojiny se stanoví podle [2], tabulky 4.1 z [2] tabulky 4.1:

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Účinná výška stojiny

Pásnice s okrajovou výztuhou

V prvním kroku se stanoví počáteční účinný průřez výztuhy s použitím účinných šířek určených za předpokladu, že výztuha poskytuje plné podepření a že platí σ_com,Ed = f_yb/γ_M0.

Pás

Podle [2], tabulky 4.1 je hodnota boulení následující:

k_{σ} = 4

součinitel boulení stěny

Podle [2], 4.4 (2) je štíhlost při boulení následující:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Štíhlost při vybočení pásnice

Poměrná štíhlost je větší než mezní hodnota 0,673 podle [2], 4.4(2). Nezbytná je proto redukce.

Podle [2], 4.4 (2) je redukční součinitel:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Redukční součinitel pro pásnici

Podle [2], tabulky 4.1, je účinná šířka pásnice:

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Účinná šířka pásnice

krajní výztuha

Podle [1], 5.5.3.2 (5) je hodnota boulení:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

hodnota boulení okrajové výztuhy

Podle [2], 4.4 (2) je štíhlost při boulení následující:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Štíhlost při vzpěru okrajové výztuhy

Poměrná štíhlost je menší než mezní hodnota 0,748 podle [1], 4.4(2). Žádná redukce tak není zapotřebí, a to znamená: ρ = 1,0.

První přiblížení účinné šířky vyplývá z [1], rovnice 5.13a až:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

První přiblížení účinné šířky

V druhém kroku se určí součinitel vzpěrnosti pro distorzní ztrátu stability za použití počátečního účinného průřezu z prvního kroku a za předpokladu působení spojitého pružného podepření.

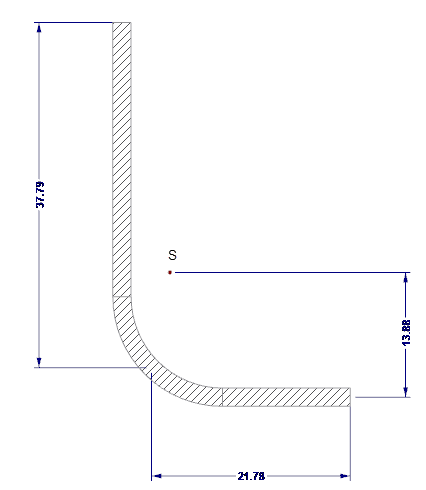
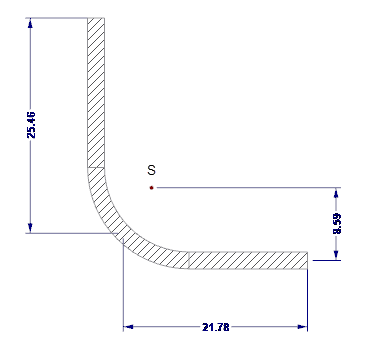
Účinné průřezové hodnoty okrajové výztuhy se spočítají v programu SHAPE-THIN. Okrajová výztuha je znázorněna na obr. 04.

4 Účinná okrajová výztuha

A_s = 122,58 mm²
I_s = 7 130 mm⁴
z_s = 13,88 mm

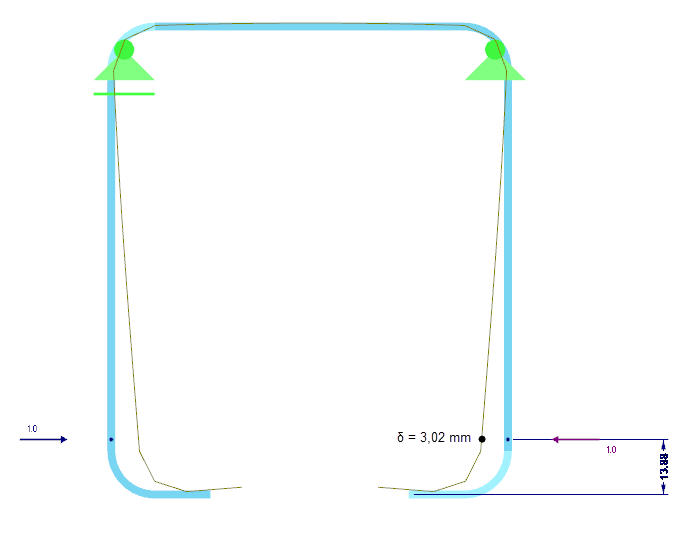
Pérová tuhost K okrajové výztuhy se stanoví na základě statické analýzy celého průřezu. Za tímto účelem se bude na průřezu uvažovat jednotkové zatížení u působící v těžišti účinné výztuhy a vypočítá se příslušná deformace δ výztuhy. Pro obdélníkový průřez w/h = t/t = 2/2 mm je deformace δ = 3,02 mm (obr. 05).

5 Stanovení pérové tuhosti

Tuhost pružiny na jednotku délky K lze vypočítat podle [1], rovnice 5.9 lze vypočítat následovně:

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Tuhost pružiny na jednotku délky

Kritické napětí okrajové tuhosti se stanoví z [1], rovnice 5.15 dne:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Kritické kritické napětí okrajové výztuhy

Poměrná štíhlost se vypočítá podle [1], rovnice 5.12d na:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relativní štíhlost

Podle [1], 5.5.3.1 (7) se redukční součinitel pro tvarovou nestabilitu vypočítá následovně:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

redukční součinitel pro tvarovou nestabilitu

Redukovaná účinná plocha průřezu okrajové tuhosti se stanoví zohledněním rovinného vzpěru podle [1], rovnice 5.17 na:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Účinná průřezová plocha okrajové výztuhy

Účinné průřezové charakteristiky při prostém tlaku

Průřez lze optimalizovat iteračním výpočtem. Při dvou iteracích se stanoví následující účinné průřezové hodnoty:

Plocha A_eff = 4,62 cm²
Vzdálenost těžiště od stojiny z_s,eff = 42,18 mm
Posun těžiště e_N,y = z_s – * z_s,eff = 8,78 mm

Výpočet účinného průřezu při prostém namáhání v ohybu

Stojina

Stojina je namáhána v tahu, a je tak plně účinná.

Pásnice s okrajovou výztuhou

Pás

Podle [2], tabulky 4.1 je hodnota boulení následující:

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Hodnota boulení pásu

Podle [2], 4.4 (2) je štíhlost při boulení následující:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Štíhlost při vybočení pásnice

Poměrná štíhlost je menší než mezní hodnota 0,856 podle [2], 4.4(2). Není tak zapotřebí žádná redukce.

Podle [2], tabulky 4.1 jsou spolupůsobící šířky:

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Účinné šířky pásu

krajní výztuha

Podle [1], 5.5.3.2 (5) je hodnota boulení:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

hodnota boulení okrajové výztuhy

Podle [2], 4.4 (2) je štíhlost při boulení následující:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Štíhlost při vzpěru okrajové výztuhy

Poměrná štíhlost je menší než mezní hodnota 0,748 podle [1], 4.4(2). Žádná redukce tak není zapotřebí, a to znamená: ρ = 1,0.

První přiblížení účinné šířky vyplývá z [1], rovnice 5.13a až:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

První přiblížení účinné šířky

Účinné průřezové hodnoty okrajové výztuhy se spočítají v programu SHAPE-THIN. Okrajová výztuha je znázorněna na obr. 06.

6 Wirksamer Steifenquerschnitt

A_s = 97,92 mm²
I_s = 6 271 mm⁴
z_s = 8,59 mm

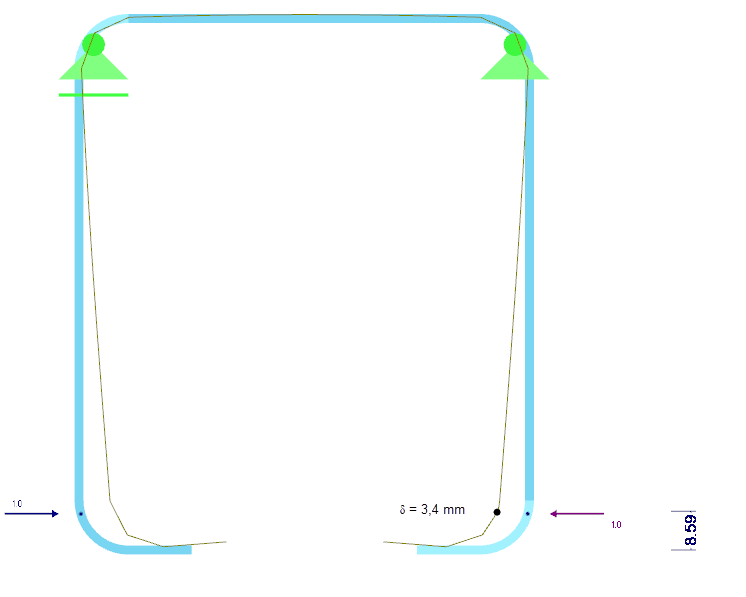
7 Ermittlung der Federsteifigkeit

Tuhost pružiny na jednotku délky K lze vypočítat podle [1], rovnice 5.9 lze vypočítat následovně:

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Tuhost pružiny na jednotku délky

Kritické napětí okrajové tuhosti se stanoví z [1], rovnice 5.15 dne:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Kritické kritické napětí okrajové výztuhy

Poměrná štíhlost se vypočítá podle [1], rovnice 5.12d na:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relativní štíhlost

Podle [1], 5.5.3.1 (7) se redukční součinitel pro tvarovou nestabilitu vypočítá následovně:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

redukční součinitel pro tvarovou nestabilitu

Redukovaná účinná plocha průřezu okrajové tuhosti se stanoví zohledněním rovinného vzpěru podle [1], rovnice 5.17 na:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Účinná průřezová plocha okrajové výztuhy

Účinné průřezové charakteristiky při namáhání prostým ohybem

Všechny části průřezu jsou plně účinné, a není tak nutné přistoupit k iteračnímu výpočtu.

Plocha A_eff = 6,86 cm²
Průřezový modul W_eff,y = 17,01 cm³

Posouzení průřezu za působení v tlaku za ohybu

Únosnost v čistém tlaku se vypočítá podle [1], 6.1.3 (1) následovně:

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Únosnost v čistém tlaku

Únosnost při prostém ohybu se vypočítá podle [1], čl. 6.1.4.1 (1) následovně:

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Únosnost v čistém ohybu

Přídavný moment z posunu těžiště se stanoví podle [1], 6.1.9(2) následovně:

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Přídavný moment od posunu těžiště

Posouzení pro kombinované zatížení od tlaku a ohybu podle [1], 6.1.9 (1) je:

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Posouzení pro kombinované zatížení od tlaku a ohybu

Posouzení je tak splněno.

Modelování C-profilu tvarovaného za studena v programu SHAPE-THIN

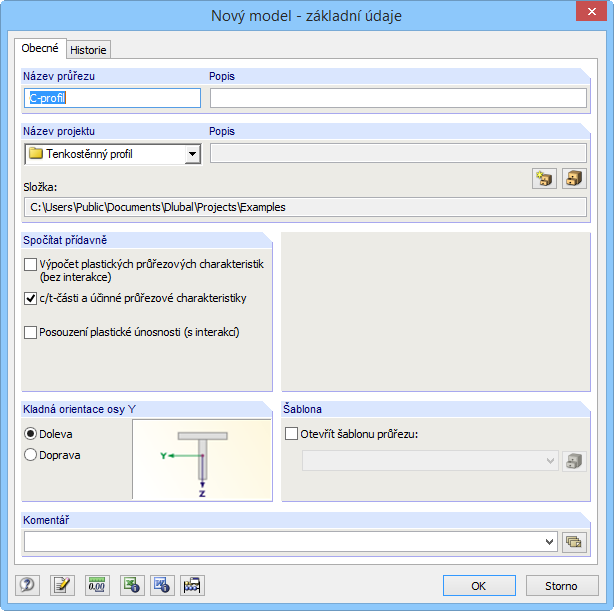
Obecné profily tvarované za studena lze modelovat v programu SHAPE-THIN. V základních údajích je třeba označit políčko „c/t-části a účinné průřezové charakteristiky“ (obr. 08).

8 General Data

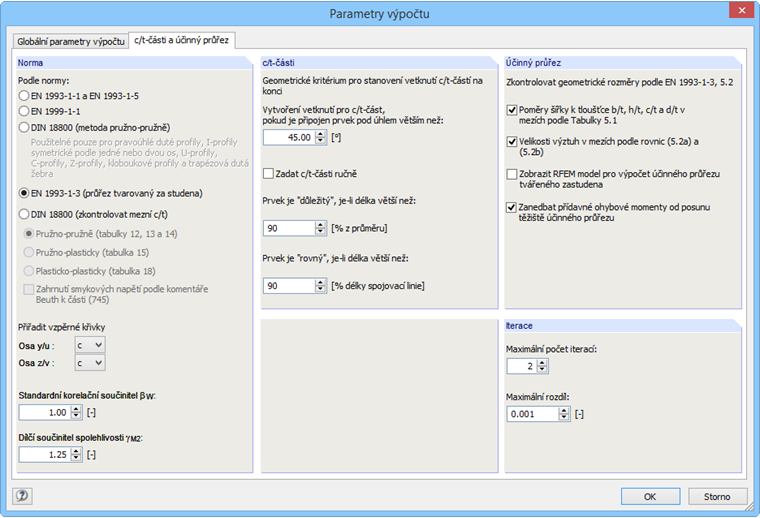
Poté v záložce „c/t-části a účinný průřez“ (obr. 09) v dialogu Parametry výpočtu vybereme možnost „EN 1993-1-3 (průřez tvarovaný za studena)“.

Účinný průřez se stanoví samostatně pro namáhání v prostém tahu a namáhání v prostém ohybu. Proto je třeba zaškrtnout políčko „Zanedbat přídavné ohybové momenty od posunu těžiště účinného průřezu“.

V našem příkladu proběhl výpočet ve dvou iteracích, a proto také v programu SHAPE-THIN nastavíme dvě iterace.

Geometrické podmínky uvedené v [2], 5.2 pro použitelnost normy lze volitelně zkontrolovat. Je třeba označit příslušná zaškrtávací políčka.

9 Parametry výpočtu

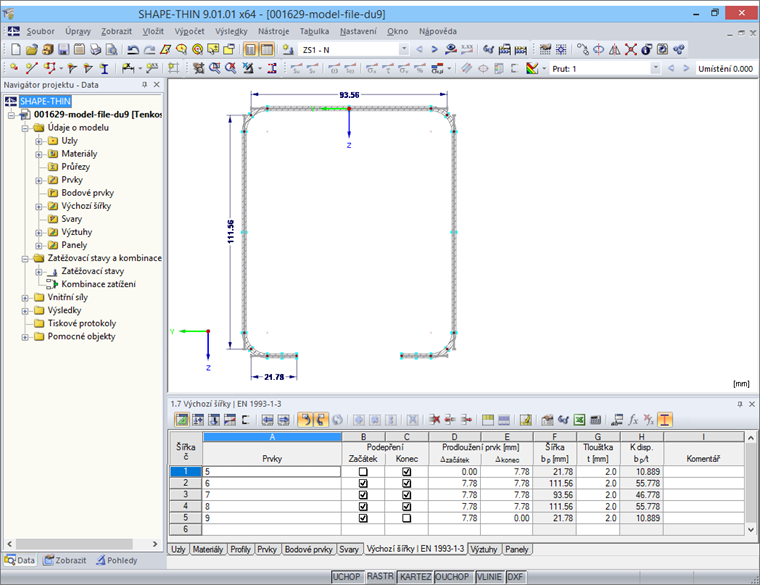
Nejdříve je třeba zadat prvky průřezu. Výchozí šířky se zpravidla automaticky generují z geometrických podmínek, může je ovšem také zadat sám uživatel v tabulce „1.7 Výchozí šířky podle EN 1993-1-3“ (obr. 10) nebo v příslušném dialogu.

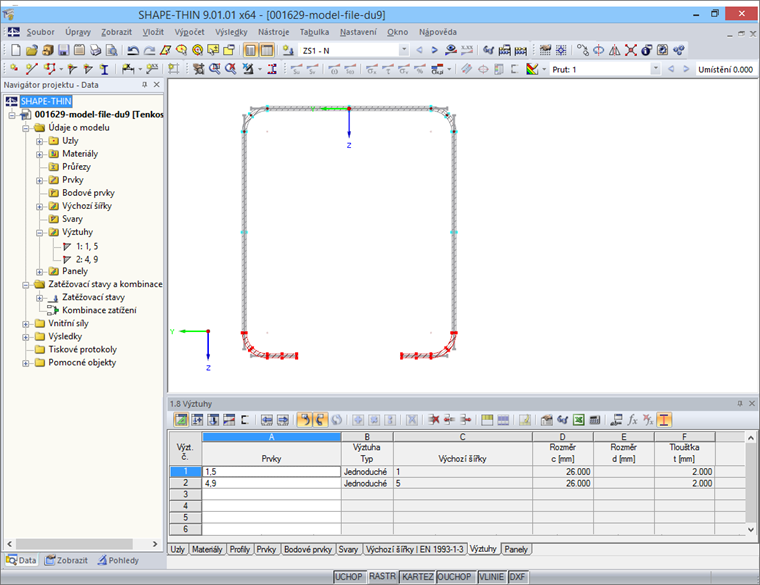
10 Tabulka 1.8 Výztuhy

Výztuhy lze pak zadat v tabulce „1.8 Výztuhy“, případně v odpovídajícím dialogu (obr. 11).

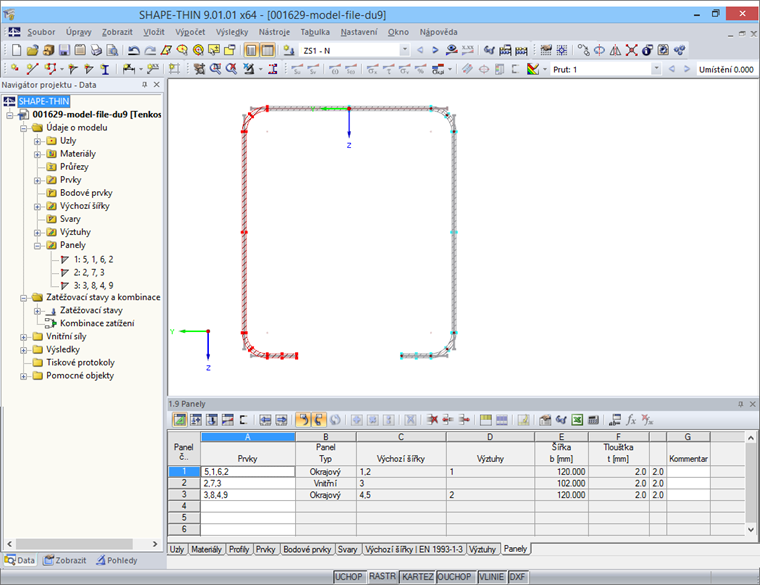
11 Tabulka 1.9 Panely

Dále je pak třeba specifikovat příslušný panel v tabulce „1.9 Panely“ (obr. 12) nebo v odpovídajícím dialogu. Vybereme přitom jednotlivé prvky panelu. Výztuhy v panelu jsou rozpoznány automaticky.

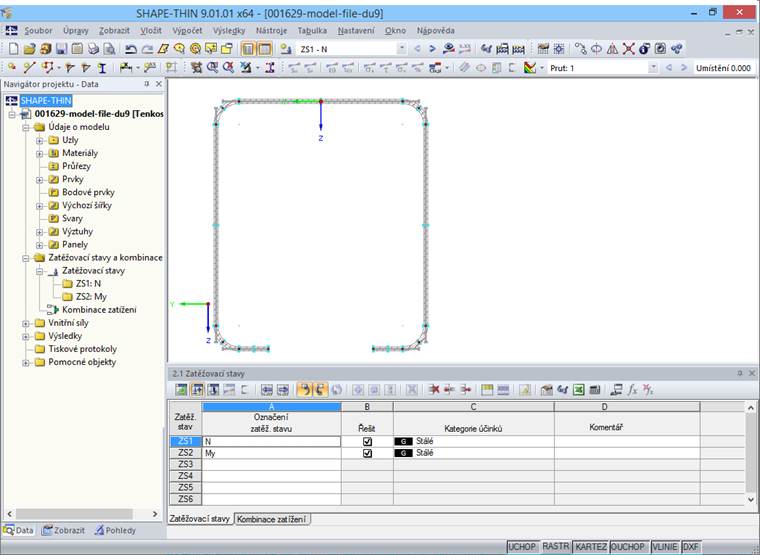
12 Tabulka 2.1 Zatěžovací stavy

V tabulce „2.1 Zatěžovací stavy“ dále vytvoříme jeden zatěžovací stav pro tlakovou sílu a další zatěžovací stav pro ohyb (obr. 13).

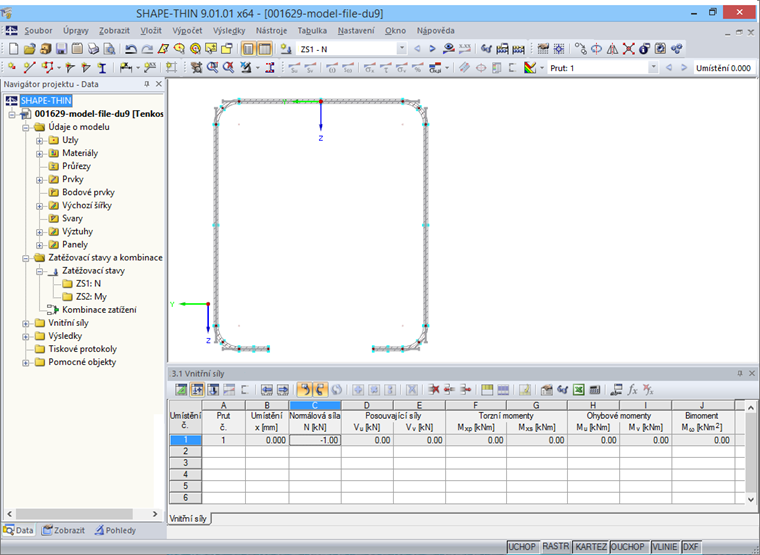
13 Tabulka 3.1 Vnitřní síly

V tabulce „3.1 Vnitřní síly“ nebo v příslušném dialogu následně zadáme vnitřní síly (obr. 14).

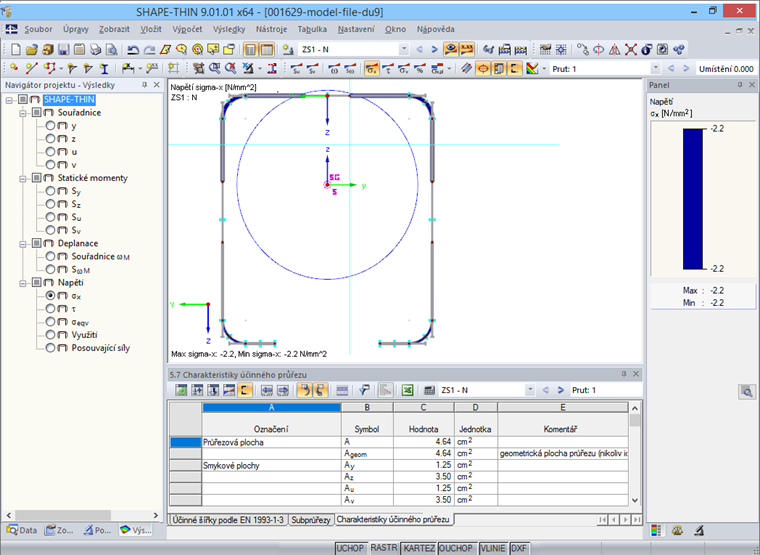
14 Účinné průřezové charakteristiky

Výsledky účinného průřezu se nám zobrazí po kliknutí na „Účinné šířky“ (obr. 15).

15 General Data

Posouzení C-profilu tvarovaného za studena v RF-/STEEL Cold-Formed Sections

Profily tvarované za studena lze posuzovat podle [1] a [2] pomocí přídavného modulu RF-/STEEL Cold-Formed Sections.

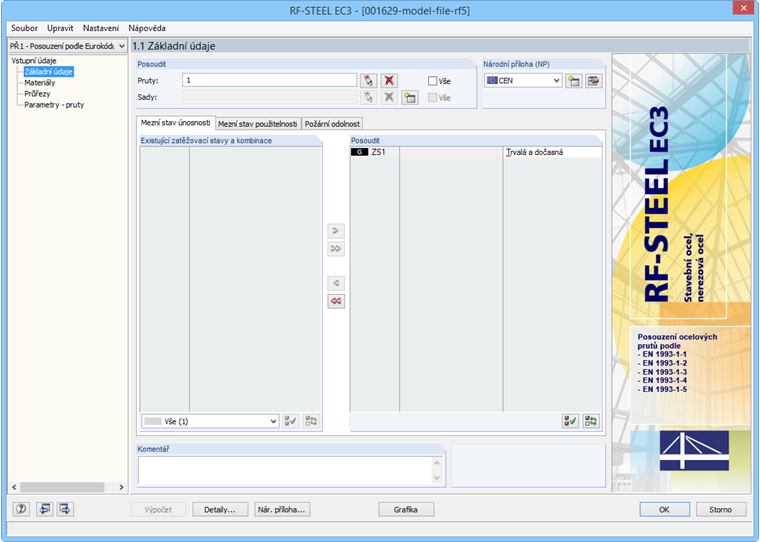
V základních údajích je třeba nejdříve vybrat prut a zatěžovací stav k posouzení. Jako národní přílohu nastavíme „CEN“ (obr. 16).

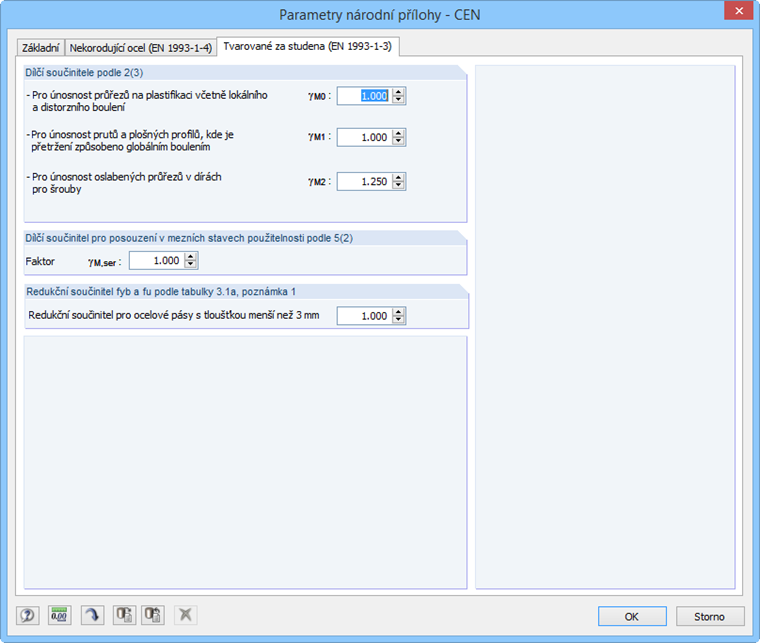
16 Parameter des nationalen Anhangs

Parametry národní přílohy si můžeme prohlédnout a případně upravit v záložce "Tvarované za studena (EN 1993-1-3)" dialogu „Parametry národní přílohy“ (obr. 17).

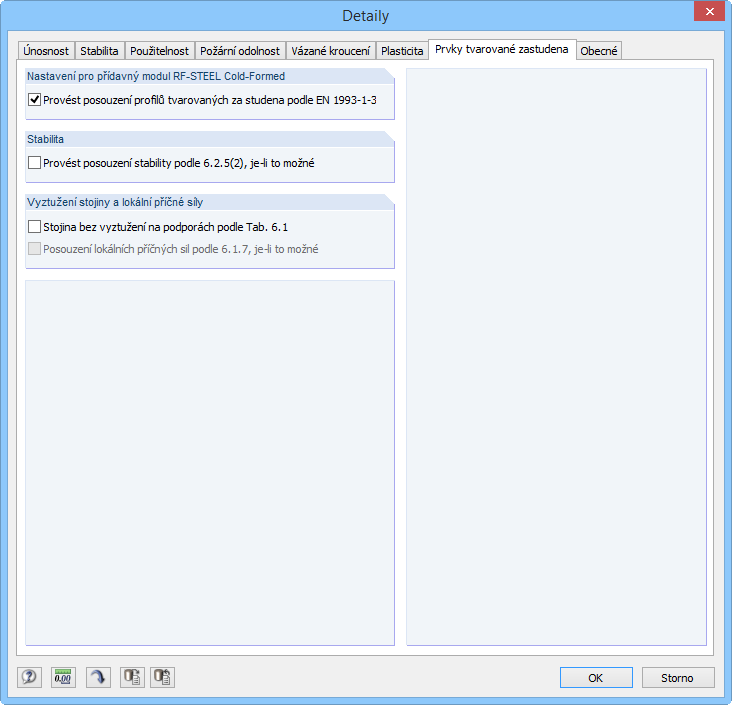
17 Detaily, záložka Prvky tvarované za studena

V detailním nastavení je třeba v záložce „Prvky tvarované za studena“ aktivovat posouzení za studena tvarovaných profilů (obr. 18).

18 Detaily, záložka Stabilita

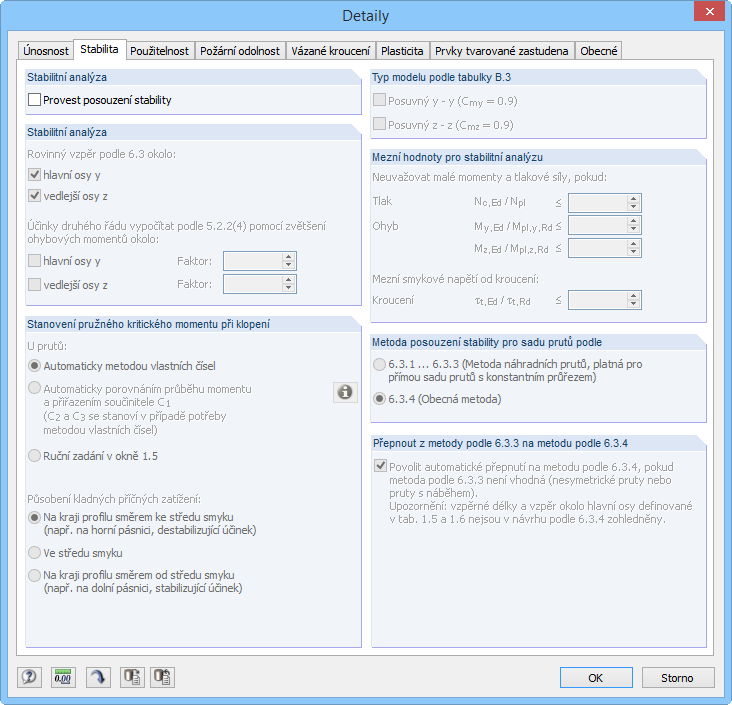
Provedeme pouze posouzení průřezu. Proto je třeba v záložce „Stabilita“ dialogu „Detaily“ zrušit označení políčka „Provést posouzení stability“ (obr. 19).

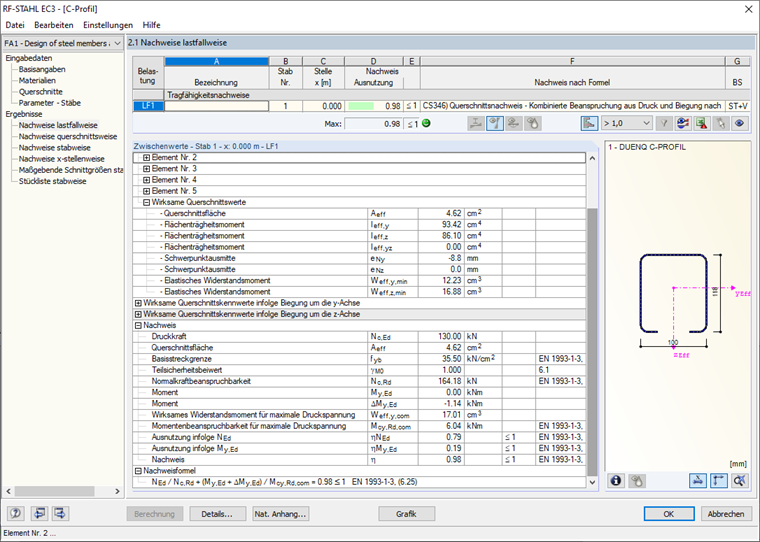
19 Obrázek 20 - Výsledky

Po výpočtu se v příslušných výstupních tabulkách zobrazí mimo jiné účinné průřezové charakteristiky při působení normálové síly N, ohybového momentu M_y, ohybového momentu M_z, dále vnitřní síly a celkové posouzení (obr. 20).

20 Tabulka 1.7 Výchozí šířky podle EN 1993-1-3

Databáze znalostí

KB 001629 | Posouzení tenkostěnného C-profilu tvarovaného za studena podle EN 1993-1-3

Autor

Ing. von Bloh zajišťuje technickou podporu zákazníkům a je zodpovědná za vývoj programu RSECTION a addonů pro ocelové a hliníkové konstrukce.

Odkazy

Reference

Eurokód 3: Navrhování ocelových konstrukcí - Část 1-3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Berlín: Beuth, 2016
Eurokód 3: Navrhování ocelových konstrukcí - Část 1-5: Oplechované konstrukční prvky. Nakladatelství Beuth GmbH.
Kuhlmann, U.: (2009). Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlín: Ernst & Sohn, 2013

Stahování

Model | Soubor SHAPE-THIN 9

912 KB

Model | Soubor RFEM 5

504 KB

Model | Soubor RSTAB 8

404 KB

;