13637x

001629

Sonja von Bloh, M.Sc.

2020-03-02

Design of Thin-Walled, Cold-Formed C-Section According to EN 1993-1-3

Utilize the RF-/STEEL Cold-Formed Sections module extension to perform ultimate limit state design checks of cold-formed sections according to EN 1993-1-3 and EN 1993-1-5. In addition to the cold-formed cross-sections from the cross-section database, you can design general cross-sections from SHAPE-THIN.

In the following example from the Steel Structures Yearbook 2009 [3], the cross-section design for a single-span beam with a thin-walled, cold-formed C-section is performed under normal force loading. The C-section is modeled in SHAPE-THIN and then designed in RF-/STEEL Cold-Formed Sections.

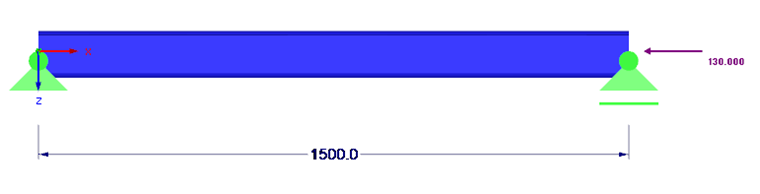
Structural System

System and loading are shown in Image 01.

1 System and Loading (Dimensions in mm, Force in kN)

Material

S 355 EN 10025-2
E = 210,000 N/mm²
G = 80,769 N/mm²
ν = 0.3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1.00 (design according to CEN)

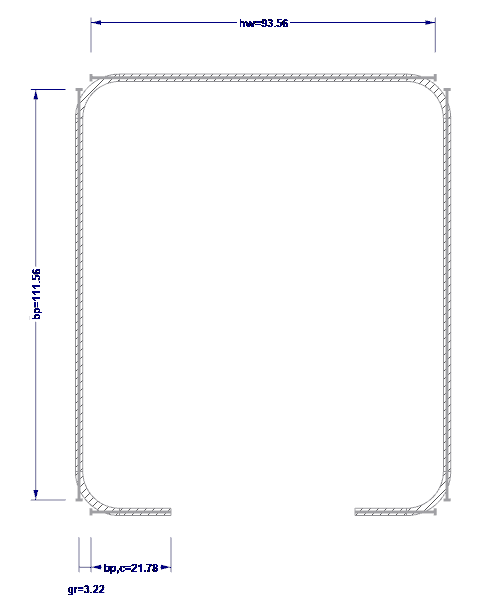
External Dimensions

The external dimensions of the cross-section are shown in Image 02.

2 External Dimensions of Cross-Section in mm

H = 102 mm (web height)
b = 120 mm (belt width)
c = 26 mm (lip length)
t = 2 mm (steel core thickness)

Notional Flat Widths

The notional flat widths are determined according to [1], 5.1. The notional flat widths are shown in Image 03.

3 Notional Flat Widths in mm

r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm

g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3.22 mm

h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3.22 = 93.56 mm

b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3.22 = 111.56 mm

b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3.22 = 21.78 mm

Notional Flat Widths

Checking Width-Thickness Ratios

The width-thickness ratios are checked according to [1], 5.2(1).

b/t = 120/2 = 60 ≤ 60
c/t = 26/2 = 13 ≤ 50
H/t = 102/2 = 51 ≤ 500

The width-thickness ratios are met.

Checking Stiffener Dimensions

The stiffener dimensions are checked according to [1], 5.2(2).
0.2 ≤ c/b = 26/120 = 0.22 ≤ 0.6

The lips can be applied as stiffeners.

Checking Angle Between Stiffener and Planar Element

The angle between the stiffener and the planar element is 90° within the limits of 45° and 135° mentioned in [1], 5.5.3.2(1).

Determining Effective Cross-Section

For steel sections that are not subjected to double symmetry and subjected to compression, the centroidal position of the effective cross-section shifts compared to the gross cross-section. The external compressive force acting centrically on the gross cross-section now acts eccentrically on the effective cross-section, and an additional bending moment is created. According to [1], the additional moments resulting from the shift of the centroid must be taken into account. Subsequently, in addition to the effective cross-section for pure compressive stress, the effective cross-section for pure bending stress must be determined.

Determining Effective Cross-Section Under Pure Compression

According to [2], 4.4(2), the coefficient results in:

ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0.814

Factor ε

Web

According to [2], Table 4.1, the buckling value results in:

k_{σ} = 4

Buckling Value

According to [2], 4.4(2), the buckling slenderness results in:

{\bar{λ}}_{p} = \frac{h_{w} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.012

{\bar{λ}}_{p} = 1.012 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Buckling Slenderness of Web

The slenderness ratio is greater than the limit value 0.673 according to [2], 4.4(2). Thus, a reduction is required.

According to [2], 4.4(2), the reduction factor results in:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.012 - 0.055 \cdot (3 \cdot 1)}{1 . 012^{2}} = 0.773 \leq 1

Reduction Factor for Web

According to [2], Table 4.1, the effective web height results from [2], Table 4.1 in:

h_{eff} = ρ \cdot h_{w} = 0.773 \cdot 93.56 = 72.3 mm

h_{e 1} = h_{e 2} = 0.5 \cdot h_{eff} = 0.5 \cdot 72.3 = 36.17 mm

Effective Height of Web

Flange with Edge Stiffener

In the first step, the first approach for the effective cross-section of the stiffener is determined with the assumption that the edge stiffener acts as a rigid support and that σ_com,Ed = f_yb / γ_M0.

Flange

According to [2], Table 4.1, the buckling value results in:

k_{σ} = 4

Buckling Value

According to [2], 4.4(2), the buckling slenderness results in:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{4}} = 1.207

{\bar{λ}}_{p} = 1.207 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot 1} = 0.673

Buckling Slenderness of Flange

The slenderness ratio is greater than the limit value 0.673 according to [2], 4.4(2). Thus, a reduction is required.

According to [2], 4.4(2), the reduction factor results in:

ρ = \frac{{\bar{λ}}_{p} - 0.055 \cdot (3 \cdot ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1.207 - 0.055 \cdot (3 \cdot 1)}{1 . 207^{2}} = 0.678 \leq 1

Reduction Factor for Flange

According to [2], Table 4.1, the effective flange width results from [2], Table 4.1 in:

b_{eff} = ρ \cdot b_{p} = 0.678 \cdot 111.56 = 75.6 mm

b_{e 1} = b_{e 2} = 0.5 \cdot b_{eff} = 0.5 \cdot 75.6 = 37.79 mm

Effective Flange Width

Edge Stiffener

According to [1], 5.5.3.2(5), the buckling value results in:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

Buckling Value of Edge Stiffener

According to [2], 4.4(2), the buckling slenderness results in:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Buckling Slenderness of Edge Stiffener

The slenderness ratio is smaller than the limit value 0.748 according to [1], 4.4(2). Thus, no reduction is necessary, that is: ρ = 1.0.

According to [1], Eq. 5.13a, the first approach of the effective width results in:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

First Approach of Effective Width

In the second step, the reduction factor for the shape instability of the cross-section is determined using the effective first approach for the cross-section, taking into account the elastic translation spring.

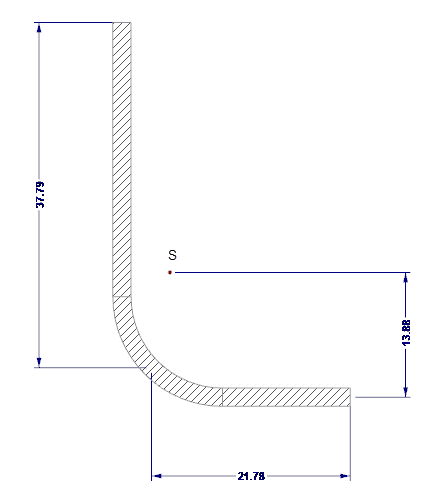
The effective cross-section values of the edge stiffening are calculated with SHAPE-THIN. The edge stiffness is shown in Image 04.

4 Effective Edge Stiffness

A_s = 122.58 mm²
I_s = 7,130 mm⁴
z_s = 13.88 mm

The spring stiffness K of the edge stiffener is determined on the basis of a structural analysis for the entire cross-section. For this purpose, a unit distance load u, acting in the centroid of the effective stiffener, is applied to the cross-section, and the corresponding deformation δ of the stiffener is calculated. For a rectangular cross-section w/h = t/t = 2/2 mm, the deformation results in δ = 3.02 mm (Image 05).

5 Determination of Spring Stiffness

The spring stiffness per unit length K can be calculated according to [1], Eq. 5.9 as follows:

K = \frac{u}{δ} = \frac{1}{3.02 \cdot 2} = 0.166 N / {mm}^{2}

Spring Stiffness per Unit Length

According to [1], Eq. 5.15, the critical stress of the edge stiffener results in:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.166 \cdot 210000 \cdot 7130}}{122.58} = 257 N / {mm}^{2}

Critical Stress of Edge Stiffener

According to [1], Eq. 5.12d, the related slenderness ratio results in:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1.176 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relative Slenderness Ratio

According to [1], 5.5.3.1(7), the reduction factor for the shape instability is calculated as follows:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.176 = 0.62

Reduction Factor for Shape Instability

According to [1], Eq. 5.17, the reduced effective cross-sectional area of the edge stiffener is obtained, taking into account the flexural buckling:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.62 \cdot 122.58 \cdot 1.0 = 76.01 {mm}^{2}

Effective Cross-Sectional Area of Edge Stiffener

Effective Cross-Section Properties Under Pure Compression

The cross-section can be optimized by means of an iterative calculation. For two iterations, it results in the following effective cross-section values:

Area A_eff = 4.62 cm²
Centroidal distance from web z_s,eff = 42.18 mm
Centroidal displacement e_N,y = z_s – z_s,eff = 8.78 mm

Determining Effective Cross-Section Under Pure Bending Stress

Web

The web is subjected to tension and is thus fully effective.

Flange with Edge Stiffener

Flange

According to [2], Table 4.1, the buckling value results in:

ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253.1}{336.2} = - 0.753

k_{σ} = 7.81 - 6.29 \cdot ψ \cdot 9.78 \cdot ψ^{2} = 7.81 - 6.29 \cdot (- 0.753) \cdot 9.78 \cdot {(- 0.753)}^{2} = 18.08

Buckling Value of Flange

According to [2], 4.4(2), the buckling slenderness results in:

{\bar{λ}}_{p} = \frac{b_{p} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111.56 / 2}{28.4 \cdot 0.814 \cdot \sqrt{18.08}} = 0.568

{\bar{λ}}_{p} = 0.568 \geq 0.5 \sqrt{0.085 - 0.055 \cdot ψ} = 0.5 \sqrt{0.085 - 0.055 \cdot (- 0.753)} = 0.856

Buckling Slenderness of Flange

The slenderness ratio is smaller than the limit value 0.856 according to [1], 4.4(2). Thus, no reduction is required.

According to [2], Table 4.1, the effective widths result in:

b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1.0 \cdot 111.56 / (1 \cdot 0.753) = 63.65 mm

b_{e 1} = 0.4 \cdot b_{eff} = 0.4 \cdot 63.65 = 25.46 mm

b_{e 2} = 0.6 \cdot b_{eff} = 0.6 \cdot 63.65 = 38.19 mm

Effective Widths of Flange

Edge Stiffener

According to [1], 5.5.3.2(5), the buckling value results in:

\frac{b_{p, c}}{b_{p}} = \frac{21.78}{111.56} = 0.195 \leq 0.35

k_{σ} = 0.5

Buckling Value of Edge Stiffener

According to [2], 4.4(2), the buckling slenderness results in:

{\bar{λ}}_{p} = \frac{b_{p, c} / t}{28.4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21.78 / 2}{28.4 \cdot 0.814 \cdot \sqrt{0.5}} = 0.666

{\bar{λ}}_{p} = 0.666 \leq 0.748

Buckling Slenderness of Edge Stiffener

The slenderness ratio is smaller than the limit value 0.748 according to [1], 4.4(2). Thus, no reduction is necessary, that is: ρ = 1.0.

According to [1], Eq. 5.13a, the first approach of the effective width results in:

c_{eff} = ρ \cdot b_{p, c} = 1.0 \cdot 21.78 = 21.78 mm

First Approach of Effective Width

The effective cross-section values of the edge stiffening are calculated with SHAPE-THIN. The edge stiffener is shown in Image 06.

6 Effective Stiffening of Cross-Section

A_s = 97.92 mm²
I_s = 6,271 mm⁴
z_s = 8.59 mm

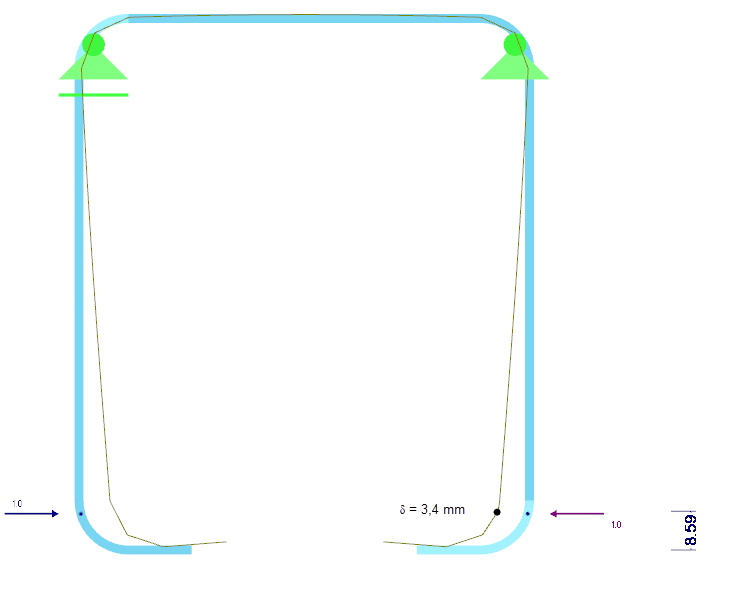
The spring stiffness K of the edge stiffness is determined on the basis of a structural analysis for the entire cross-section. For this purpose, a unit distance load u, acting in the centroid of the effective stiffener, is applied to the cross-section, and the corresponding deformation δ of the stiffener is calculated. For a rectangular cross-section w/h = t/t = 2/2 mm, the deformation results in δ = 3.4 mm (Image 07).

7 Determination of Spring Stiffness

The spring stiffness per unit length K can be calculated according to [1], Eq. 5.9 as follows:

K = \frac{u}{δ} = \frac{1}{3.4 \cdot 2} = 0.146 N / {mm}^{2}

Spring Stiffness per Unit Length

According to [1], Eq. 5.15, the critical stress of the edge stiffener results in:

σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0.146 \cdot 210000 \cdot 6.271}}{97.92} = 283 N / {mm}^{2}

Critical Stress of Edge Stiffener

According to [1], Eq. 5.12d, the related slenderness ratio results in:

{\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1.120 \{\begin{cases} > 0.65 \\ < 1.38 \end{cases}

Relative Slenderness Ratio

According to [1], 5.5.3.1(7), the reduction factor for the shape instability is calculated as follows:

χ_{d} = 1.47 - 0.723 \cdot {\bar{λ}}_{d} = 1.47 - 0.723 \cdot 1.120 = 0.66

Reduction Coefficient for Shape Instability

According to [1], Eq. 5.17, the reduced effective cross-sectional area of the edge stiffener is obtained, taking into account the flexural buckling:

A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0.66 \cdot 97.92 \cdot \frac{355 / 1.0}{312.2} = 73.82 {mm}^{2}

Effective Cross-Sectional Area of Edge Stiffener

Effective Cross-Section Properties Under Pure Bending Stress

All the cross-section parts are fully effective, so iteration is not necessary.

Area A_eff = 6.86 cm²
Section modulus W_{eff, y} = 17.01 cm³

Cross-Section Design of Combined Loading Due to Compression and Bending

The resistance to pure compression is calculated according to [1], 6.1.3(1) as follows:

N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4.62 \cdot \frac{35.5}{1} = 164.16 kN

Resistance to Pure Compression

The resistance to pure bending is calculated according to [1], 6.1.4.1(1) as follows:

M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17.01 \cdot \frac{35.5}{1} = 6.04 kNm

Resistance to Pure Bending

The additional moment resulting from the shift of the centroid is determined according to [1], 6.1.9(2) as follows:

∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8.78 \cdot 10^{- 3} = 1.14 kNm

Additional Moment from Shift of Centroid

According to [1], 6.1.9(1), the design for combined loading from compression and bending results in:

\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164.16} \frac{1.14}{6.04} = 0.98 \leq 1

Design for Combined Loading from Compression and Bending

The design is thus performed.

Modeling Cold-Formed C-Section in SHAPE-THIN

General cold-formed sections can be modeled in SHAPE-THIN. In the general data, activate the "c/t parts and effective cross-section properties" check box (Image 08).

8 General Data

Then, select the "EN 1993-1-3 (Cold-formed cross-section)" option in the "c/t-parts and effective cross-section" tab (Image 09) of the Calculation Parameters dialog box.

The effective cross-section must be determined separately for pure compression and pure bending. Therefore, select the "Neglect additional bending moments due to the shift of the centroid of the effective cross-section" check box.

We have calculated with two iterations in the example, so two iterations are also set in SHAPE-THIN.

The geometric conditions mentioned in [2], 5.2 for the applicability of the standard can be optionally checked. To do this, select the corresponding check boxes.

9 Calculation Parameters

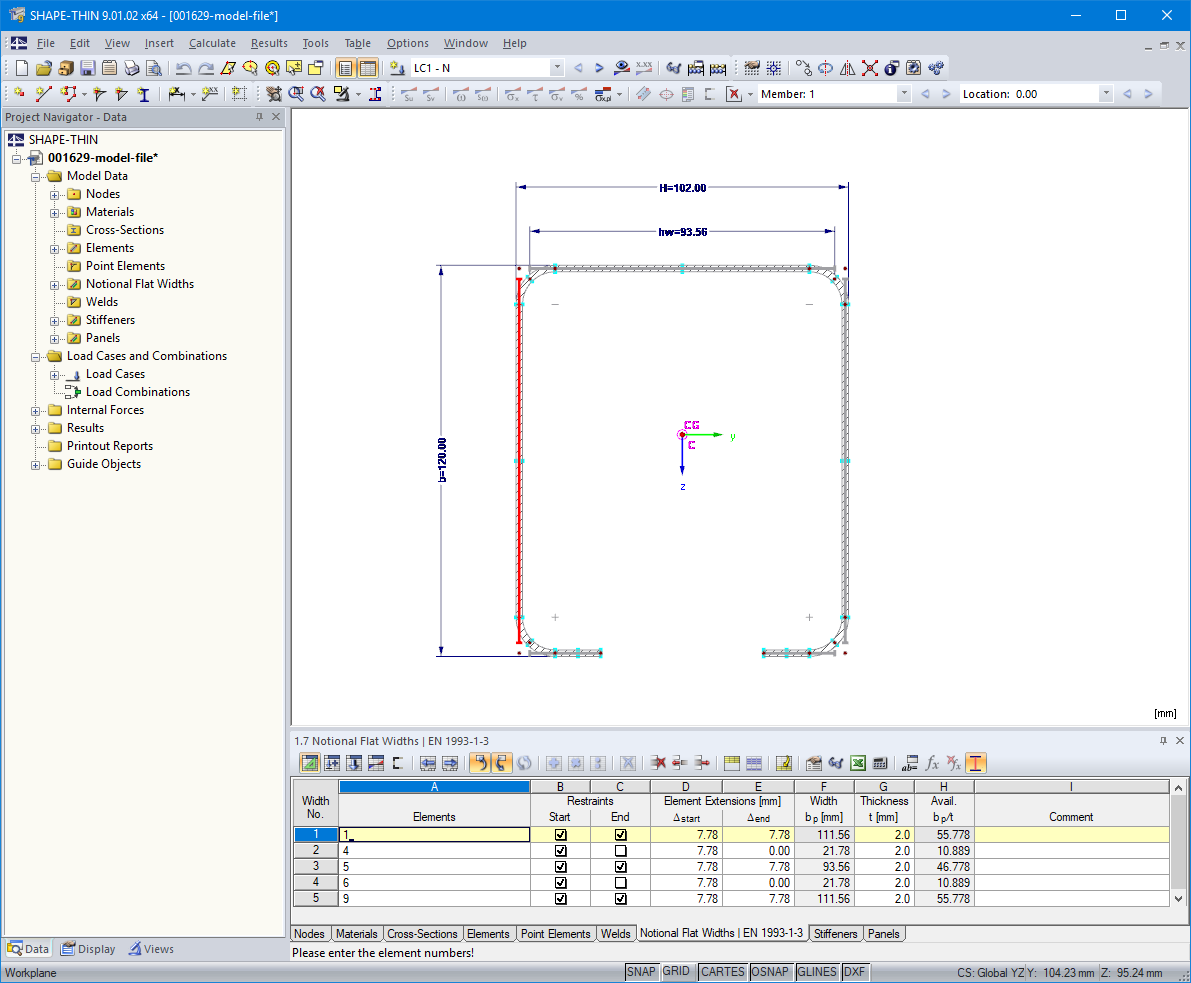
The elements of the cross-section have to be entered first. The notional flat widths are usually generated automatically from the geometry conditions, but can also be created as user-defined in Table "1.7 Notional Flat Widths According to EN 1993-1-3" (Image 10) or in the corresponding dialog box.

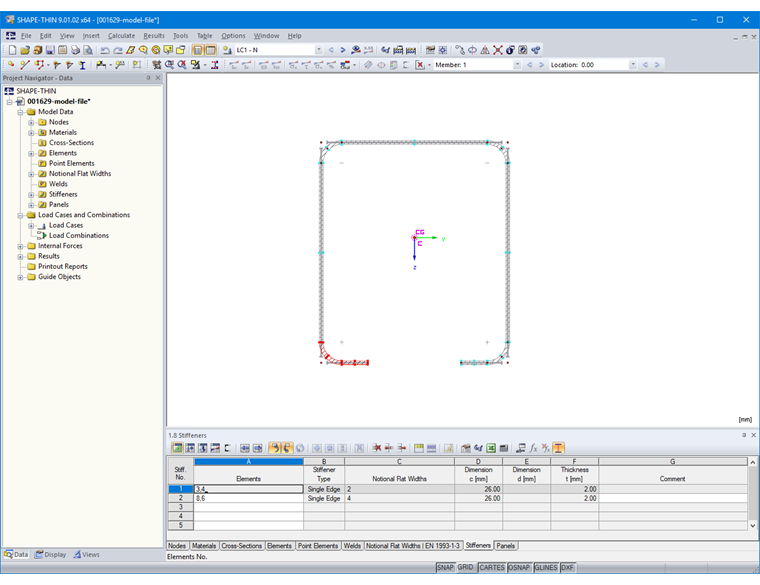
10 Table 1.8 Stiffeners

The stiffeners can then be defined in Table "1.8 Stiffeners" or in the corresponding dialog box (Image 11).

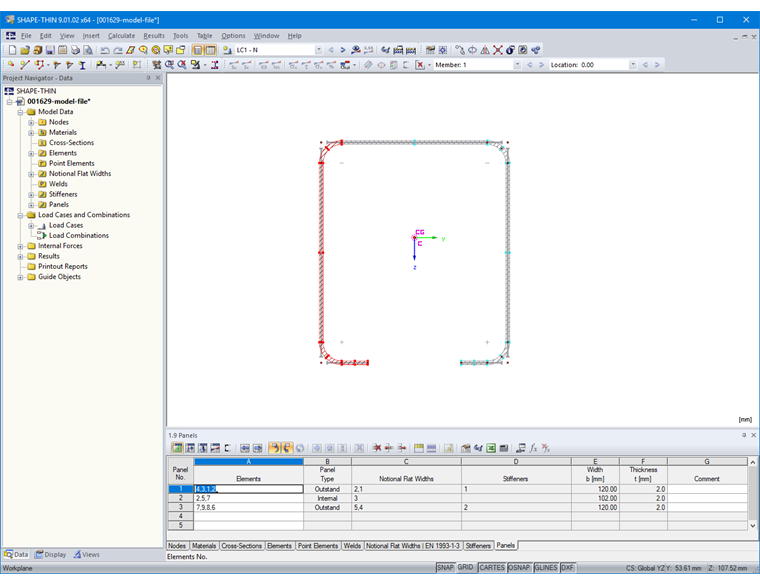
11 Table 1.9 Panels

Furthermore, the buckling panel must be specified in Table "1.9 Panels" (Image 12) or in the corresponding dialog box. To do this, select the elements of the buckling panel. The stiffeners located in the stiffened panel are identified automatically.

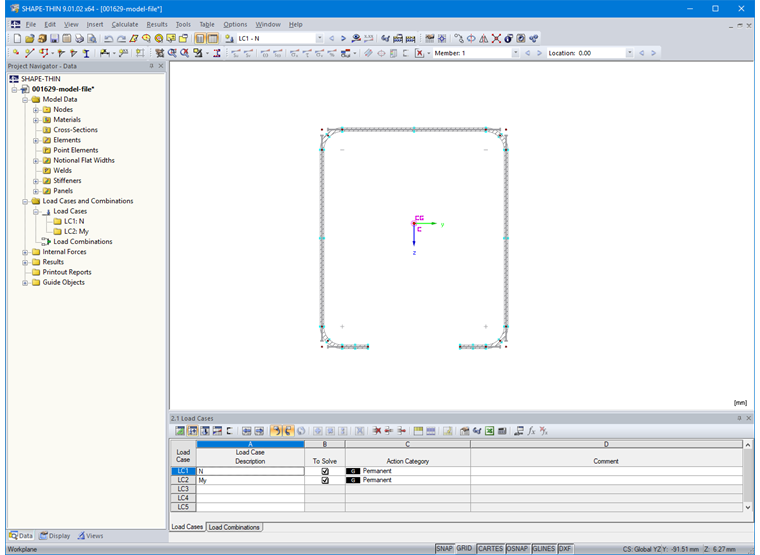
12 Table 2.1 Load Cases

Additionally, a load case for compression force and bending is created in Table "2.1 Load Cases" (Image 13).

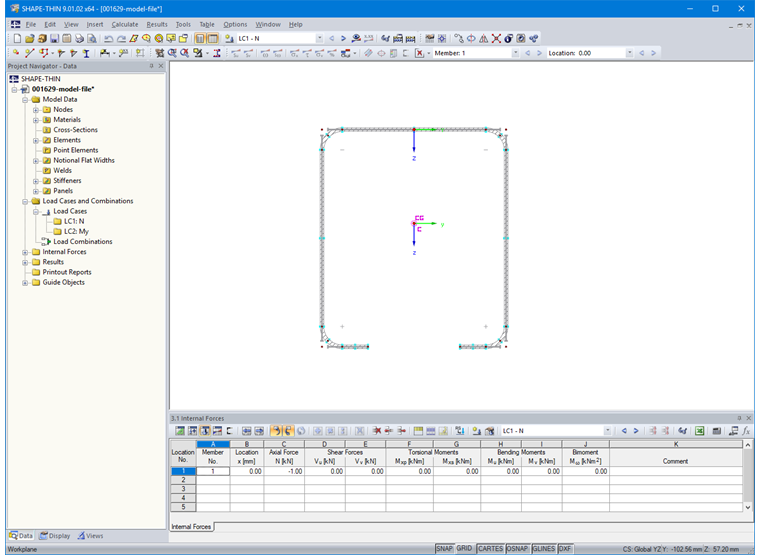
13 Table 3.1 Internal Forces

Then, enter the internal forces in Table "3.1 Internal Forces" or in the corresponding dialog box (Image 14).

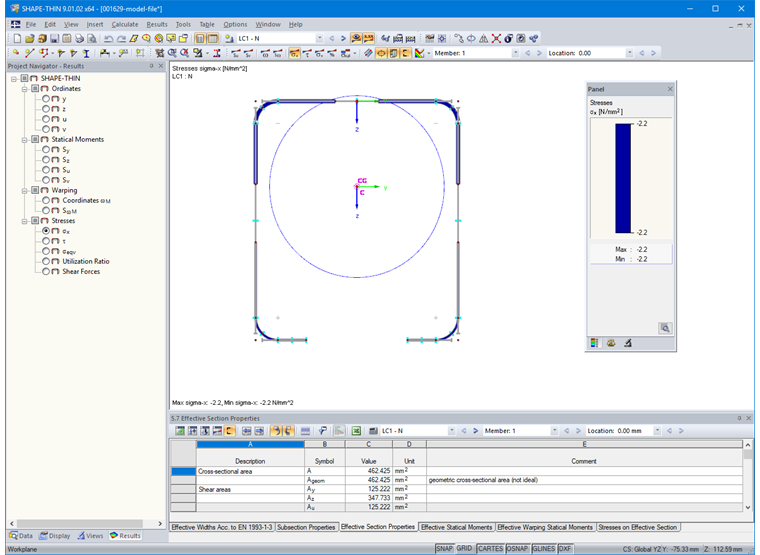
14 Effective Cross-Section Properties

The results of the effective cross-section are available with the "Effective Parts" button (Image 15).

15 General Data

Cross-Section Design of Cold-Formed C-Section in RF-/STEEL Cold-Formed Sections

Cold-formed sections can be designed according to [1] and [2] with the RF-/STEEL Cold-Formed Sections module extension.

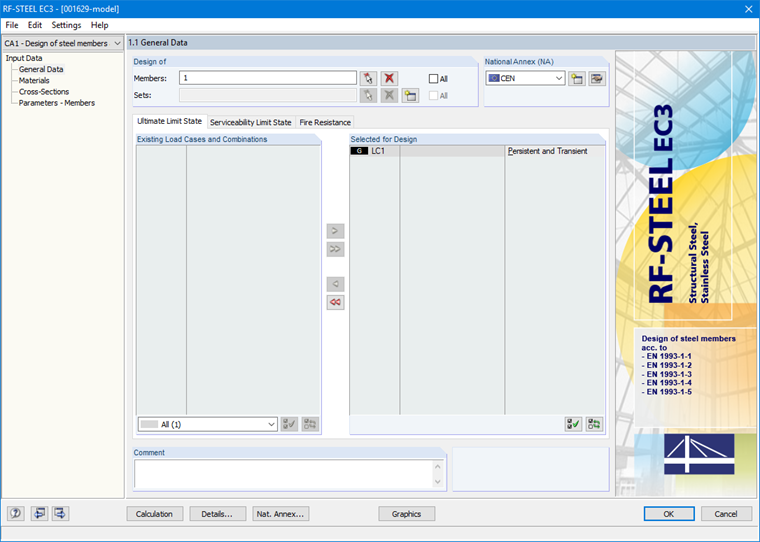
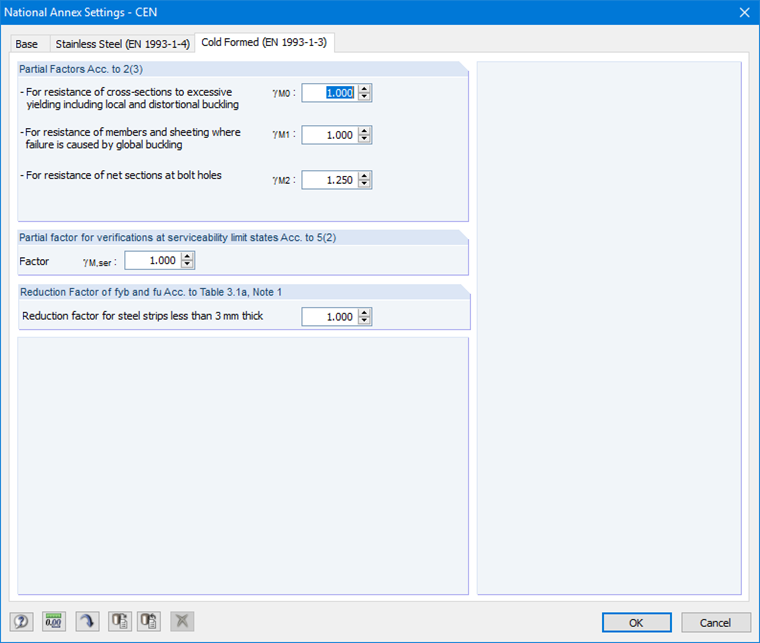
In the General Data, you must first select the member and load case to be designed. "CEN" is selected as the National Annex (Image 16).

16 Parameters of National Annex

You can see and, if necessary, adjust the parameters of the National Annex in the "Cold-Formed (EN 1993-1-3)" tab of the corresponding window (Image 17).

17 Details, Cold-Formed Sections Tab

In the Detail settings, activate the design check for cold-formed sections in the "Cold-Formed" tab (Image 18).

18 Details, Stability Tab

Only the cross-section design should be performed. Therefore, the "Perform stability analysis" check box in the "Stability" tab of the detail settings must be deactivated (Image 19).

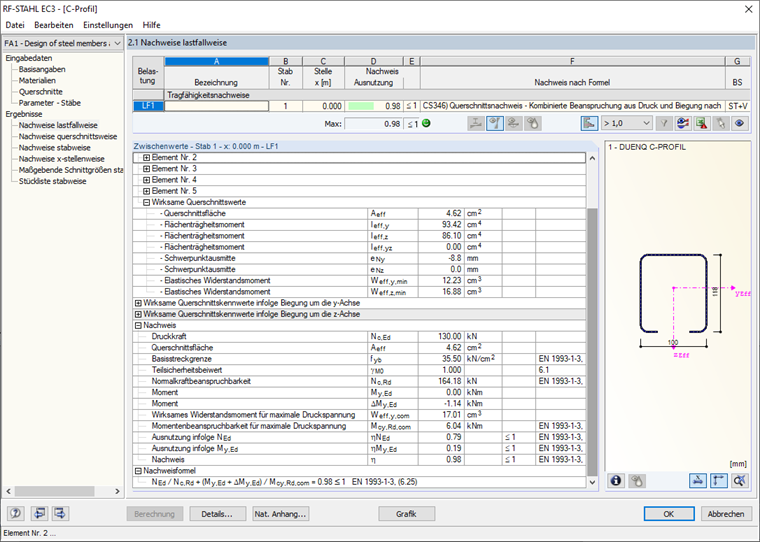
19 Figure 20 - Results

After the calculation, the corresponding output tables show, among other things, effective cross-section properties due to axial force N, bending moment M_y, bending moment M_z, internal forces, and the entire design (Image 20).

20 Table 1.7 Notional Flat Widths | EN 1993-1-3

Knowledge Base

KB 001629 | Design of Thin-Walled, Cold-Formed C-Section According to EN 1993-1-3

Author

Ms. von Bloh provides technical support for our customers and is responsible for the development of the SHAPE‑THIN program as well as steel and aluminum structures.

Links

References

European Committee for Standardization. (2010). Eurocode 3: Design of Steel Structures – Part 1‑3: General Rules – Supplementary Rules for Cold-Formed Members and Sheeting, EN 1993‑1‑3:2010‑12. Berlin: Beuth.
European Committee for Standardization (CEN). (2009). Eurocode 3: Design of Steel Structures – Part 1-5: General Rules – Plated Structural Elements, EN 1993-1-5:2006 + AC:2009. Beuth Verlag GmbH, Berlin.
Kuhlmann, U. (2009). Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlin: Ernst & Sohn.

Downloads

Model of Technical Article | SHAPE-THIN 9 File

912 KB

Model of Technical Article | RFEM 5 File

504 KB

Model of Technical Article | RSTAB-8 File

404 KB

;