Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

Fachbeitrag

Zurück zu Knowledge Base

KB 001629 | Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

01
System und Belastung (Abmessungen in mm, Kraft in kN)

02
Außenabmessungen des Querschnitts in mm

03
Nennwerte der geraden Breiten in mm

04
Wirksame Randsteife

05
Ermittlung der Federsteifigkeit

06
Wirksamer Steifenquerschnitt

07
Ermittlung der Federsteifigkeit

08
Basisangaben

09
Berechnungsparameter

Zurück zu Knowledge Base

2. März 2020

001629

Statische Berechnungen

Spannungsberechnungen

Eurocode 3

Der Tragfähigkeitsnachweis für kaltgeformte Profile nach EN 1993-1-3 und EN 1993-1-5 kann mit der Modulerweiterung RF-/STAHL Kaltgeformte Profile geführt werden. Neben den kaltgeformten Profilen aus der Querschnittsdatenbank können auch allgemeine Profile aus DUENQ nachgewiesen werden.

Im folgenden Beispiel aus dem Stahlbau-Kalender 2009 [3] wird der Querschnittsnachweis für einen Einfeldträger mit dünnwandigem, kaltgeformtem C-Profil unter Normalkraftbeanspruchung geführt. Das C-Profil wird in DUENQ modelliert und dann in RF-/STAHL Kaltgeformte Profile nachgewiesen.

System

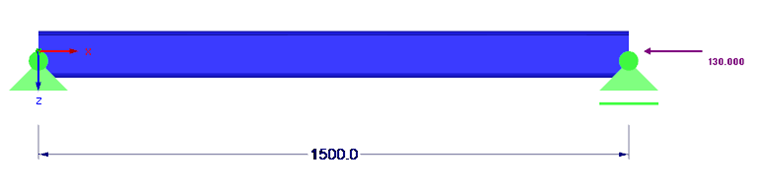
System und Beanspruchung sind in Bild 01 dargestellt.

Bild 01 - System und Belastung (Abmessungen in mm, Kraft in kN)

Material

S 355 EN 10025-2
E = 210.000 N/mm²
G = 80.769 N/mm²
ν = 0,3
f_y = f_yb = 355 N/mm²
γ_M0 = γ_M1 = 1,00 (Nachweis nach CEN)

Außenabmessungen

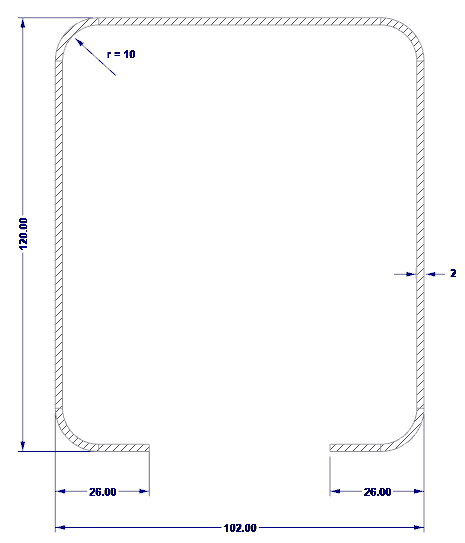
Die Außenabmessungen des Querschnitts sind in Bild 02 dargestellt.

Bild 02 - Außenabmessungen des Querschnitts in mm

H = 102 mm (Steghöhe)
b = 120 mm (Gurtbreite)
c = 26 mm (Lippenlänge)
t = 2 mm (Stahlkerndicke)

Nennwerte der geraden Breiten

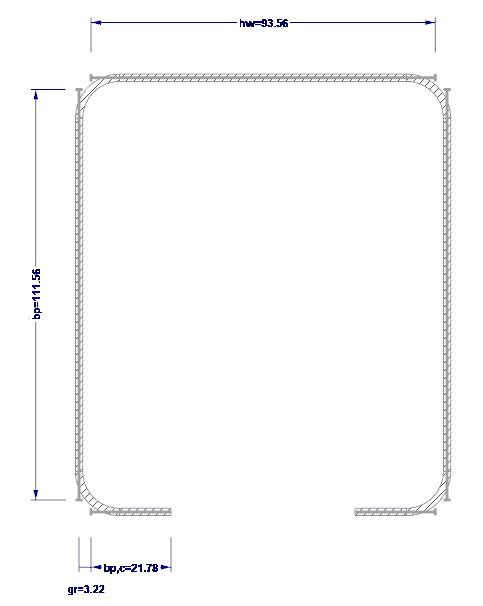
Die Nennwerte der geraden Breiten werden gemäß [1], 5.1 ermittelt. Die Nennwerte der geraden Breiten sind in Bild 03 dargestellt.

Bild 03 - Nennwerte der geraden Breiten in mm

Formel 1

$r_{m} = r \frac{t}{2} = 10 \frac{2}{2} = 11 mm g_{r} = r_{m} \cdot (\tan (\frac{ϕ}{2}) - \sin (\frac{ϕ}{2})) = 11 \cdot (\tan 45 ° - \sin 45 °) = 3, 22 mm h_{w} = H - t - 2 \cdot g_{r} = 102 - 2 - 2 \cdot 3, 22 = 93, 56 mm b_{p} = b - t - 2 \cdot g_{r} = 120 - 2 - 2 \cdot 3, 22 = 111, 56 mm b_{p, c} = c - \frac{t}{2} - g_{r} = 26 - \frac{2}{2} - 3, 22 = 21, 78 mm$

Überprüfung der Breiten-Dicken-Verhältnisse

Die Breiten-Dicken-Verhältnisse werden gemäß [1], 5.2(1) überprüft.

b / t = 120 / 2 = 60 ≤ 60

c / t = 26 / 2 = 13 ≤ 50

H / t = 102 / 2 = 51 ≤ 500

Die Breiten-Dicken-Verhältnisse sind eingehalten.

Überprüfung der Steifenabmessungen

Die Steifenabmessungen werden gemäß [1], 5.2(2) überprüft.

0,2 ≤ c / b = 26 / 120 = 0,22 ≤ 0,6

Die Lippen können als Steifen angesetzt werden.

Überprüfung des Winkels zwischen Steife und ebenem Element

Der Winkel zwischen Steife und ebenem Element liegt mit 90 ° innerhalb der in [1], 5.5.3.2(1) genannten Grenzen von 45 ° und 135 °.

Ermittlung des wirksamen Querschnitts

Bei nicht doppeltsymmetrischen, druckbeanspruchten, lokal beulgefährdeten Stahlprofilen verschiebt sich die Schwerpunktlage des wirksamen Querschnitts im Vergleich zum Bruttoquerschnitt. Die zentrisch am Bruttoquerschnitt angreifende äußere Druckkraft wirkt am wirksamen Querschnitt nun außermittig und es entsteht ein zusätzliches Biegemoment. Nach [1] sind die sich aus der Schwerachsenverschiebung ergebenden Zusatzmomente zu berücksichtigen. In der Folge ist neben dem wirksamen Querschnitt für reine Druckbeanspruchung auch der wirksame Querschnitt für reine Biegebeanspruchung zu ermitteln.

Ermittlung des wirksamen Querschnitts unter reiner Druckbeanspruchung

Der Beiwert ergibt sich nach [2], 4.4(2) zu:

Formel 2

$ε = \sqrt{\frac{235}{f_{yb}}} = \sqrt{\frac{235}{355}} = 0, 814$

Steg:

Der Beulwert ergibt sich nach [2], Tab. 4.1 zu:

Formel 3

$k_{σ} = 4$

Die Beulschlankheit ergibt sich nach [2], 4.4(2) zu:

Formel 4

${\bar{λ}}_{p} = \frac{h_{w} / t}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{93, 56 / 2}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 1, 012 {\bar{λ}}_{p} = 1, 012 \geq 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ} = 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$

Der Schlankheitsgrad ist größer als der Grenzwert 0,673 nach [2], 4.4(2). Es ist somit eine Abminderung erforderlich.

Der Abminderungsfaktor ergibt sich nach [2], 4.4(2) zu:

Formel 5

$ρ = \frac{{\bar{λ}}_{p} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1, 012 - 0, 055 \cdot (3 1)}{1, 012^{2}} = 0, 773 \leq 1$

Die wirksame Steghöhe ergibt sich nach [2], Tab. 4.1 zu:

Formel 6

$h_{eff} = ρ \cdot h_{w} = 0, 773 \cdot 93, 56 = 72, 3 mm h_{e 1} = h_{e 2} = 0, 5 \cdot h_{eff} = 0, 5 \cdot 72, 3 = 36, 17 mm$

Gurte mit Randsteife:

Im ersten Schritt wird ein erster Ansatz für den wirksamen Querschnitt der Steife mit der Annahme ermittelt, dass die Randsteife als festes Auflager wirkt und dass σ_com,Ed = f_yb / γ_M0 ist.

Gurt:

Der Beulwert ergibt sich nach [2], Tab. 4.1 zu:

Formel 3

$k_{σ} = 4$

Die Beulschlankheit ergibt sich nach [2], 4.4(2) zu:

Formel 7

${\bar{λ}}_{p} = \frac{b_{p} / t}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111, 56 / 2}{28, 4 \cdot 0, 814 \cdot \sqrt{4}} = 1, 207 {\bar{λ}}_{p} = 1, 207 \geq 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ} = 0, 5 \sqrt{0, 085 - 0, 055 \cdot 1} = 0, 673$

Der Schlankheitsgrad ist größer als der Grenzwert 0,673 nach [2], 4.4(2). Es ist somit eine Abminderung erforderlich.

Der Abminderungsfaktor ergibt sich nach [2], 4.4(2) zu:

Formel 8

$ρ = \frac{{\bar{λ}}_{p} - 0, 055 \cdot (3 ψ)}{{\bar{λ}}_{p}^{2}} = \frac{1, 207 - 0, 055 \cdot (3 1)}{1, 207^{2}} = 0, 678 \leq 1$

Die wirksame Gurtbreite ergibt sich nach [2], Tab. 4.1 zu:

Formel 9

$b_{eff} = ρ \cdot b_{p} = 0, 678 \cdot 111, 56 = 75, 6 mm b_{e 1} = b_{e 2} = 0, 5 \cdot b_{eff} = 0, 5 \cdot 75, 6 = 37, 79 mm$

Randsteife:

Der Beulwert ergibt sich nach [1], 5.5.3.2(5) a zu:

Formel 10

$\frac{b_{p, c}}{b_{p}} = \frac{21, 78}{111, 56} = 0, 195 \leq 0, 35 k_{σ} = 0, 5$

Die Beulschlankheit ergibt sich nach [2], 4.4(2) zu:

Formel 11

${\bar{λ}}_{p} = \frac{b_{p, c} / t}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21, 78 / 2}{28, 4 \cdot 0, 814 \cdot \sqrt{0, 5}} = 0, 666 {\bar{λ}}_{p} = 0, 666 \leq 0, 748$

Der Schlankheitsgrad ist kleiner als der Grenzwert 0,748 nach [1], 4.4(2). Es ist somit keine Abminderung notwendig, das heißt: ρ = 1,0.

Der erste Ansatz der wirksamen Breite ergibt sich nach [1], Gl. 5.13a zu:

Formel 12

$c_{eff} = ρ \cdot b_{p, c} = 1, 0 \cdot 21, 78 = 21, 78 mm$

Im zweiten Schritt wird der Abminderungsfaktor für die Forminstabilität des Querschnitts unter Verwendung des wirksamen ersten Ansatzes für den Querschnitt unter Berücksichtigung der elastischen kontinuierlichen Verschiebungsfeder bestimmt.

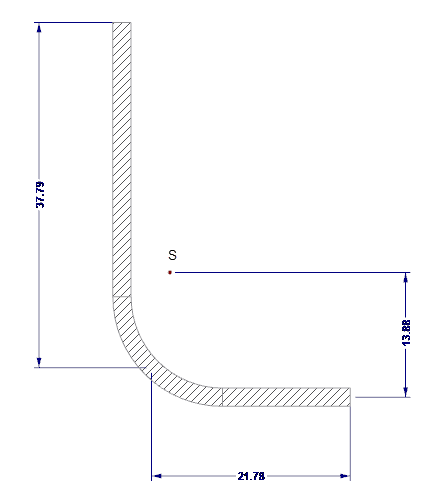
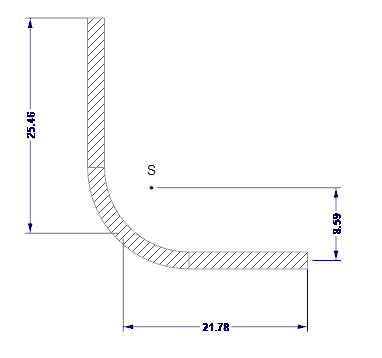
Die wirksamen Querschnittswerte der Randsteife werden mit DUENQ berechnet. Die Randsteife ist in Bild 04 dargestellt.

Bild 04 - Wirksame Randsteife

A_s = 122,58 mm²
I_s = 7.130 mm⁴
z_s = 13,88 mm

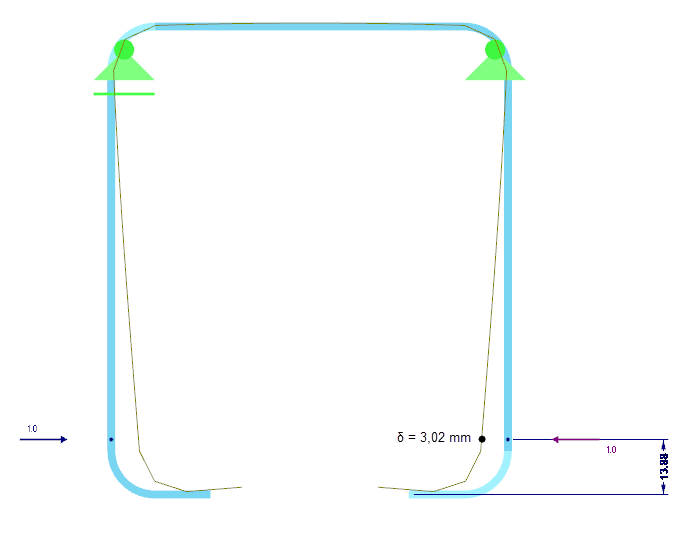
Die Federsteifigkeit K der Randsteife wird auf Basis einer statischen Analyse für den Gesamtquerschnitt bestimmt. Dazu wird eine Einheitsstreckenlast u, im Schwerpunkt der wirksamen Steife angreifend, am Profil angesetzt und die zugehörige Verformung δ der Steife berechnet. Für einen Rechteckquerschnitt b / h = t / t = 2 / 2 mm ergibt sich die Verformung zu δ = 3,02 mm (Bild 05).

Bild 05 - Ermittlung der Federsteifigkeit

Die Federsteifigkeit je Längeneinheit K kann gemäß [1], Gl. 5.9 berechnet werden mit:

Formel 13

$K = \frac{u}{δ} = \frac{1}{3, 02 \cdot 2} = 0, 166 N / {mm}^{2}$

Die kritische Verzweigungsspannung der Randsteife ergibt sich nach [1], Gl. 5.15 zu:

Formel 14

$σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0, 166 \cdot 210.000 \cdot 7.130}}{122, 58} = 257 N / {mm}^{2}$

Der bezogene Schlankheitsgrad ergibt sich gemäß [1], Gl. 5.12d zu:

Formel 15

${\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{257}} = 1, 176 \{\begin{cases} > 0, 65 \\ < 1, 38 \end{cases}$

Der Abminderungsbeiwert für die Forminstabilität ergibt sich gemäß [1], 5.5.3.1(7) zu:

Formel 16

$χ_{d} = 1, 47 - 0, 723 \cdot {\bar{λ}}_{d} = 1, 47 - 0, 723 \cdot 1, 176 = 0, 62$

Die reduzierte, wirksame Querschnittsfläche der Randsteife ergibt sich unter Berücksichtigung des Biegeknickens gemäß [1], Gl. 5.17 zu:

Formel 17

$A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0, 62 \cdot 122, 58 \cdot 1, 0 = 76, 01 {mm}^{2}$

Wirksame Querschnittswerte unter reiner Druckbeanspruchung:

Der Querschnitt kann mithilfe einer iterativen Berechnung optimiert werden. Für zwei Iterationen ergeben sich folgende wirksame Querschnittswerte:

Fläche A_eff = 4,62 cm²
Schwerpunktabstand vom Steg z_s,eff = 42,18 mm
Schwerpunktverschiebung e_N,y = z_s – z_s,eff = 50,96 - 42,18 = 8,78 mm

Ermittlung des wirksamen Querschnitts unter reiner Biegebeanspruchung

Steg:

Der Steg ist zugbeansprucht und damit voll wirksam.

Gurte mit Randsteife:

Im ersten Schritt wird ein erster Ansatz für den wirksamen Querschnitt der Steife mit der Annahme ermittelt, dass die Randsteife als festes Auflager wirkt und dass σ_com,Ed = f_yb / γ_M0 ist.

Gurt:

Der Beulwert ergibt sich nach [2], Tab. 4.1 zu:

Formel 18

$ψ = \frac{σ_{2}}{σ_{1}} = \frac{- 253, 1}{336, 2} = - 0, 753 k_{σ} = 7, 81 - 6, 29 \cdot ψ 9, 78 \cdot ψ^{2} = 7, 81 - 6, 29 \cdot (- 0, 753) 9, 78 \cdot {(- 0, 753)}^{2} = 18, 08$

Die Beulschlankheit ergibt sich nach [2], 4.4(2) zu:

Formel 19

${\bar{λ}}_{p} = \frac{b_{p} / t}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{111, 56 / 2}{28, 4 \cdot 0, 814 \cdot \sqrt{18, 08}} = 0, 568 {\bar{λ}}_{p} = 0, 568 \geq 0, 5 \sqrt{0, 085 - 0, 055 \cdot ψ} = 0, 5 \sqrt{0, 085 - 0, 055 \cdot (- 0, 753)} = 0, 856$

Der Schlankheitsgrad ist kleiner als der Grenzwert 0,856 nach [2], 4.4(2). Es ist somit keine Abminderung erforderlich.

Die wirksamen Breiten ergeben sich gemäß [2], Tab. 4.1 zu:

Formel 20

$b_{eff} = ρ \cdot b_{p} / (1 - ψ) = 1, 0 \cdot 111, 56 / (1 0, 753) = 63, 65 mm b_{e 1} = 0, 4 \cdot b_{eff} = 0, 4 \cdot 63, 65 = 25, 46 mm b_{e 2} = 0, 6 \cdot b_{eff} = 0, 6 \cdot 63, 65 = 38, 19 mm$

Randsteife:

Der Beulwert ergibt sich nach [1], 5.5.3.2(5) a zu:

Formel 10

$\frac{b_{p, c}}{b_{p}} = \frac{21, 78}{111, 56} = 0, 195 \leq 0, 35 k_{σ} = 0, 5$

Die Beulschlankheit ergibt sich nach [2], 4.4(2) zu:

Formel 11

${\bar{λ}}_{p} = \frac{b_{p, c} / t}{28, 4 \cdot ε \cdot \sqrt{k_{σ}}} = \frac{21, 78 / 2}{28, 4 \cdot 0, 814 \cdot \sqrt{0, 5}} = 0, 666 {\bar{λ}}_{p} = 0, 666 \leq 0, 748$

Der Schlankheitsgrad ist kleiner als der Grenzwert 0,748 nach [1], 4.4(2). Es ist somit keine Abminderung notwendig, das heißt: ρ = 1,0.

Der erste Ansatz der wirksamen Breite ergibt sich nach [1], Gl. 5.13a zu:

Formel 12

$c_{eff} = ρ \cdot b_{p, c} = 1, 0 \cdot 21, 78 = 21, 78 mm$

Die wirksamen Querschnittswerte der Randsteife werden mit DUENQ berechnet. Die Randsteife ist in Bild 06 dargestellt.

Bild 06 - Wirksamer Steifenquerschnitt

A_s = 97,92 mm²
I_s = 6.271 mm⁴
z_s = 8,59 mm

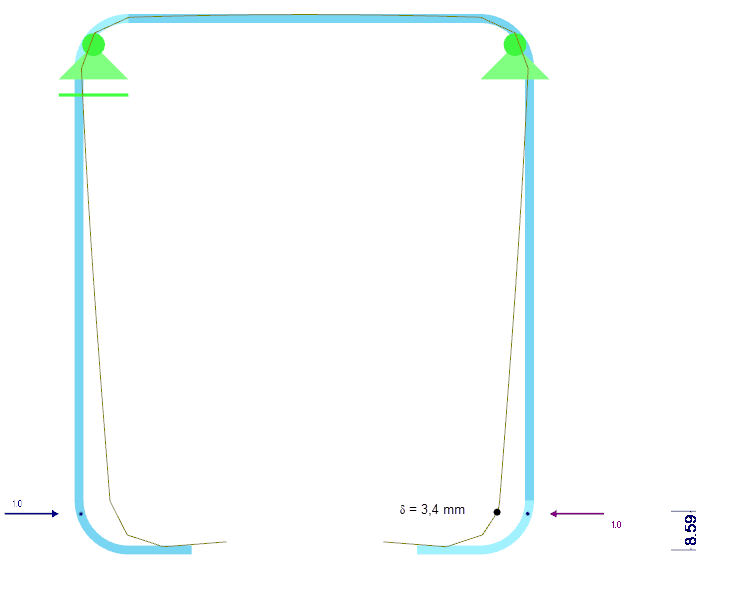
Bild 07 - Ermittlung der Federsteifigkeit

Die Federsteifigkeit je Längeneinheit K kann gemäß [1], Gl. 5.9 berechnet werden mit:

Formel 21

$K = \frac{u}{δ} = \frac{1}{3, 4 \cdot 2} = 0, 146 N / {mm}^{2}$

Die kritische Verzweigungsspannung der Randsteife ergibt sich nach [1], Gl. 5.15 zu:

Formel 22

$σ_{cr, s} = \frac{2 \cdot \sqrt{K \cdot E \cdot I_{s}}}{A_{s}} = \frac{2 \cdot \sqrt{0, 146 \cdot 210.000 \cdot 6.271}}{97, 92} = 283 N / {mm}^{2}$

Der bezogene Schlankheitsgrad ergibt sich gemäß [1], Gl. 5.12d zu:

Formel 23

${\bar{λ}}_{d} = \sqrt{\frac{f_{yb}}{σ_{cr, s}}} = \sqrt{\frac{355}{283}} = 1, 120 \{\begin{cases} > 0, 65 \\ < 1, 38 \end{cases}$

Der Abminderungsbeiwert für die Forminstabilität ergibt sich gemäß [1], 5.5.3.1(7) zu:

Formel 24

$χ_{d} = 1, 47 - 0, 723 \cdot {\bar{λ}}_{d} = 1, 47 - 0, 723 \cdot 1, 120 = 0, 66$

Die reduzierte, wirksame Querschnittsfläche der Randsteife ergibt sich unter Berücksichtigung des Biegeknickens gemäß [1], Gl. 5.17 zu:

Formel 25

$A_{s, red} = χ_{d} \cdot A_{s} \cdot \frac{f_{yb} / γ_{M 0}}{σ_{com, Ed}} = 0, 66 \cdot 97, 92 \cdot \frac{355 / 1, 0}{312, 2} = 73, 82 {mm}^{2}$

Wirksame Querschnittswerte unter reiner Biegebeanspruchung:

Alle Querschnittsteile sind voll wirksam, so dass eine Iteration nicht notwendig ist.

Fläche A_eff = 6,86 cm²
Widerstandsmoment W_eff,y = 17,01 cm³

Querschnittsnachweis kombinierte Beanspruchung aus Druck und Biegung

Die Beanspruchbarkeit für reinen Druck berechnet sich gemäß [1], 6.1.3(1) zu:

Formel 26

$N_{c, Rd} = A_{eff} \cdot \frac{f_{yb}}{γ_{M 0}} = 4, 62 \cdot \frac{35, 5}{1} = 164, 16 kN$

Die Beanspruchbarkeit für reine Biegung berechnet sich gemäß [1], 6.1.4.1(1) zu:

Formel 27

$M_{cy, Rd, com} = W_{eff, y} \cdot \frac{f_{yb}}{γ_{M 0}} = 17, 01 \cdot \frac{35, 5}{1} = 6, 04 kNm$

Das sich aus der Schwerachsenverschiebung ergebende Zusatzmoment wird gemäß [1], 6.1.9(2) bestimmt zu:

Formel 28

$∆ M_{y, Ed} = N_{Ed} \cdot e_{Ny} = 130 \cdot 8, 78 \cdot 10^{- 3} = 1, 14 kNm$

Der Nachweis für kombinierte Beanspruchung aus Druck und Biegung ergibt sich gemäß [1], 6.1.9(1) zu:

Formel 29

$\frac{N_{Ed}}{N_{c, Rd}} \frac{∆ M_{y, Ed}}{M_{cy, Rd, com}} = \frac{130}{164, 16} \frac{1, 14}{6, 04} = 0, 98 \leq 1$

Der Nachweis ist damit erbracht.

Modellierung des kaltgeformten C-Profils in DUENQ

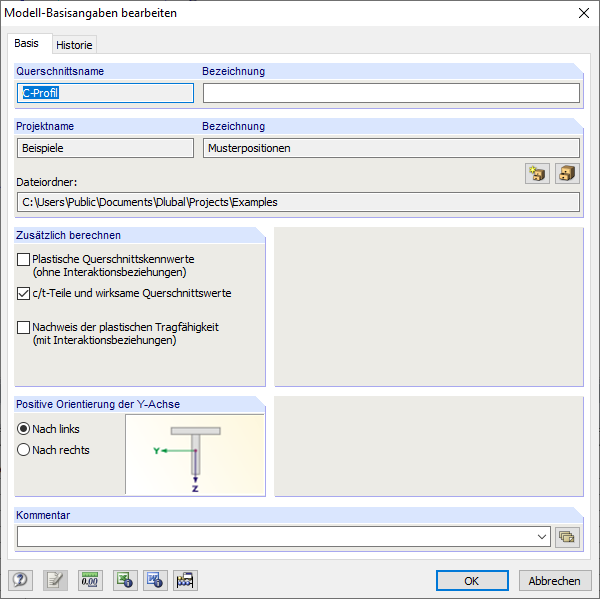
Allgemeine kaltgeformte Profile können in DUENQ modelliert werden. In den Basisangaben ist das Kontrollfeld "c/t-Teile und wirksame Querschnittswerte" zu aktivieren (Bild 08).

Bild 08 - Basisangaben

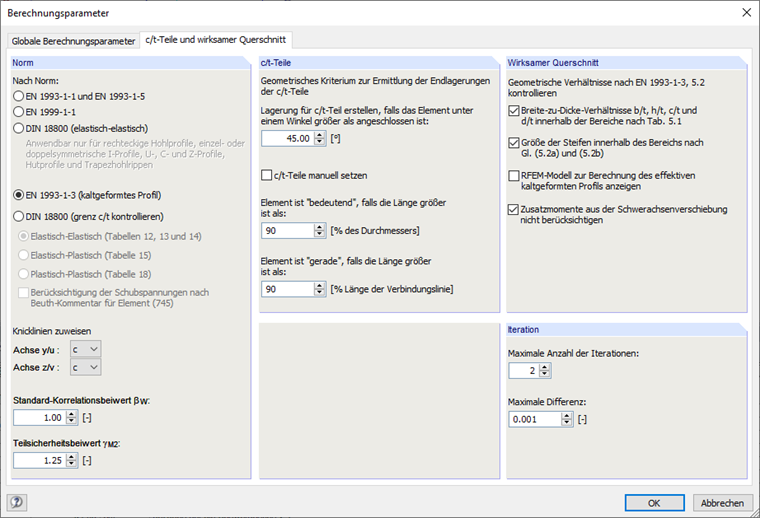
Danach ist im Register "c/t-Teile und wirksamer Querschnitt" (Bild 09) der Berechnungsparameter die Option "EN 1993-1-3 (kaltgeformtes Profil)" auszuwählen.

Der wirksame Querschnitt ist getrennt für reine Druckbeanspruchung und reine Biegebeanspruchung zu ermitteln. Daher ist das Kontrollkästchen "Zusatzmomente aus der Schwerachsenverschiebung nicht berücksichtigen" zu aktivieren.

Im Beispiel wurde mit zwei Iterationen gerechnet, sodass auch in DUENQ zwei Iterationen eingestellt werden.

Die in [2], 5.2 genannten geometrischen Verhältnisse zur Anwendbarkeit der Norm können optional überprüft werden. Hierzu sind die entsprechenden Kontrollkästchen zu aktivieren.

Bild 09 - Berechnungsparameter

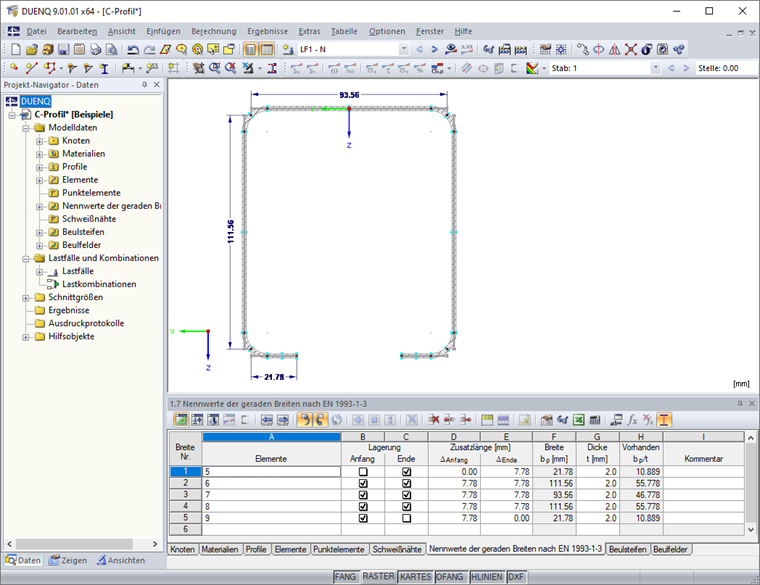
Es sind zunächst die Elemente des Querschnitts einzugeben. Die Nennwerte der geraden Breiten werden in der Regel automatisch aus den Geometriebedingungen erzeugt, können aber auch benutzerdefiniert in Tabelle "1.7 Nennwerte der geraden Breiten nach EN 1993-1-3" (Bild 10) oder dem entsprechenden Dialog angelegt werden.

Bild 10 - Tabelle 1.7 Nennwerte der geraden Breiten nach EN 1993-1-3

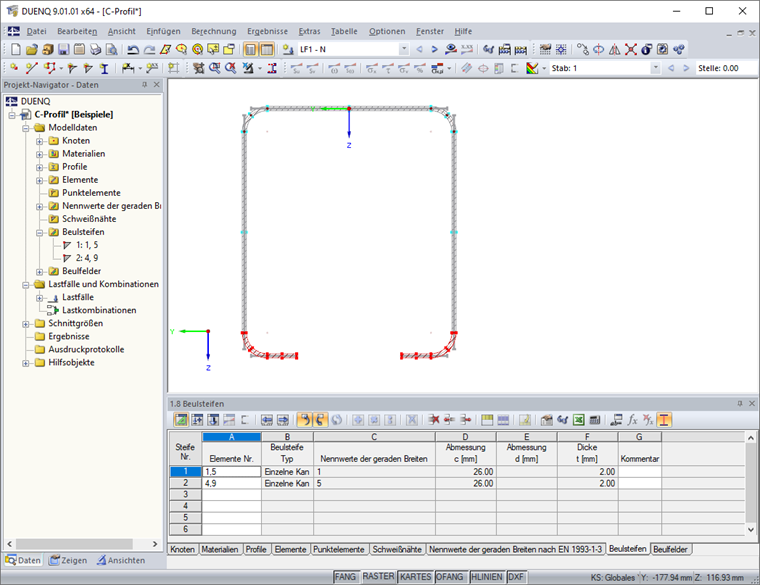
Die Beulsteifen können dann in der Tabelle "1.8 Beulsteifen" beziehungsweise dem entsprechenden Dialog definiert werden (Bild 11).

Bild 11 - Tabelle 1.8 Beulsteifen

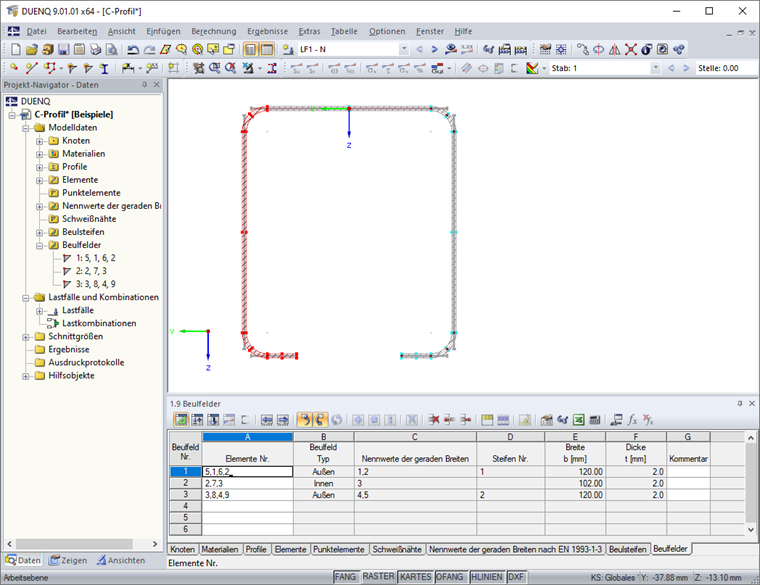
Des Weiteren ist das Beulfeld in Tabelle "1.9 Beulfelder" (Bild 12) beziehungsweise im entsprechenden Dialog anzugeben. Dazu sind die Elemente des Beulfelds auszuwählen. Die im Beulfeld liegenden Steifen werden automatisch erkannt.

Bild 12 - Tabelle 1.9 Beulfelder

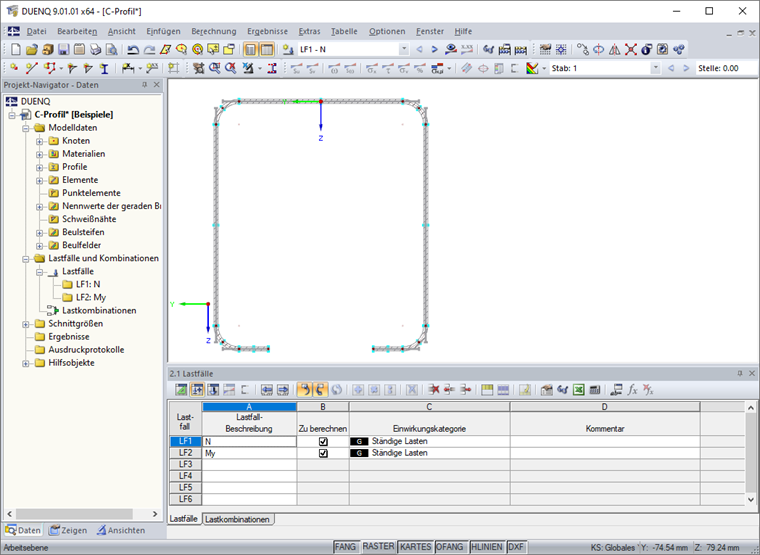
Außerdem wird jeweils ein Lastfall für Druckkraft und Biegung in Tabelle "2.1 Lastfälle" angelegt (Bild 13).

Bild 13 - Tabelle 2.1 Lastfälle

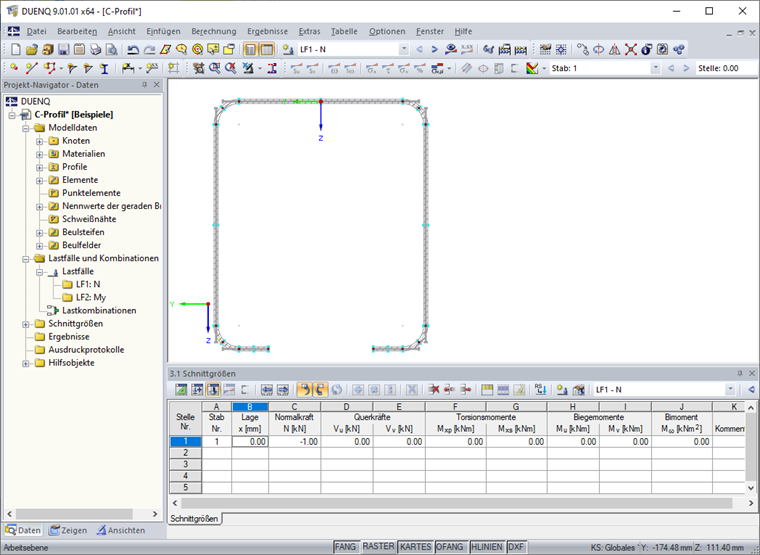
In der Tabelle "3.1 Schnittgrößen" beziehungsweise dem entsprechenden Dialog sind dann die Schnittgrößen einzugeben (Bild 14).

Bild 14 - Tabelle 3.1 Schnittgrößen

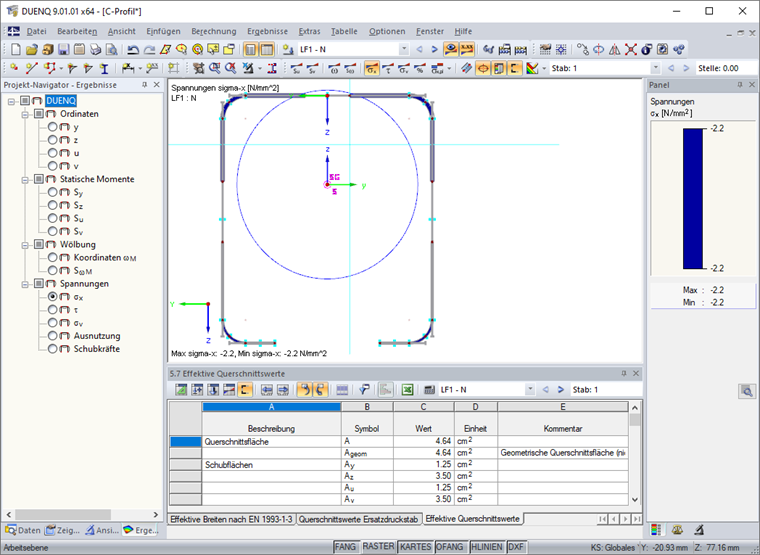
Die Ergebnisse des wirksamen Querschnitts sind mit der Schaltfläche "Wirksame Breiten" zugänglich (Bild 15).

Bild 15 - Wirksame Querschnittswerte

Querschnittsnachweis des kaltgeformten C-Profils in RF-/ STAHL Kaltgeformte Profile

Kaltgeformte Profile können nach [1] und [2] mit der Modulerweiterung RF-/ STAHL Kaltgeformte Profile nachgewiesen werden.

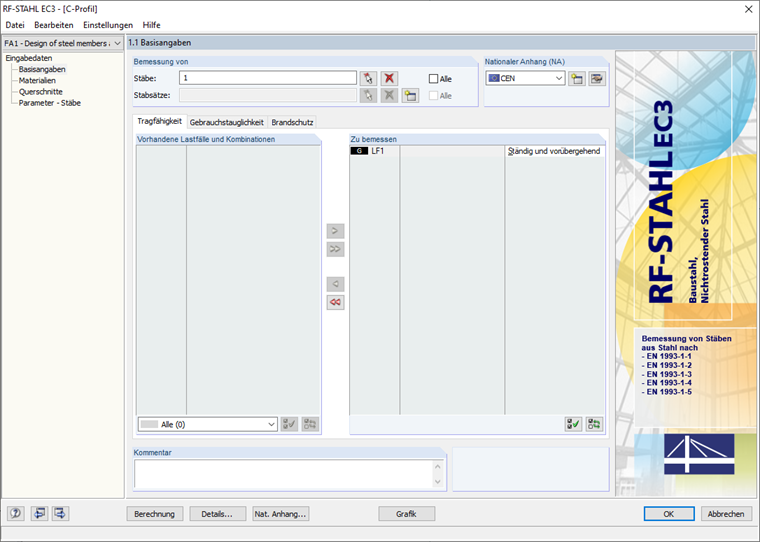
In den Basisangaben sind zunächst der zu bemessende Stab und Lastfall auszuwählen. Als nationaler Anhang wird "CEN" gewählt (Bild 16).

Bild 16 - Basisangaben

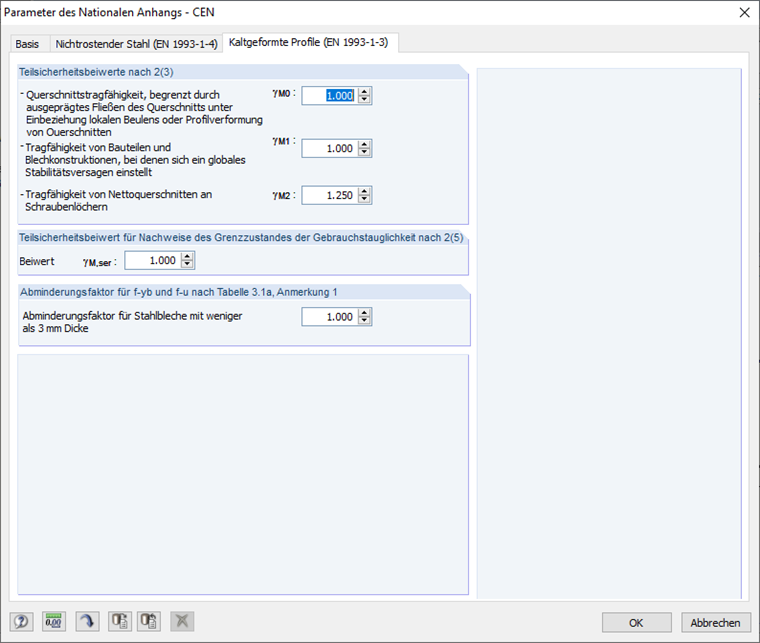
Die Parameter des nationalen Anhangs können im Register "Kaltgeformte Profile (EN 1993-1-3)" des gleichnamigen Fensters eingesehen und ggf. angepasst werden (Bild 17).

Bild 17 - Parameter des nationalen Anhangs

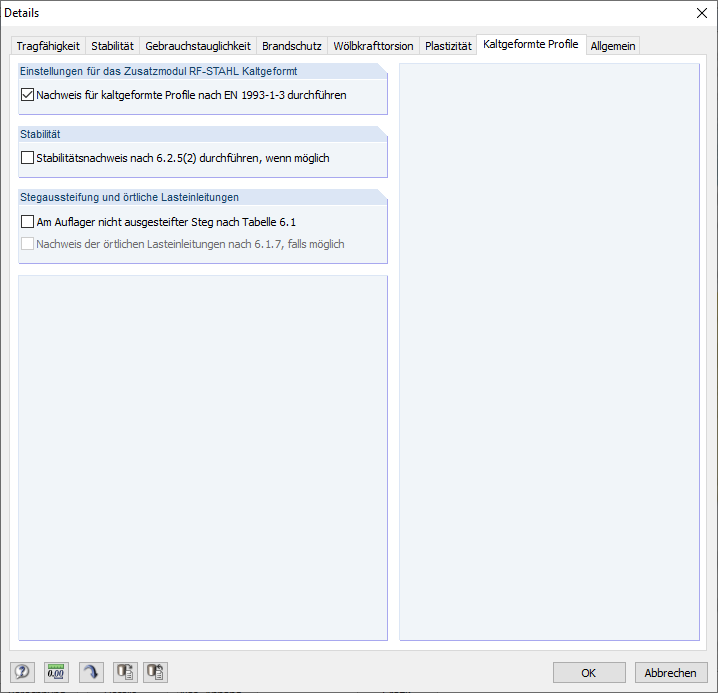
In den Detaileinstellungen ist im Register "Kaltgeformte Profile" der Nachweis für kaltgeformte Profile zu aktivieren (Bild 18).

Bild 18 - Details, Register Kaltgeformte Profile

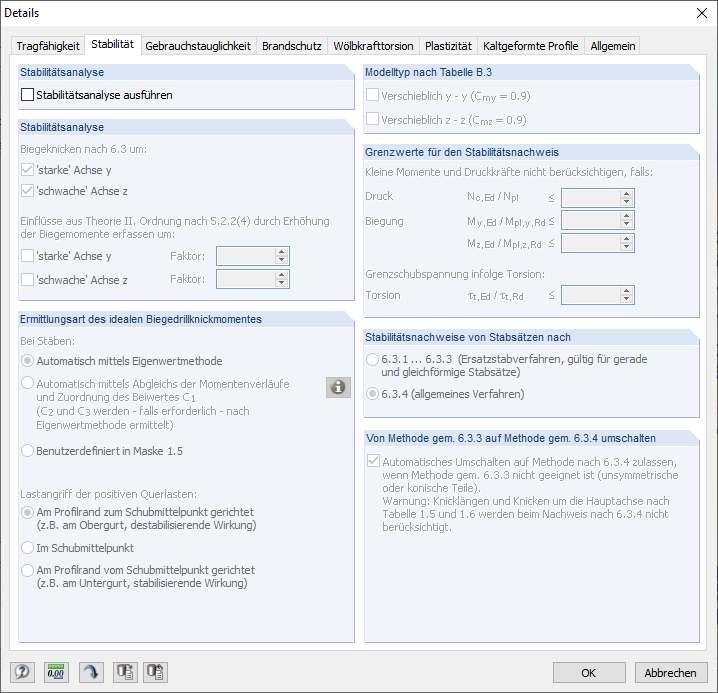
Es soll nur der Querschnittsnachweis geführt werden. Daher ist in den Detaileinstellungen im Register "Stabilität" das Kontrollkästchen "Stabilitätsanalyse ausführen" zu deaktivieren (Bild 19).

Bild 19 - Details, Register Stabilität

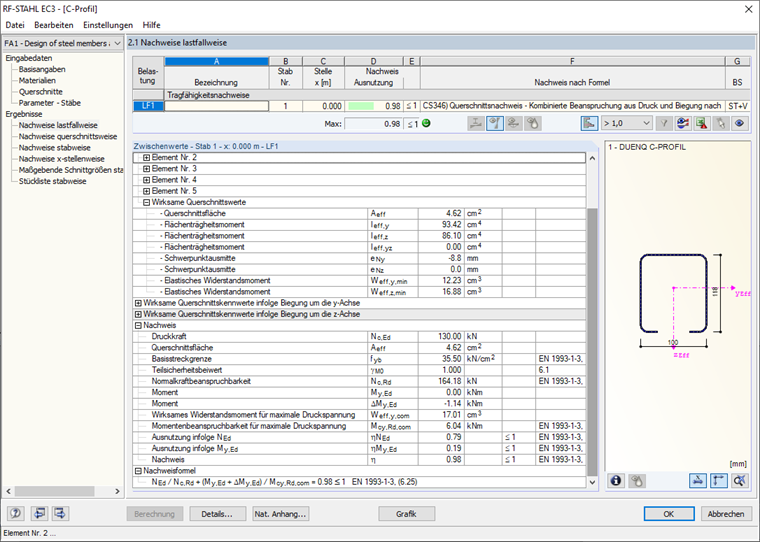
Nach der Berechnung werden in den entsprechenden Ausgabetabellen unter anderem wirksame Querschnittskennwerte infolge Normalkraft N, Biegemoment M_y, Biegemoment M_z, Schnittgrößen und der Gesamtnachweis dargestellt (Bild 20).

Bild 20 - Ergebnisse

Autor

Sonja von Bloh, M.Sc.

Product Engineering & Customer Support

Frau von Bloh bietet im Kundensupport Hilfestellung für unsere Anwender und ist zudem für die Entwicklung des Programms RSECTION sowie für den Stahl- und Aluminiumbau zuständig.

Schlüsselwörter

Querschnittsnachweis Kaltgeformtes Profil

Literatur

[1]	Eurocode 3: Bemessung und Konstruktion von Stahlbauten – Teil 1-3: Allgemeine Regeln - Ergänzende Regeln für kaltgeformte Bauteile und Bleche. Beuth Verlag GmbH, Berlin, 2010
[2]	Eurocode 3: Bemessung und Konstruktion von Stahlbauten – Teil 1-5: Plattenförmige Bauteile. Beuth Verlag GmbH, Berlin, 2010.
[3]	Kuhlmann, U.: Stahlbau-Kalender 2009 - Stabilität, Membrantragwerke. Berlin: Ernst & Sohn, 2009

Downloads

Links

Statik-Software für Stahlbau
Querschnittswerte-Programme

Schreiben Sie einen Kommentar...

0 Kommentieren

3 0

Kontakt

Kontakt zu Dlubal

Haben Sie Fragen oder brauchen Sie einen Rat? Kontaktieren Sie uns über unseren kostenlosen E-Mail-, Chat- bzw. Forum-Support oder nutzen Sie die häufig gestellten Fragen (FAQs) rund um die Uhr.

Häufig gestellte Fragen (FAQs)

Individuelle Frage einreichen

+49 9673 9203 0

[email protected]

Gehe zu
Events
Videos
Modelle
Knowledge Base
Screenshots
Produkt-Features
Häufig gestellte Fragen
Kundenprojekte

Empfohlene Veranstaltungen

Internationale Konferenz für Holzwerkstoff

Seminar/Konferenz 27. März 2023 - 29. März 2023

Pneumatische Membrankonstruktionen in RFEM 6

Formfindung und Berechnung von pneumatischen Membrankonstruktionen in RFEM 6

Webinar 4. April 2023 14:00 - 15:00 CEST

Formfindung und Berechnung pneumatischer Membranstrukturen in RFEM 6

Webinar 6. April 2023 14:00 - 15:00 CEST

BAU 2023

Messe 17. April 2023 - 22. April 2023

Eurocode 3 | Stahlbau nach DIN EN 1993-1-1

Online-Schulung 16. Mai 2023 8:30 - 12:30 CEST

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 23. Mai 2023 8:30 - 12:30 CEST

Stahlsilobemessung in RFEM 6 (USA)

Webinar 21. März 2023 14:00 - 15:00 EDT

Analyse von Stahlkonstruktionen in RFEM 6 und RSTAB 9

Webinar 9. März 2023 14:00 - 15:00 CET

Analyse von Stahlkonstruktionen in RFEM 6 und RSTAB 9

Webinar 7. März 2023 14:00 - 15:00 CET

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 2. März 2023 9:00 - 13:00 CET

Eurocode 3 | Stahltragwerke nach DIN EN 1993-1-1

Online-Schulung 28. Februar 2023 8:30 - 12:30 CET

Stahlbemessung nach CSA S16:19 in RFEM 6 (USA)

Webinar 15. Februar 2023 14:00 - 15:00 EDT

Weitere Veranstaltungen

Videos

KB 001629 | Nachweis eines dünnwandigen, kaltgeformten C-Profils nach EN 1993-1-3

Länge 4:41 min

Webinar | Stahlsilobemessung in RFEM 6

Länge 1:04:40 min

Stabtyp "Flächenmodell"

Länge 0:39 min

Plastisches Materialmodell für die Schweißnahtbemessung

Länge 0:39 min

Nachweise für kaltgeformte Stahlstäbe nach EN 1993-1-3

Länge 0:53 min

KB 001808 | CSA S16:19 Berücksichtigung von Stabilität und Neuer Anhang O.2

Länge 2:18 min

Analyse von Stahlkonstruktionen in RFEM 6 und RSTAB 9

Länge 1:13:12 min

Abschertragfähigkeit der Schrauben

Länge 0:22 min

Komponente Verbindungsplatte

Länge 0:40 min

Weitere Videos

Modelle zum Herunterladen

Beiträge aus der Knowledge Base

Neu

CSA S16:19 Berücksichtigung von Stabilität und Neuer Anhang O.2

Das Verfahren CSA S16:19 Stabilitätseffekte in elastischen Berechnungen in Anhang O.2 ist eine Alternative zum Vereinfachten Stabilitätsanalyseverfahren in Abschnitt 8.4.3. In diesem Beitrag werden die Anforderungen des Anhangs O.2 und die Anwendung in RFEM 6 beschrieben.