Dans l'exemple suivant du Stahlbau-Kalender 2009 [3], la vérification de section d'une poutre à travée simple avec un profilé en C à parois minces et formé à froid est effectuée sous charge d'effort normal. Le section en C est modélisée dans SHAPE-THIN, puis dans RF-/STEEL Cold-Formed Sections.
Système
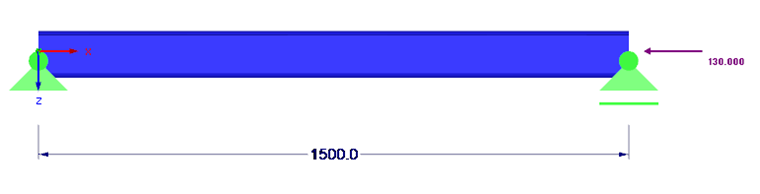
Le système et la charge sont illustrés par la Figure 01.
Matériau
- S 355 EN 10025-2
- E = 210 000 N/mm²
- G = 80 769 N/mm²
- ν = 0,3
- fy = fyb = 355 N/mm²
- γM0 = γM1 = 1,00 (vérification selon CEN)
Dimensions extérieures
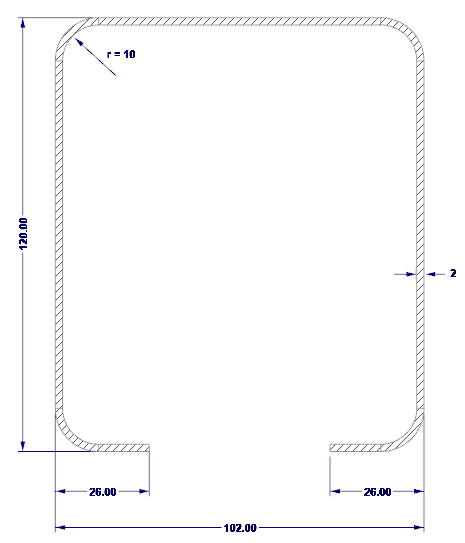
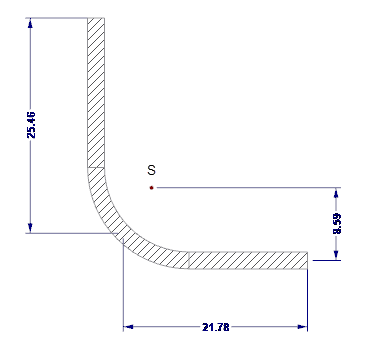
Les dimensions extérieures de la section sont indiquées sur la Figure 02.
- H = 102 mm (hauteur de l'âme)
- b = 120 mm (largeur de la semelle)
- c = 26 mm (longueur des lèvres)
- t = 2 mm (épaisseur du noyau en acier)
Valeur nominale de la largeur
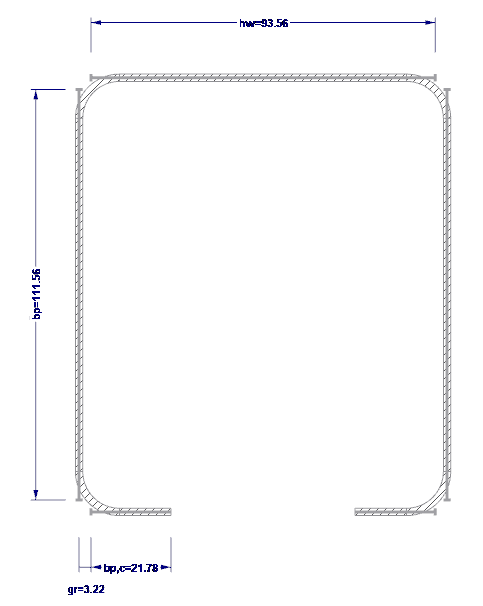
Les valeurs nominales des largeurs droites sont déterminées selon {%}#Refer [1]]], 5.1. Elles sont représentées sur la Figure 03.
Vérification des rapports largeur-épaisseur
Les rapports largeur/épaisseur sont vérifiés selon [1], 5.2(1).
- b / t = 120 / 2 = 60 ≤ 60
- c / t = 26 / 2 = 13 ≤ 50
- H / t = 102 / 2 = 51 ≤ 500
Les rapports largeur-épaisseur sont respectés.
Vérification des dimensions du raidisseur
Les dimensions du raidisseur sont vérifiées selon [1], 5.2(2).
0,2 ≤ c / b = 26 / 120 = 0,22 ≤ 0,6
Les lèvres peuvent être utilisées comme raidisseurs.
Vérification de l'angle entre le raidisseur et l'élément plan
L'angle entre le raidisseur et l'élément plat est de 90°, donc dans la plage de 45° à 135° donnée par [1], 5.5.3.2(1).
Détermination de la section efficace
Pour les sections acier qui ne sont pas doublement symétriques, comprimées et susceptibles de flamber, le centre de gravité de la section efficace se déplace par rapport à la section brute. La force de compression externe s'exerçant sur le centre sur la section brute agit alors de manière excentrée sur la section efficace et un moment fléchissant supplémentaire est généré. Selon [1], les moments supplémentaires résultant du déplacement du centre de gravité doivent être pris en compte. Outre la section efficace pour la contrainte de compression pure, la section efficace pour la contrainte de flexion pure doit ensuite être déterminée.
Détermination de la section efficace en compression pure
Le coefficient est obtenu selon 4.4 (2) de [2] comme suit :
Âme
Le coefficient de voilement est obtenu selon le Tableau 4.1 de [2] comme suit :
L'élancement est obtenu selon 4.4(2) de [2] comme suit :
L'élancement est supérieur à la valeur limite de 0,673 selon [2], 4.4 (2). On doit donc procéder à une réduction.
Le coefficient réducteur est obtenu selon 4.4(2) de [2] comme suit :
La hauteur efficace de l'âme est obtenue selon le Tableau 4.1 de [2] comme suit :
Semelle avec raidisseur de bord
Une première approche de la section efficace du raidisseur est d'abord déterminée selon l'hypothèse que la rigidité du bord agit comme un appui rigide et que σcom,Ed = fyb / γM0.
Semelle
Le coefficient de voilement est obtenu selon le Tableau 4.1 de [2] comme suit :
L'élancement est obtenu selon 4.4(2) de [2] comme suit :
L'élancement est supérieur à la valeur limite de 0,673 selon [2], 4.4 (2). On doit donc procéder à une réduction.
Le coefficient réducteur est obtenu selon 4.4(2) de [2] comme suit :
Selon le Tableau 4.1 [2], la largeur efficace de la semelle est obtenue comme suit :
Rigidité de bord
Le coefficient de voilement est obtenu selon 5.5.3.2 (5) de [1] comme suit :
L'élancement est obtenu selon 4.4(2) de [2] comme suit :
L'élancement est inférieur à la valeur limite de 0,748 selon [1], 4.4 (2). Aucune réduction n'est par conséquent nécessaire, ce qui signifie : ρ = 1,0.
La première approche des résultats de la largeur efficace de [1], Éq. 5.13a à :
Le coefficient réducteur du flambement par distorsion de la section pendant l'utilisation est ensuite déterminé à l'aide de la première approche avérée efficace pour la section en considérant le ressort de translation continu élastique.
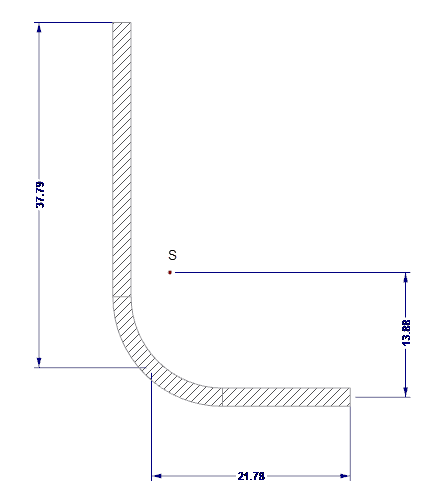
Les propriétés de section efficace des rigidité des bords sont calculées à l'aide de SHAPE-THIN. Cette rigidité est illustrée par la Figure 04.
- As = 122,58 mm2
- Is = 7 130 mm4
- zs = 13,88 mm
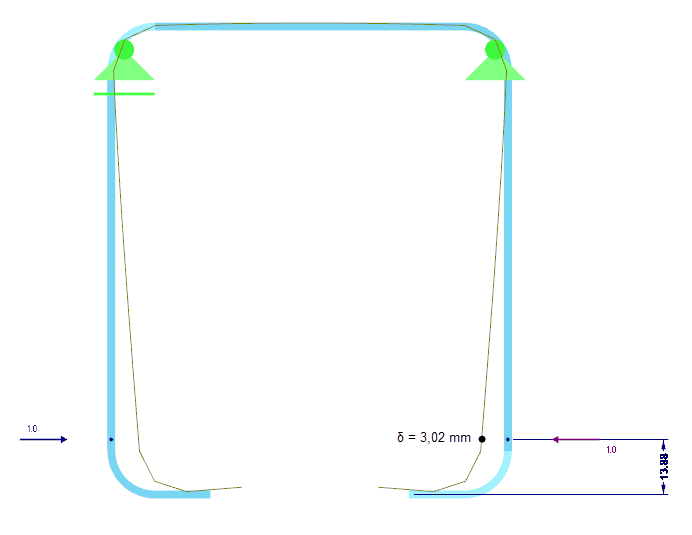
La rigidité de ressort K de la rigidité des bords est déterminée à partir d'un calcul statique pour la section entière. Pour ce faire, une charge distribuée uniformément u agissant dans le centre de gravité du raidisseur efficace est appliquée à la section et la déformation δ correspondante du raidisseur est calculée. Pour une section rectangulaire l/h = t/t = 2/2 mm, on obtient 3,02 mm pour la déformation δ (Figure 05).
La rigidité du ressort par unité de longueur K peut être calculée selon [1], Éq. 5,9 peuvent être calculés comme suit :
La contrainte critique de la rigidité des bords est obtenue à partir de [1], Éq. 5.15 sur :
Le ratio d'élancement est calculé selon [1], Éq. 5.12d à :
Selon 5.5.3.1 (7) de [1], le coefficient réducteur du flambement par distorsion est calculé comme suit :
L’aire de section efficace réduite de la rigidité des bords est obtenue en prenant en compte le flambement par flexion selon [1], Éq. 5.17 à :
Propriétés efficaces de la section en compression pure
La section peut être optimisée à l'aide d'un calcul itératif. On obtient les propriétés de section efficaces suivantes avec deux itérations :
- Surface Aeff = 4,62 cm²
- Distance entre le centre de gravité et l'âme zs, eff = 42,18 mm
- Déplacement du centre de gravité eN,y = zs – * zs,eff = 8,78 mm
Détermination de la section efficace en flexion pure
Âme
L'âme est soumise à une traction et est donc parfaitement efficace.
Semelle avec raidisseur de bord
Une première approche de la section efficace du raidisseur est d'abord déterminée selon l'hypothèse que la rigidité du bord agit comme un appui rigide et que σcom,Ed = fyb / γM0.
Semelle
Le coefficient de voilement est obtenu selon le Tableau 4.1 de [2] comme suit :
L'élancement est obtenu selon 4.4(2) de [2] comme suit :
L'élancement est inférieur à la valeur limite de 0,856 selon [2], 4.4 (2). Aucune réduction n'est par conséquent nécessaire.
Selon le Tableau 4.1 [2], les largeurs efficaces sont obtenues comme suit :
Rigidité de bord
Le coefficient de voilement est obtenu selon 5.5.3.2 (5) de [1] comme suit :
L'élancement est obtenu selon 4.4(2) de [2] comme suit :
L'élancement est inférieur à la valeur limite de 0,748 selon [1], 4.4 (2). Aucune réduction n'est par conséquent nécessaire, ce qui signifie : ρ = 1,0.
La première approche des résultats de la largeur efficace de [1], Éq. 5.13a à :
Le coefficient réducteur du flambement par distorsion de la section pendant l'utilisation est ensuite déterminé à l'aide de la première approche avérée efficace pour la section en considérant le ressort de translation continu élastique.
Les propriétés de section efficace des rigidité des bords sont calculées à l'aide de SHAPE-THIN. Cette rigidité est illustrée par la Figure 06.
- As = 97,92 mm2
- Is = 6 271 mm4
- zs = 8,59 mm
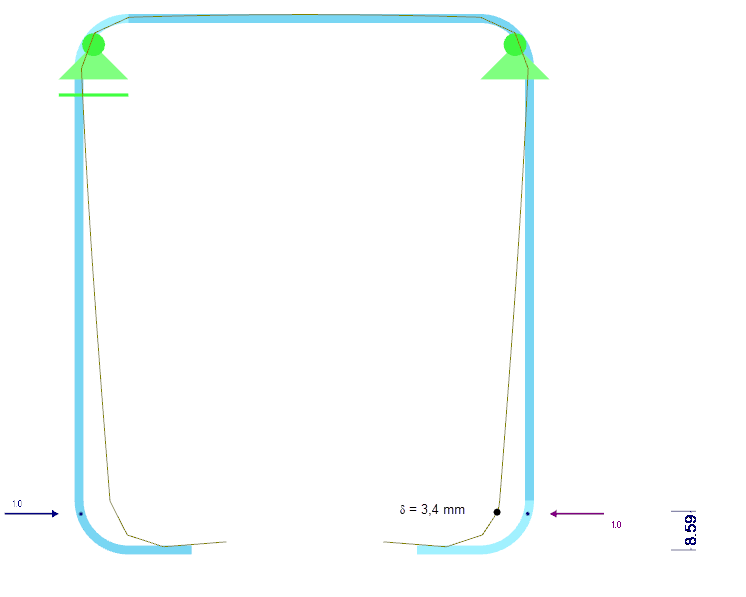
La rigidité de ressort K de la rigidité des bords est déterminée à partir d'un calcul statique pour la section entière. Pour ce faire, une charge distribuée uniformément u agissant dans le centre de gravité du raidisseur efficace est appliquée à la section et la déformation δ correspondante du raidisseur est calculée. Pour une section rectangulaire l/h = t/t = 2/2 mm, on obtient 3,4 mm pour la déformation δ (Figure 07).
La rigidité du ressort par unité de longueur K peut être calculée selon [1], Éq. 5,9 peuvent être calculés comme suit :
La contrainte critique de la rigidité des bords est obtenue à partir de [1], Éq. 5.15 sur :
Le ratio d'élancement est calculé selon [1], Éq. 5.12d à :
Selon 5.5.3.1 (7) de [1], le coefficient réducteur du flambement par distorsion est calculé comme suit :
L'aire de section efficace réduite de la rigidité des bords est obtenue en prenant en compte le flambement par flexion selon {%}#Refer [1]]], Éq. 5.17 à :
Propriétés efficaces de la section en flexion pure
Toutes les parties de section sont efficaces et aucune itération n'est donc nécessaire.
- Surface Aeff = 6,86 cm²
- Module de section Weff, y = 17,01 cm³
Vérification de la section : contrainte combinée issue de la compression et de la flexion
La résistance à la compression pure est calculée selon 6.1.3 (1) de [1] comme suit :
La résistance à la flexion pure est calculée selon 6.1.4.1 (1) de [1] comme suit :
Le moment additionnel résultant du déplacement du centre de gravité est déterminé selon 6.1.9 (2) de [1] comme suit :
La vérification de la charge combinée de compression et de flexion selon 6.1.9 (1) de [1] permet d'obtenir le résultat suivant :
La vérification est ainsi effectuée.
Modélisation de la section en C formée à froid dans SHAPE-THIN
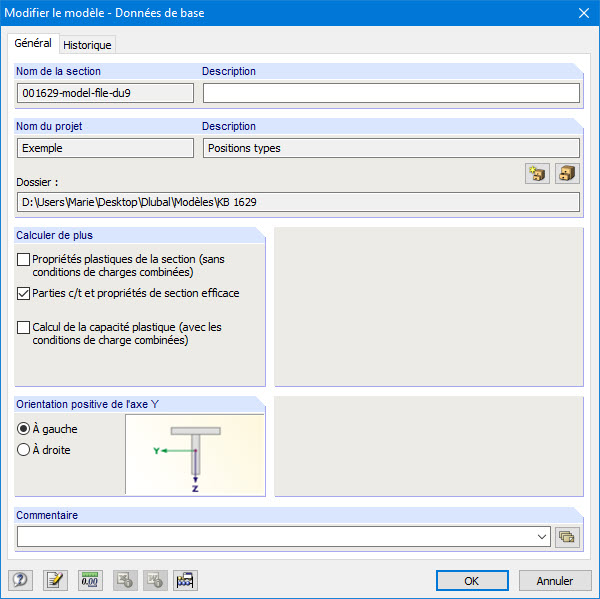
SHAPE-THIN permet de modéliser les sections quelconques formées à froid. La case « Parties c/t et propriétés de la section efficace » doit être cochée dans les données de base (Figure 08).
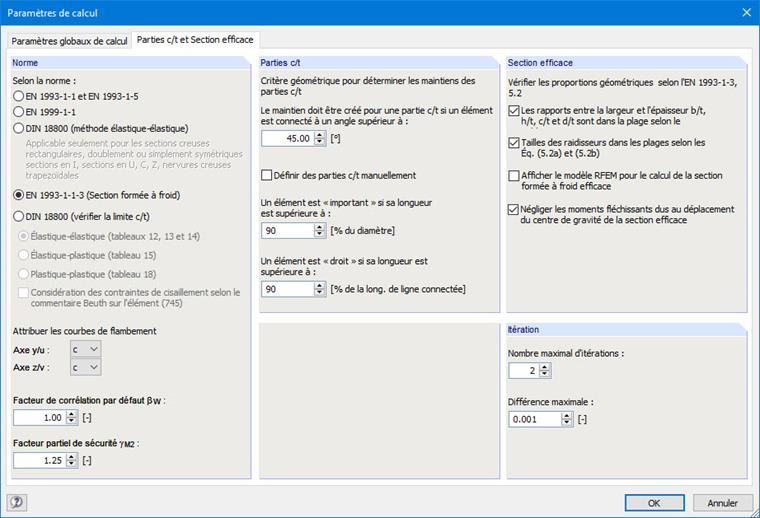
Il faut alors sélectionner l'option « EN 1993-1-3 (section formée à froid) » dans l'onglet « Parties c/t et section efficace » (Figure 09) des paramètres de calcul.
La section efficace doit être déterminée de manière distincte pour la compression pure et pour la flexion pure. Pour ce faire, la case « Ne pas considérer les moments additionnels issus du déplacement du centre de gravité » doit être cochée.
Dans l'exemple traité ici, deux itérations ont été utilisées pour le calcul afin que deux itérations soient également définies dans SHAPE-THIN.
Les conditions géométriques mentionnées dans {%}#Refer [2]]], 5.2 pour l'applicabilité de la norme peuvent être contrôlées éventuellement. Pour ce faire, cochez les cases correspondantes.
Les éléments de la section doivent d’abord avoir été saisis. Les valeurs nominales des largeurs plates sont habituellement générées automatiquement à partir des conditions géométriques, mais peuvent également être définies dans le tableau « 1.7 Valeurs nominales des largeurs plates selon l'EN 1993-1-3 » (Figure 10) ou dans la boîte de dialogue correspondante.
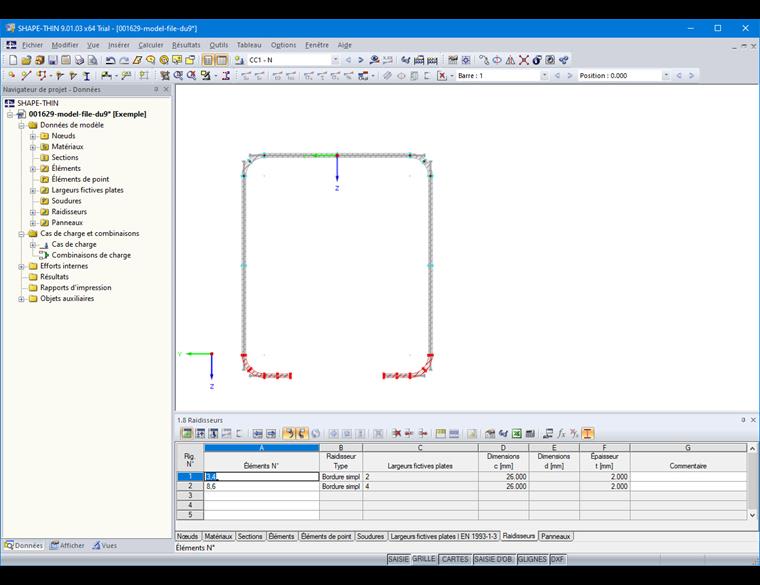
Les raidisseurs peuvent ensuite être définis dans le Tableau « 1.8 Raidisseurs » ou dans la boîte de dialogue correspondante (Figure 11).
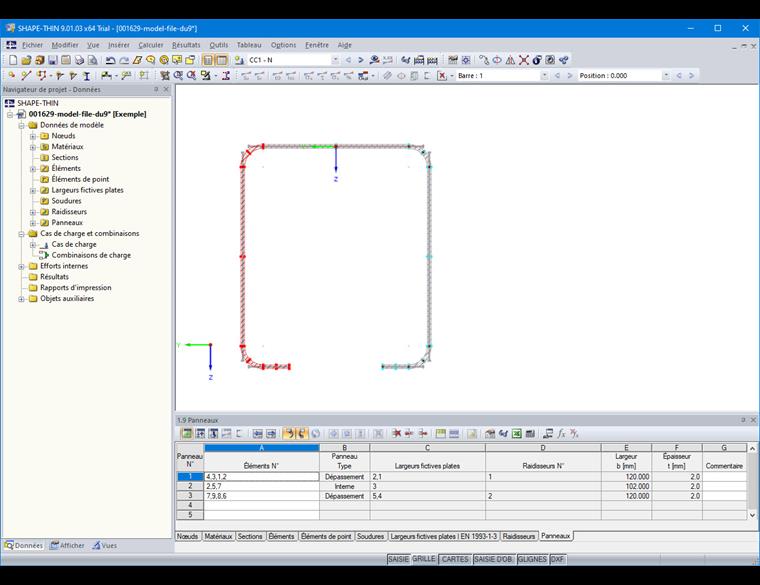
De plus, la plaque doit en outre être entrée dans le Tableau « 1.9 Plaque » (Figure 12) ou dans la boîte de dialogue correspondante. Pour ce faire, sélectionnez les éléments du panneau. Les raidisseurs dans le panneau sont identifiés automatiquement.
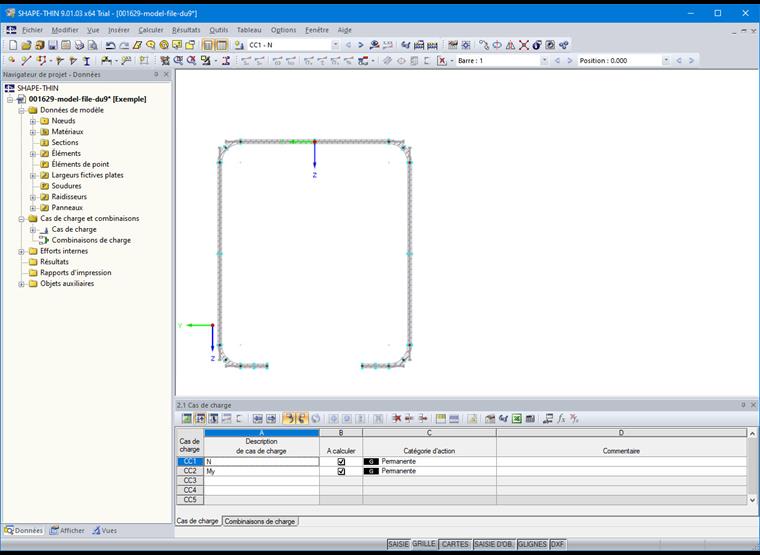
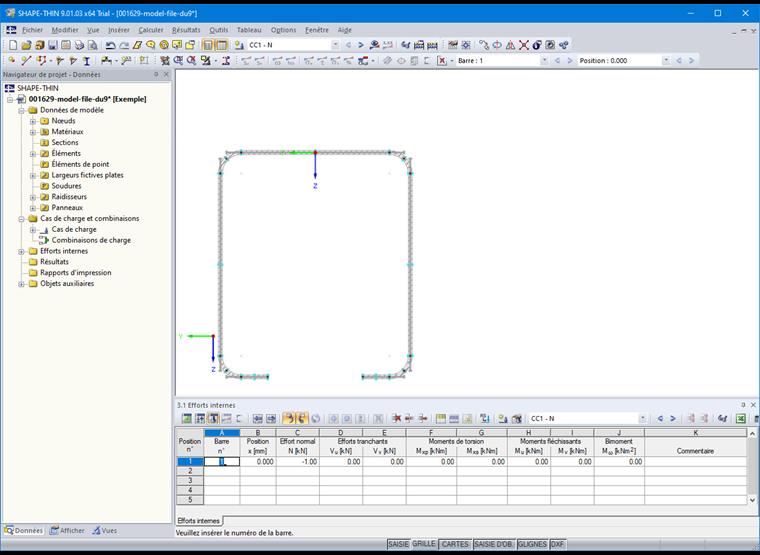
Un cas de charge pour les forces de compression et de flexion est en outre créé dans le Tableau « 2.1 Cas de charge » (Figure 13).
Les efforts internes doivent ensuite être rentrés dans le tableau « 3.1 Efforts internes » ou dans la boîte de dialogue correspondante (Figure 14).
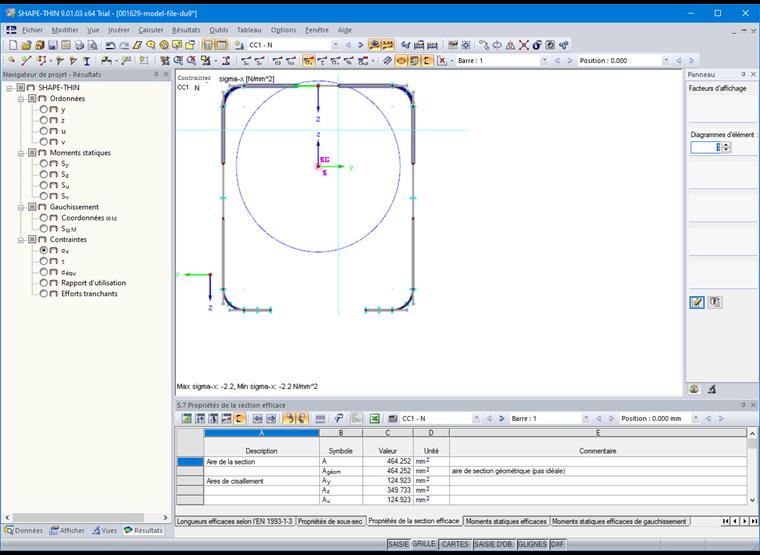
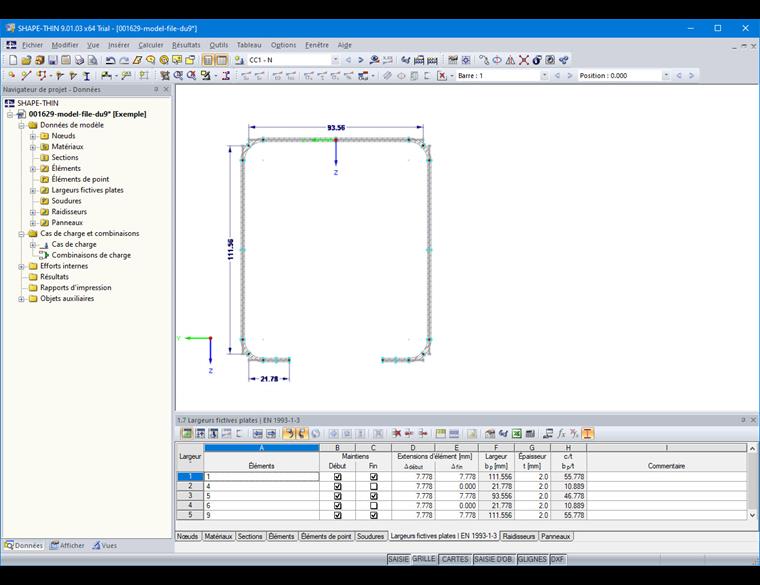
Les résultats de la section efficace sont disponibles en cliquant sur le bouton « Longueurs efficaces » (Figure 15).
Vérification de la section en C formée à froid dans RF-/STEEL Cold-Formed Sections
Les profilés formés à froid peuvent être calculés selon [1] et [2] à l'aide de l'extension de module RF-/STEEL Cold-Formed Sections.
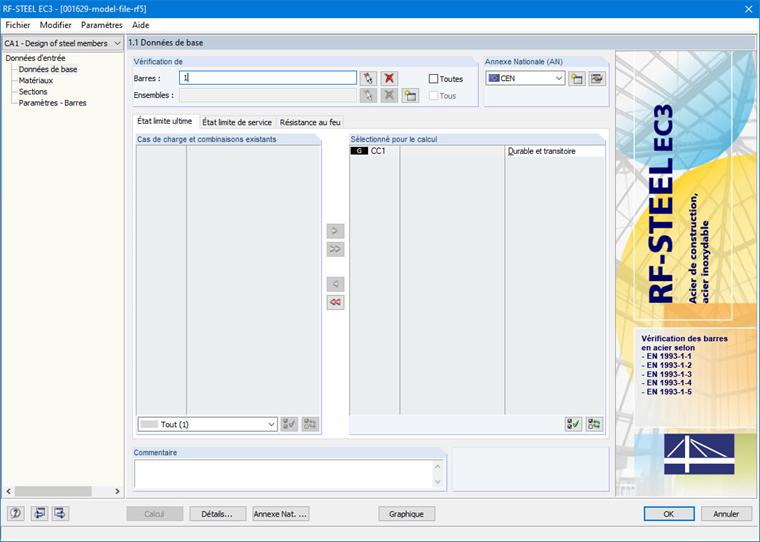
La barre et le cas de charge à calculer doivent tout d'abord être sélectionnés dans les Données de base. L'Annexe Nationale devant être définie est CEN (Figure 16).
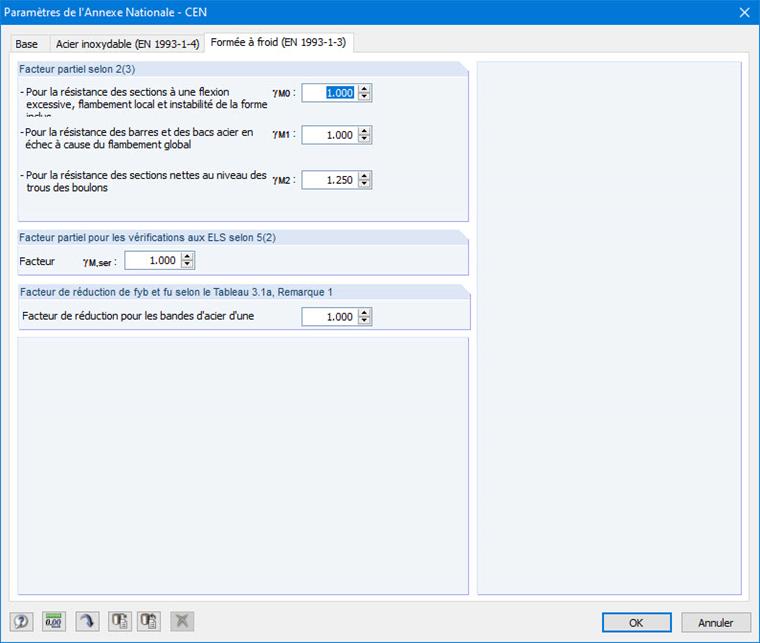
Les paramètres de l'Annexe Nationale peuvent être consultés et, le cas échéant, modifiés dans l'onglet « Section formée à froid (EN 1993-1-3) » de la fenêtre correspondante (Figure 17).
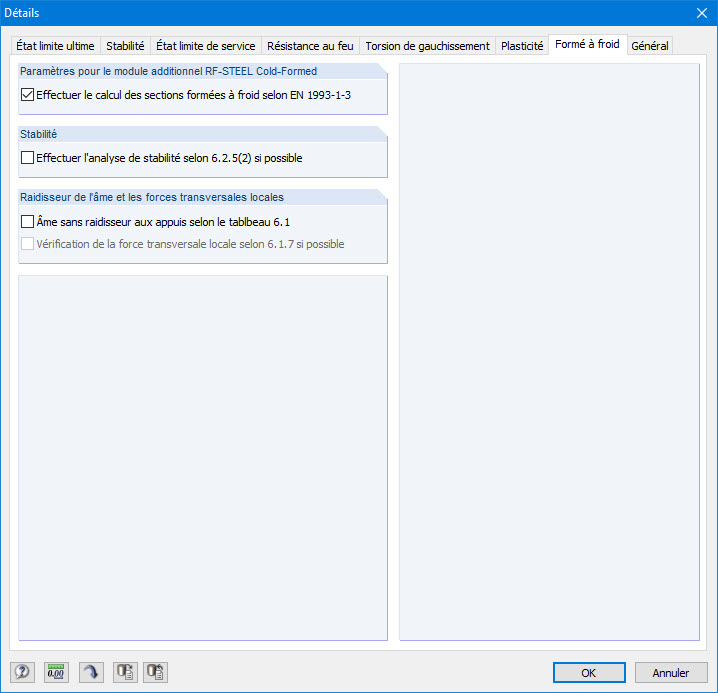
La vérification des sections formées à froid peut être activée dans l'onglet « Sections formées à froid » des paramètres détaillés (Figure 18).
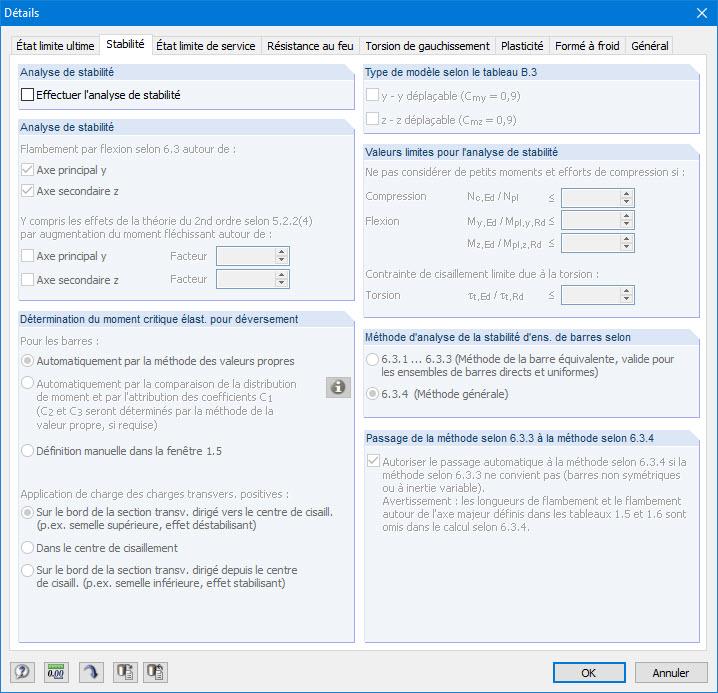
Seule la vérification de la section doit être effectuée. La case « Effectuer l'analyse de stabilité » de l'onglet « Stabilité » des paramètres détaillés doit donc être décochée (Figure 19).
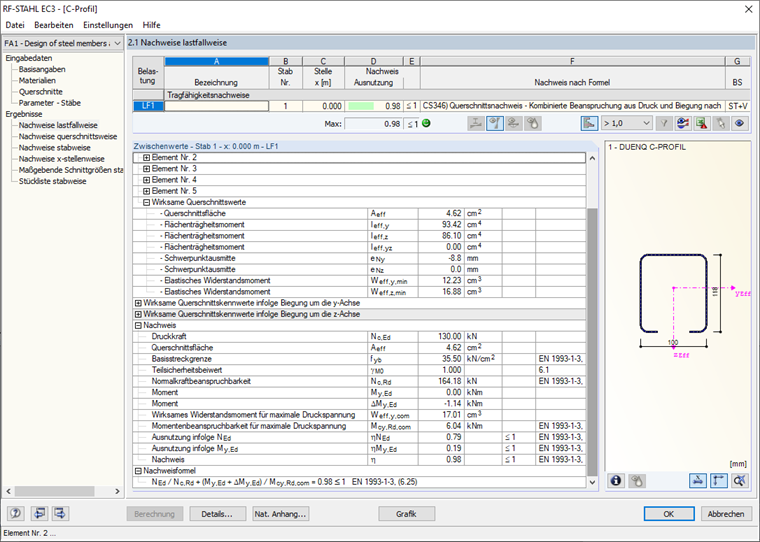
Après le calcul, les tableaux de sortie correspondants contiennent notamment les propriétés de la section efficace dues à l'effort normal N, au moment fléchissant My, au moment fléchissant Mz, aux efforts internes et à l'ensemble de la vérification (Figure 20).