Теоретическая основа
Метод спектрального анализа определяет модальный ответ для каждой собственной частоты с использованием заданного спектра ответа. В сложных системах может возникнуть множество собственных форм, которые необходимо учитывать. Следовательно, последующее суммирование может быть сложным, поскольку на практике никогда не все собственные колебания не проявляются одновременно в полной мере. Чтобы учитывать этот факт в расчетах, отдельные модальные ответы суммируются квадратично. Европейским нормативом EN 1998-1 предлагаются два правила для этого: метод корня суммы квадратов (правило SRSS) и метод полной квадратичной комбинации (правило CQC) [1].
Применение этих правил обычно дает реалистичные и экономичные результаты по сравнению с простой суммой. Однако при суммировании теряются направление воздействия, а следовательно, и знаки результатов. В результате, результаты всегда указываются как максимальные значения в положительном и отрицательном направлениях. Связанные внутренние усилия, например, момент, соответствующий максимальной нормальной силе, теряются. Это должно быть устранено путем модификации правил SRSS и CQC: формулы записываются не в виде корня, а как линейная комбинация. Это правило было введено профессором-доктором-инженером К. Катцем [2] и показано на примере правила SRSS ниже.
Сравнение результатов на примере
Воздействие эквивалентной линейной комбинации будет объяснено на примере простой двухмерной стальной конструкции. Рассматриваются три внутренних усилия: нормальная сила N, поперечная сила Vz и момент My. Для иллюстрации используется модуль RF-DYNAM Pro - замещающие нагрузки. Поведение в RF-DYNAM Pro - вынужденные колебания идентично.
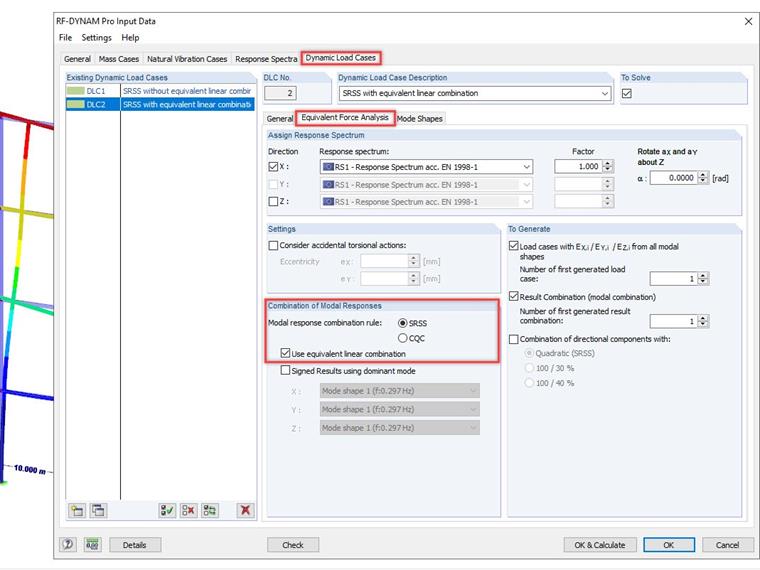
Рассчитываются четыре собственные формы исключительно в X-направлении и используется спектр реакции, основанный на EN 1998-1. Активация эквивалентной линейной комбинации и выбор правила комбинации выполняются на вкладке "Методы с эквивалентными силами" в разделе "Динамические случаи нагрузки" [3].
Результаты отдельных модальных ответов исследуются, например, в узле номер 5 (на элементе номер 6 → левая сторона) и приведены в следующей таблице.
| Ответ от собственной формы 1 | Ответ от собственной формы 2 | Ответ от собственной формы 3 | Ответ от собственной формы 6 | |
|---|---|---|---|---|
| Нормальная сила N | 1,361 кН | -0,246 кН | 0,815 кН | -2,322 кН |
| Поперечная сила V | 0,480 кН | -1,635 кН | -0,556 кН | 1,546 кН |
| Момент M | -2,400 кНм | 8,174 кНм | 2,781 кНм | -7,732 кНм |
С применением стандартного правила SRSS получаются следующие значения.
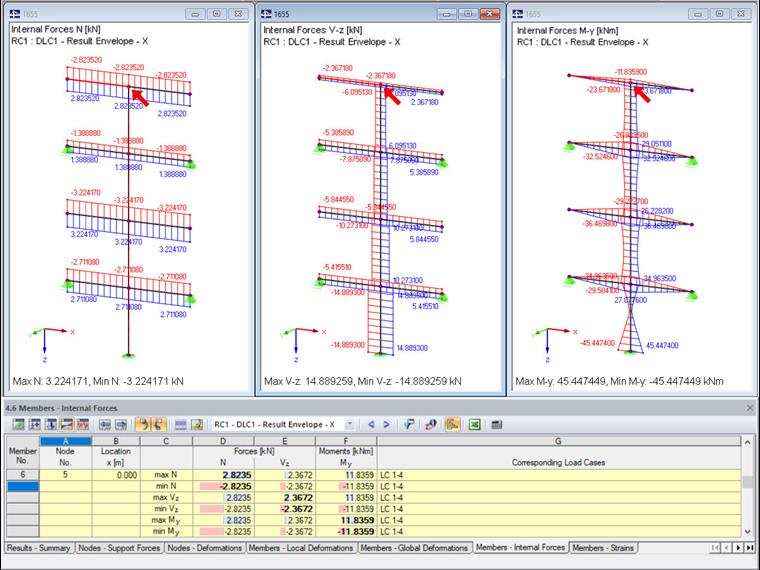
Для оценки этих результатов в RFEM рассматривается сформированная комбинация результатов. Максимальные результаты представлены на графике и в таблице "4.6 Стержни - Внутренние усилия".
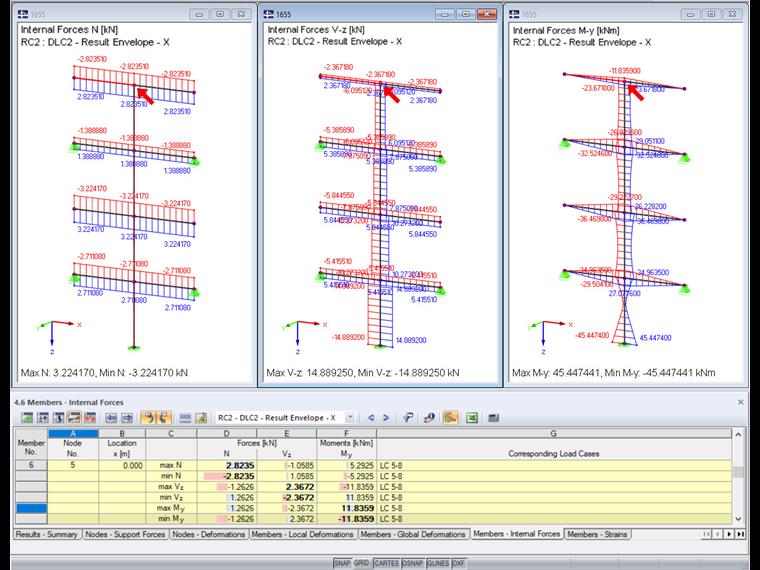
Теперь внутренние усилия рассчитываются с модифицированным правилом SRSS. Эквивалентная линейная комбинация позволяет рассчитать внутренние усилия отдельно для каждого максимального воздействия. Для максимальной нормальной силы получаются следующие внутренние усилия.
Этот подход должен быть проведен для всех воздействий. Результирующие внутренние усилия представлены в следующей таблице.
| Нормальная сила N | Поперечная сила V | Момент M | |
|---|---|---|---|
| Max N | 2,823 кН | -1,058 кН | 5,292 кНм |
| Min N | -2,823 кН | 1,058 кН | -5,292 кНм |
| Max V | -1,263 кН | 2,367 кН | -11,836 кНм |
| Min V | 1,263 кН | -2,367 кН | 11,836 кНм |
| Max M | 1,263 кН | -2,367 кН | 11,836 кНм |
| Min M | -1,263 кН | 2,367 кН | -11,836 кНм |
График в RFEM по-прежнему показывает только максимальные внутренние усилия. Однако в таблице видны различия.
Заключение и дополнительные возможности использования
Было показано, что связанные внутренние усилия могут быть сохранены с использованием эквивалентной линейной комбинации. Если это правило комбинирования используется и импортируется в модули расчета, обычно получаются более экономичные результаты. Пример использования в дополнительном модуле можно найти по ссылкам.
Также возможно использование эквивалентной линейной комбинации вне модуля RF-/DYNAM Pro. Она может быть активирована в параметрах расчета для любой комбинации результатов, если используется правило SRSS. Для правила CQC метод аналогичен. Однако правило CQC может быть использовано только для тех комбинаций результатов, в которых используются исключительно случаи нагрузки категории "Землетрясение", и параметры правила CQC сами определены в случае нагрузки.
Вопрос о том, какое правило комбинирования следует использовать для расчета, остается нерешённым. Правило CQC всегда дает более точные результаты, так как оно может учитывать значимость близко расположенных собственных форм. Правило SRSS может использоваться в ручных расчетах. В компьютерных расчетах, например, в RFEM и RF-DYNAM Pro, рекомендуется использовать правило CQC, записанное как линейная комбинация, поскольку это всегда дает правильные и экономичные результаты. Повышенная сложность расчета пренебрежимо мала.