Teoretické pozadí
Metoda odezvových spekter určuje modální odezvu pro každou vlastní frekvenci na základě definovaného odezvového spektra. U komplexních systémů může docházet k tomu, že se musí zohlednit velké množství vlastních tvarů. Následné skládání se pak stává obtížným, protože ve skutečnosti všechny vlastní kmitání nikdy nemohou nastat současně v plném rozsahu. Aby byla tato skutečnost zohledněna při výpočtu, jsou jednotlivé modální odezvy skládány kvadraticky. V evropské normě relevantní pro dimenzování EN 1998-1 jsou pro tento účel uvedena dvě pravidla: metoda kvadratickým součtem odmocnin (SRSS-pravidlo) a metoda úplné kvadratické kombinace (CQC-pravidlo) [1].
Použití těchto pravidel obvykle poskytuje realistické a ekonomické výsledky ve srovnání s jednoduchým součtem. Při skládání se však ztrácí směr buzení a tím i znaménka výsledků. Z toho vyplývá, že výsledky jsou vždy uváděny jako maximální hodnoty jak v pozitivním, tak i negativním směru. Příslušné vnitřní síly, například moment v místě maximální normálové síly, se při tom ztrácejí. Tento problém má řešit modifikace SRSS a CQC-pravidla: Formule jsou místo odmocniny zapsány jako lineární kombinace. Toto pravidlo zavedl prof. Dr. -Ing. C. Katz [2] a je následující příklad SRSS-pravidla.
Srovnání výsledků na příkladu
Účinek ekvivalentní lineární kombinace bude ilustrován na jednoduché dvourozměrné ocelové konstrukci. Při tom budou zkoumány tři vnitřní síly: normálová síla N, smyková síla Vz a moment My. Pro ilustraci bude použit modul RF-DYNAM Pro - Náhradní zatížení. Chování v RF-DYNAM Pro - Vynucené kmitání je totožné.
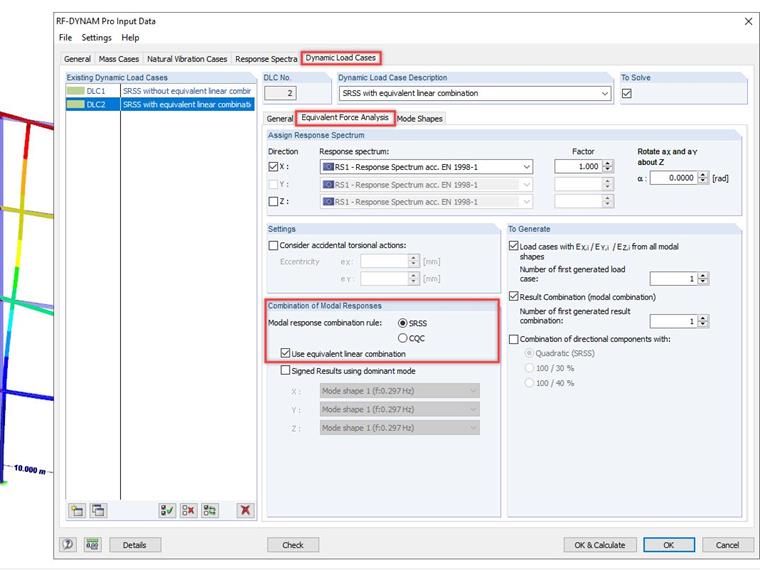
Budou počítány čtyři vlastní tvary výhradně ve směru X a použito odpovídající spektrum na základě EN 1998-1. Aktivace ekvivalentní lineární kombinace a výběr pravidla pro kombinaci probíhá v záložce "Metoda s ekvivalentními silami" pod "Dynamickými zatěžovacími případy" [3].
Výsledky jednotlivých modálních odezev budou zkoumány například v uzlu číslo 5 (na prutu číslo 6 → levá strana) a uvedeny v následující tabulce.
| Odezva z vlastního tvaru 1 | Odezva z vlastního tvaru 2 | Odezva z vlastního tvaru 3 | Odezva z vlastního tvaru 6 | |
|---|---|---|---|---|
| Normálová síla N | 1,361 kN | -0,246 kN | 0,815 kN | -2,322 kN |
| Smyková síla V | 0,480 kN | -1,635 kN | -0,556 kN | 1,546 kN |
| Moment M | -2,400 kNm | 8,174 kNm | 2,781 kNm | -7,732 kNm |
Pomocí standardního SRSS-pravidla vyplývají následující hodnoty.
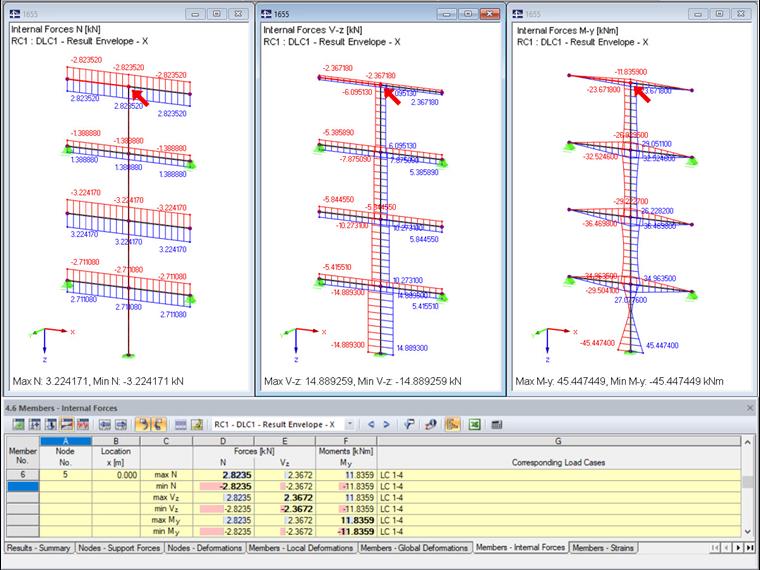
Abychom tyto výsledky v RFEM vyhodnotili, bude zkoumána generovaná kombinace výsledků. Maximální výsledky jsou zobrazeny v grafice i v tabulce "4.6 Pruty - průřezy".
Nyní budou vnitřní síly vypočteny pomocí modifikovaného SRSS-pravidla. Pomocí ekvivalentní lineární kombinace budou vnitřní síly počítány odděleně pro každé maximální zatížení. Výsledné vnitřní síly pro maximální normálovou sílu jsou následující.
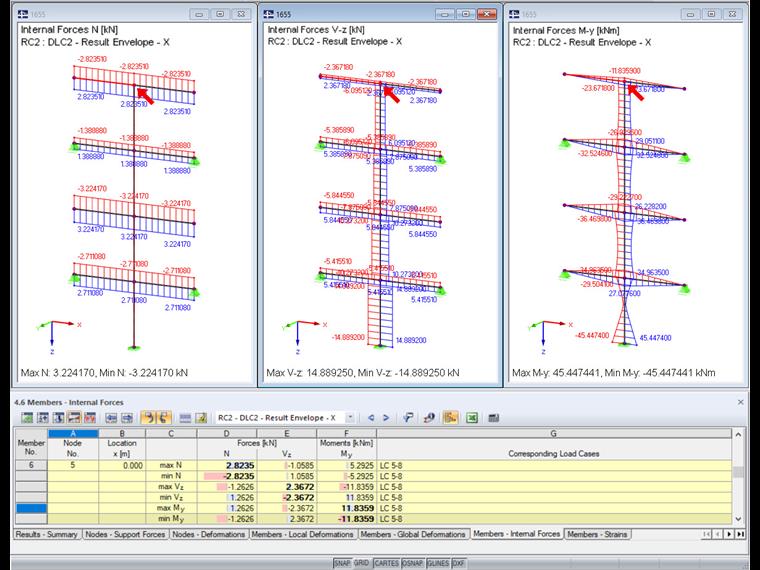
Tento postup musí být nyní proveden pro všechna zatížení. Výsledné vnitřní síly jsou uvedeny v následující tabulce.
| Normálová síla N | Smyková síla V | Moment M | |
|---|---|---|---|
| Max N | 2,823 kN | -1,058 kN | 5,292 kNm |
| Min N | -2,823 kN | 1,058 kN | -5,292 kNm |
| Max V | -1,263 kN | 2,367 kN | -11,836 kNm |
| Min V | 1,263 kN | -2,367 kN | 11,836 kNm |
| Max M | 1,263 kN | -2,367 kN | 11,836 kNm |
| Min M | -1,263 kN | 2,367 kN | -11,836 kNm |
Grafika v RFEM stále zobrazuje výhradně maximální vnitřní síly. V tabulce jsou však patrné rozdíly.
Závěr a další možnosti použití
Bylo možné ukázat, že přímé vnitřní síly se zachovají použitím ekvivalentní lineární kombinace. Pokud se použije toto pravidlo pro kombinaci a načítá se do dimenzačních modulů, obvykle získáme hospodárnější výsledky. Příklad použití v přídavném modulu je uveden v odkazech.
Je také možné použít ekvivalentní lineární kombinaci mimo modul RF-/DYNAM Pro. Tato možnost může být aktivována v parametrech výpočtu pro libovolnou kombinaci výsledků, pokud se používá SRSS-pravidlo. Pro CQC-pravidlo je postup obdobný. CQC-pravidlo však může být použito pouze pro ty kombinace výsledků, ve kterých se používají pouze zatěžovací případy kategorie Zemětřesení, a které mají parametry CQC-pravidla definované přímo v zatěžovacím případě.
Zůstává otázka nevyřešená, které pravidlo pro kombinaci by mělo být nakonec použito pro dimenzování. CQC-pravidlo vždy poskytuje přesnější výsledky, protože zohledňuje významnost blízkých vlastních tvarů. SRSS-pravidlo může být použito pro ruční výpočty. U počítačově asistovaných výpočtů, například pomocí RFEM a RF-DYNAM Pro, se doporučuje použití CQC-pravidla, zapsaného jako lineární kombinace, protože to v každém případě poskytuje správné a hospodárné výsledky. Zvýšená výpočetní náročnost je zanedbatelná.