Theoretischer Hintergrund
Das Antwortspektrenverfahren ermittelt für jede Eigenfrequenz eine modale Antwort anhand des definierten Antwortspektrums. Bei komplexen Systemen kann es dabei zu einer Vielzahl von zu berücksichtigenden Eigenformen kommen. Die nachfolgende Überlagerung gestaltet sich deshalb als schwierig, weil in der Realität niemals alle Eigenschwingungen in ihrer vollen Größe gleichzeitig auftreten können. Um diese Tatsache in der Berechnung zu berücksichtigen, werden die einzelnen Modalantworten quadratisch überlagert. In der europäischen bemessungsrelevanten Norm EN 1998-1 werden dafür zwei Regeln vorgestellt: die Methode der Quadratsummenwurzel (SRSS-Regel) und die Methode der vollständigen quadratischen Überlagerung (CQC-Regel) [1].
Die Anwendung dieser Regeln liefert gewöhnlich realitätsnahe und wirtschaftliche Ergebnisse im Gegensatz zu einer einfachen Addition. Jedoch gehen bei der Überlagerung die Richtung der Erregung und somit die Vorzeichen der Ergebnisse verloren. Daraus resultiert, dass die Ergebnisse immer als Maximalwerte in positiver sowie in negativer Richtung angegeben werden. Zugehörige Schnittgrößen, also beispielsweise ein zugehöriges Moment bei maximaler Normalkraft, gehen dabei verloren. Dies soll durch eine Modifikation der SRSS- und CQC-Regel umgangen werden: Die Formeln werden statt als Wurzel als Linearkombination geschrieben. Diese Regel wurde durch Prof. Dr.-Ing. C. Katz eingeführt [2] und wird nachfolgend am Beispiel der SRSS-Regel gezeigt.
Vergleich der Ergebnisse anhand eines Beispiels
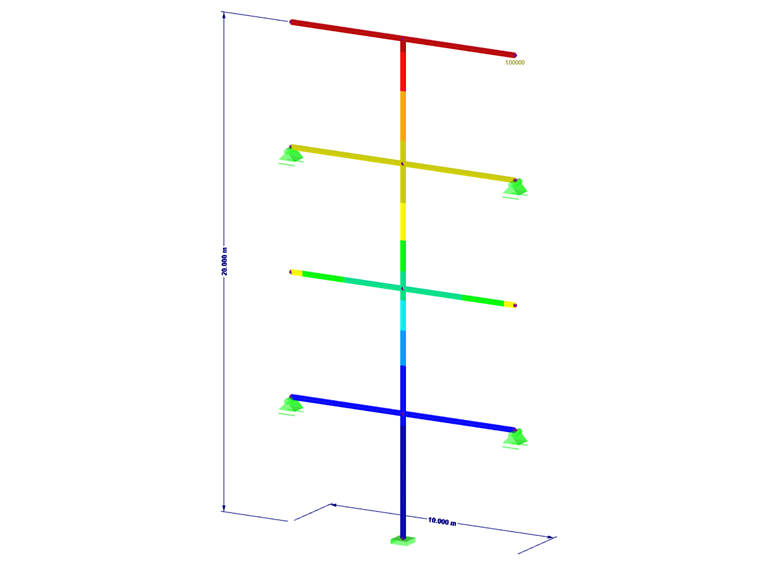
Die Auswirkung der äquivalenten Linearkombination soll an einem einfachen zweidimensionalen Stahltragwerk erläutert werden. Dabei werden drei Schnittgrößen betrachtet: die Normalkraft N, die Schubkraft Vz und das Moment My. Zur Veranschaulichung wird das Modul RF-DYNAM Pro - Ersatzlasten verwendet. Das Verhalten in RF-DYNAM Pro - Erzwungene Schwingungen ist identisch.
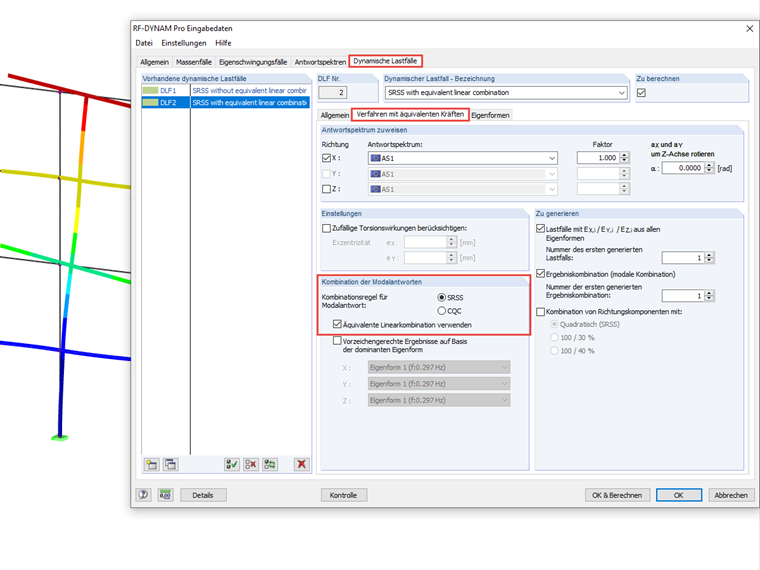
Es werden vier Eigenformen ausschließlich in X-Richtung berechnet und ein Antwortspektrum basierend auf EN 1998-1 verwendet. Die Aktivierung der äquivalenten Linearkombination und die Wahl der Kombinationsregel erfolgt im Reiter "Verfahren mit äquivalenten Kräften" unter "Dynamische Lastfälle" [3].
Die Ergebnisse der einzelnen Modalantworten werden beispielsweise an Knoten Nummer 5 (am Stab Nummer 6 → linke Seite) untersucht und sind in nachfolgender Tabelle gelistet.
| Antwort aus Eigenform 1 | Antwort aus Eigenform 2 | Antwort aus Eigenform 3 | Antwort aus Eigenform 6 | |
|---|---|---|---|---|
| Normalkraft N | 1,361 kN | -0,246 kN | 0,815 kN | -2,322 kN |
| Schubkraft V | 0,480 kN | -1,635 kN | -0,556 kN | 1,546 kN |
| Moment M | -2,400 kNm | 8,174 kNm | 2,781 kNm | -7,732 kNm |
Mit der Standard-SRSS-Regel ergeben sich folgende Werte.
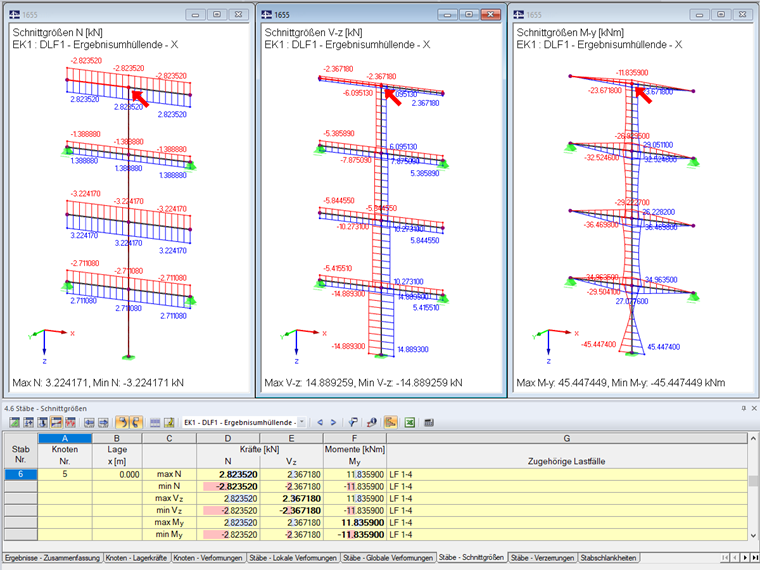
Um diese Ergebnisse in RFEM auszuwerten, wird die generierte Ergebniskombination betrachtet. Die maximalen Ergebnisse werden in der Grafik sowie in der Tabelle "4.6 Stäbe - Schnittgrößen" dargestellt.
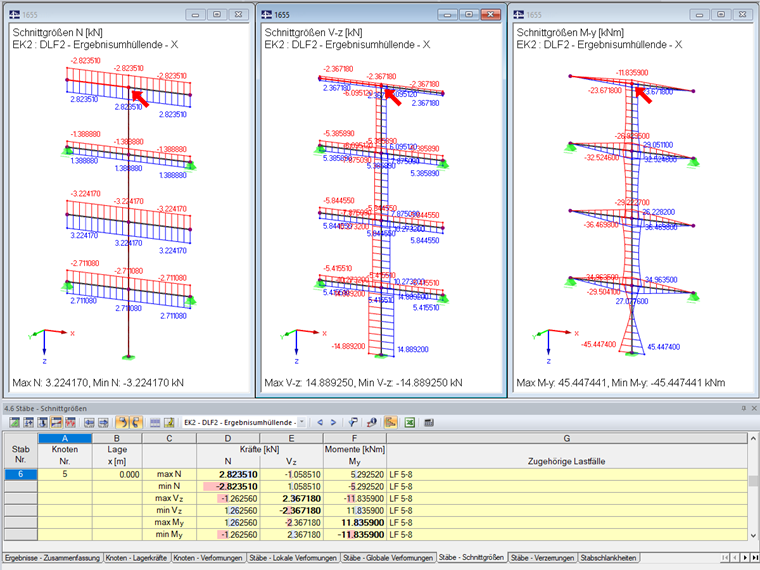
Nun werden die Schnittgrößen mit der modifizierten SRSS-Regel berechnet. Durch die äquivalente Linearkombination werden die Schnittgrößen getrennt für jede maximale Einwirkung berechnet. Es ergeben sich für die maximale Normalkraft folgende Schnittgrößen.
Dieses Vorgehen muss nun für alle Einwirkungen durchgeführt werden. Die resultierenden Schnittgrößen sind in der nachfolgenden Tabelle dargestellt.
| Normalkraft N | Schubkraft V | Moment M | |
|---|---|---|---|
| Max N | 2,823 kN | -1,058 kN | 5,292 kNm |
| Min N | -2,823 kN | 1,058 kN | -5,292 kNm |
| Max V | -1,263 kN | 2,367 kN | -11,836 kNm |
| Min V | 1,263 kN | -2,367 kN | 11,836 kNm |
| Max M | 1,263 kN | -2,367 kN | 11,836 kNm |
| Min M | -1,263 kN | 2,367 kN | -11,836 kNm |
Die Grafik in RFEM zeigt nach wie vor ausschließlich die maximalen Schnittgrößen. In der Tabelle sind hingegen die Unterschiede sichtbar.
Fazit und zusätzliche Verwendungsmöglichkeiten
Es konnte gezeigt werden, dass die zugehörigen Schnittgrößen durch die Verwendung der äquivalenten Linearkombination erhalten bleiben. Wird diese Kombinationsregel verwendet und in den Bemessungsmodulen eingelesen, erhält man meist wirtschaftlichere Ergebnisse. Ein Beispiel für die Verwendung in einem Zusatzmodul findet sich in den Links.
Es ist ebenfalls möglich, die äquivalente Linearkombination außerhalb des Moduls RF-/DYNAM Pro zu verwenden. Diese kann in den Berechnungsparametern für jede beliebige Ergebniskombination aktiviert werden, insofern die SRSS-Regel verwendet wird. Für die CQC-Regel ist das Vorgehen analog. Jedoch kann die CQC-Regel nur für jene Ergebniskombinationen verwendet werden, in denen ausschließlich Lastfälle der Kategorie Erdbeben verwendet und die Parameter der CQC-Regel im Lastfall selbst definiert wurden.
Ungeklärt bleibt die Frage, welche Kombinationsregel schlussendlich für die Bemessung verwendet werden soll. Die CQC-Regel liefert in jedem Fall genauere Ergebnisse, da diese die Relevanz von nahe beieinander liegenden Eigenformen berücksichtigen kann. Die SRSS-Regel kann in Handrechnungen verwendet werden. In computergestützten Berechnungen, beispielsweise mit RFEM und RF-DYNAM Pro, wird die Verwendung der CQC-Regel, geschrieben als Linearkombination, empfohlen, da dies in allen Fällen korrekte und wirtschaftliche Ergebnisse liefert. Der erhöhte Rechenaufwand ist vernachlässigbar klein.