Fondements théoriques
L’analyse du spectre de réponse détermine pour chaque fréquence propre une réponse modale basée sur le spectre de réponse défini. Dans des systèmes complexes, cela peut entraîner un grand nombre de modes propres à considérer. La superposition suivante s’avère complexe, car dans la réalité, toutes les vibrations propres n’apparaissent jamais simultanément dans leur pleine amplitude. Pour en tenir compte dans le calcul, les réponses modales individuelles sont superposées de façon quadratique. La norme européenne EN 1998-1 présente à cet effet deux règles : la méthode de la racine carrée de la somme des carrés (règle SRSS) et la méthode de superposition quadratique complète (règle CQC) [1].
L’application de ces règles permet généralement des résultats réalistes et économiques, contrairement à une simple addition. Cependant, lors de la superposition, la direction de l’excitation et donc les signes des résultats sont perdus. Il en résulte que les résultats sont toujours donnés comme valeurs maximales dans les deux sens positif et négatif. Les efforts internes associés, tels qu’un moment associé à un effort normal maximal, sont alors perdus. Pour éviter cela, une modification des règles SRSS et CQC est recommandée : les formules sont écrites sous forme de combinaison linéaire au lieu de racine. Cette règle a été introduite par le Prof. Dr.-Ing. C. Katz [2] et est démontrée ci-dessous à l’aide de la règle SRSS.
Comparaison des résultats à l’aide d’un exemple
L’effet de la combinaison linéaire équivalente sera expliqué à l’aide d’une structure en acier bidimensionnelle simple. Trois efforts internes sont considérés : l’effort normal N, l’effort tranchant Vz et le moment My. Le module additionnel RF-DYNAM Pro - Equivalent Loads est utilisé pour illustrer cela. Le comportement dans RF-DYNAM Pro - Forced Vibrations est identique.
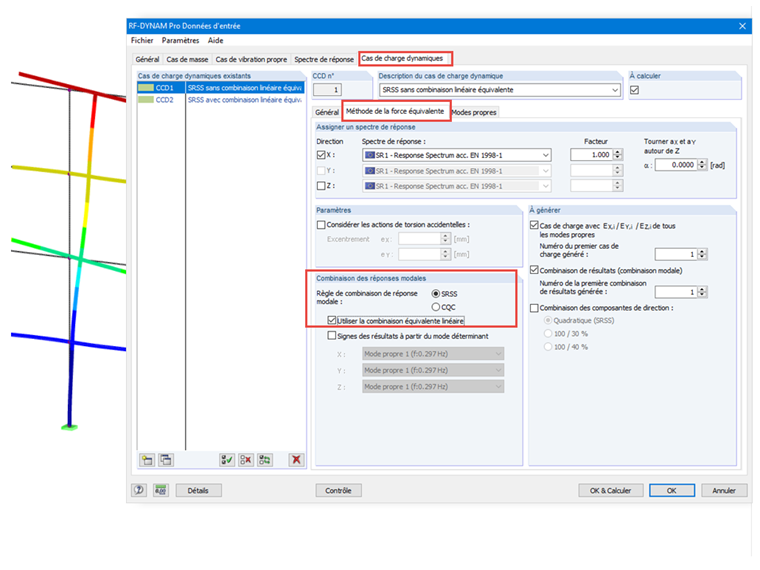
Quatre modes propres sont calculés exclusivement dans la direction X et un spectre de réponse basé sur EN 1998-1 est utilisé. L’activation de la combinaison linéaire équivalente et le choix de la règle de combinaison se font dans l’onglet « Méthode des forces équivalentes » sous « Cas de charge dynamique » [3].
Les résultats des réponses modales individuelles sont examinés, par exemple, au nœud numéro 5 (sur la barre numéro 6 → côté gauche), et listés dans le tableau suivant.
| Réponse du mode propre 1 | Réponse du mode propre 2 | Réponse du mode propre 3 | Réponse du mode propre 6 | |
|---|---|---|---|---|
| Force normale N | 1,361 kN | -0,246 kN | 0,815 kN | -2,322 kN |
| Force tranchante V | 0,480 kN | -1,635 kN | -0,556 kN | 1,546 kN |
| Moment M | -2,400 kNm | 8,174 kNm | 2,781 kNm | -7,732 kNm |
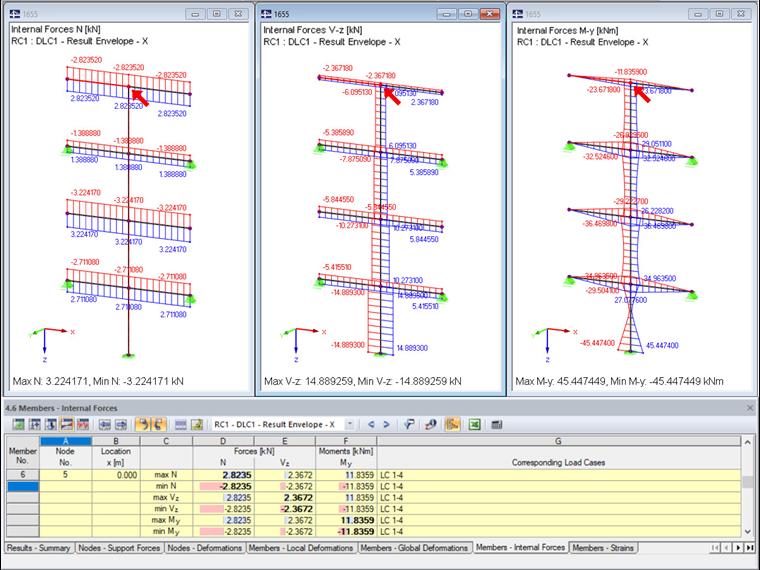
Avec la règle SRSS standard, les valeurs suivantes sont obtenues.
Pour évaluer ces résultats dans RFEM, la combinaison de résultats générée est examinée. Les résultats maximaux sont affichés dans le graphique ainsi que dans le tableau « 4.6 Barres - Efforts internes ».
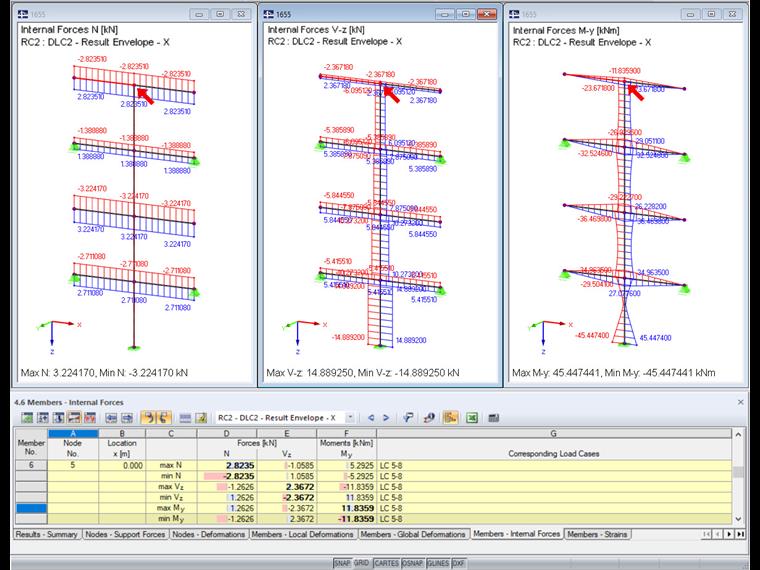
Maintenant, les efforts internes sont calculés avec la règle SRSS modifiée. Grâce à la combinaison linéaire équivalente, les efforts internes sont calculés séparément pour chaque effet maximal. Les efforts internes suivants sont obtenus pour l’effort normal maximal.
Cette procédure doit être exécutée pour toutes les actions. Les efforts internes résultants sont présentés dans le tableau suivant.
| Effort normal N | Effort tranchant V | Moment M | |
|---|---|---|---|
| Max N | 2,823 kN | -1,058 kN | 5,292 kNm |
| Min N | -2,823 kN | 1,058 kN | -5,292 kNm |
| Max V | -1,263 kN | 2,367 kN | -11,836 kNm |
| Min V | 1,263 kN | -2,367 kN | 11,836 kNm |
| Max M | 1,263 kN | -2,367 kN | 11,836 kNm |
| Min M | -1,263 kN | 2,367 kN | -11,836 kNm |
Le graphique dans RFEM continue de montrer uniquement les efforts internes maximaux. Le tableau, cependant, montre les différences.
Conclusion et autres applications possibles
Nous avons démontré que les efforts internes associés sont préservés grâce à l’utilisation de la combinaison linéaire équivalente. Si cette règle de combinaison est utilisée et intégrée dans les modules, on obtient généralement des résultats plus économiques. Un exemple d’utilisation dans un module additionnel se trouve dans les liens.
Il est également possible d’utiliser la combinaison linéaire équivalente en dehors du module RF-/DYNAM Pro. Elle peut être activée dans les paramètres de calcul pour toute combinaison de résultats, pour autant que la règle SRSS soit utilisée. Pour la règle CQC, la procédure est similaire. Cependant, la règle CQC ne peut être utilisée que pour les combinaisons de résultats dans lesquelles seuls des cas de charge de la catégorie Séisme sont utilisés, et où les paramètres de la règle CQC ont été définis dans le cas de charge lui-même.
Quelle règle de combinaison utiliser pour la vérification ? La question reste ouverte. La règle CQC fournit dans tous les cas des résultats plus précis, car elle peut prendre en compte la pertinence des modes propres proches les uns des autres. La règle SRSS peut être utilisée dans les calculs manuels. Dans les calculs assistés par ordinateur, tels que avec RFEM et RF-DYNAM Pro, l’utilisation de la règle CQC, écrite comme une combinaison linéaire, est recommandée, car elle fournit dans tous les cas des résultats corrects et économiques. Le surcoût en terme de puissance de calcul est négligeable.