Fundamentação teórica
Para cada frequência natural, o método do espectro de resposta determina uma resposta modal através do espectro de resposta definido. No caso de sistemas complexos, pode haver um grande número de formas modais a serem consideradas. A sobreposição subsequente revela -se difícil porque, na realidade, todas as vibrações naturais não ocorrem em toda a sua magnitude ao mesmo tempo. Para considerar este facto no cálculo, as respostas modais individuais são sobrepostas de forma quadrática. A norma europeia relativa ao dimensionamento EN 1998-1 fornece duas regras para isso: o método da raiz quadrada da soma dos quadrados (regra SRSS) e o método da combinação quadrática completa (regra CQC) [1].
A aplicação dessas regras geralmente fornece resultados realistas e econômicos, em vez de uma simples adição. No entanto, a direção da excitação e, portanto, os sinais dos resultados são perdidos durante a sobreposição. Consequentemente, os resultados são sempre apresentados como valores máximos na direção positiva e negativa. As forças internas e os momentos correspondentes, por exemplo, um momento correspondente na força axial máxima, são perdidos. Isto deve ser evitado através da modificação da regra SRSS e CQC: As fórmulas serão escritas como uma combinação linear em vez de uma raiz. Esta regra foi introduzida pelo Prof. Dr.-Ing. C. Katz [2] e é apresentado abaixo utilizando a regra SRSS como exemplo.
Comparação de resultados através de um exemplo
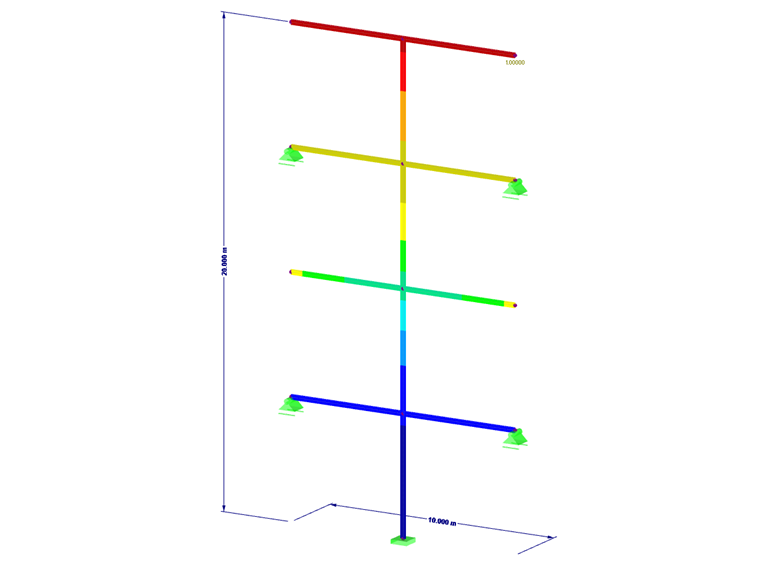
O efeito da combinação linear equivalente é explicado por uma estrutura de aço bidimensional simples. São consideradas três forças internas: força axial N, força de corte Vz e momento My. É utilizado o módulo adicional F-DYNAM Pro-Equivalent Loads. O comportamento no RF -DYNAM Pro - Forced Vibrations é idêntico.
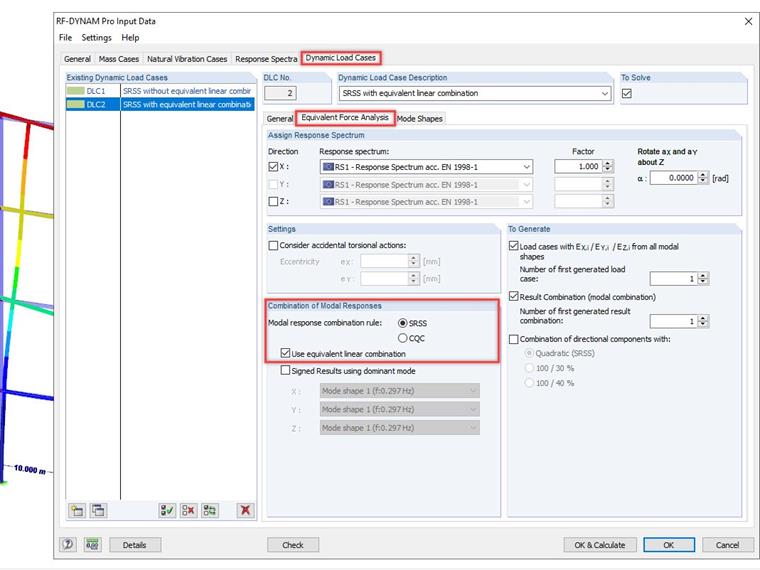
Quatro formas próprias são calculadas exclusivamente na direção X e é utilizado um espectro de resposta baseado na EN 1998-1. A ativação da combinação linear equivalente e a seleção da regra de combinação são efetuadas no separador "Análise de força equivalente" em "Casos de carga dinâmicos" [3].
Os resultados das respostas modais individuais são analisados, por exemplo, no nó número 5 (na barra número 6 → lado esquerdo) e são listados na tabela seguinte.
| Resposta de Forma modal 1 | Resposta de Forma modal 2 | Resposta de Forma modal 3 | Resposta de Forma modal 6 | |
|---|---|---|---|---|
| Força axial N | 1,361 kN | -0,246 kN | 0,815 kN | -2,322 kN |
| Força de corte Vz | 0,480 kN | -1,635 kN | -0,556 kN | 1,546 kN |
| Momento MY | -2,400 kNm | 8,174 kNm | 2,781 kNm | -7,732 kNm |
Os seguintes valores resultam da regra SRSS padrão.
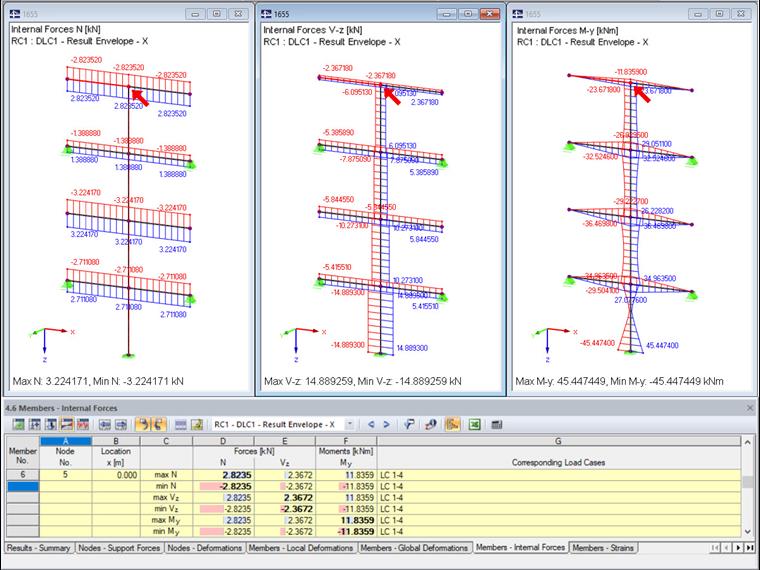
Para avaliar estes resultados no RFEM, é considerada a combinação de resultados gerada. Os resultados máximos são apresentados no gráfico assim como na tabela "4.6 Barras - Forças internas".
Agora, as forças internas são calculadas pela regra SRSS modificada. Devido à combinação linear equivalente, as forças internas e os momentos são calculados separadamente para cada ação máxima. As seguintes forças internas resultam para a força axial máxima.
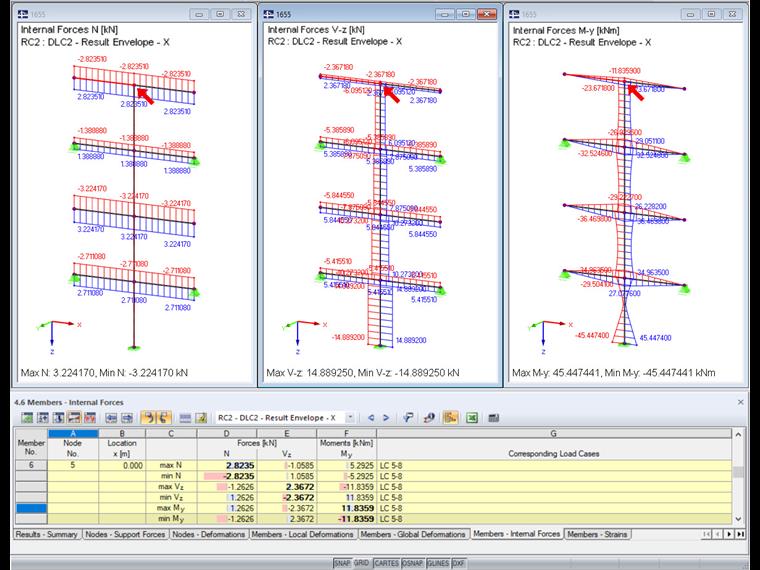
Agora, este procedimento deve ser realizado para todas as ações. As forças internas e os momentos resultantes são apresentados na tabela seguinte.
| Força axial N | Força de corte Vz | Momento MY | |
|---|---|---|---|
| N máx | 2,823 kN | -1,058 kN | 5,292 kNm |
| N mín | -2,823 kN | 1,058 kN | -5,292 kNm |
| Max Vz | -1,263 kN | 2,367 kN | -11,836 kNm |
| Min Vz | 1,263 kN | -2,367 kN | 11,836 kNm |
| Max My | 1,263 kN | -2,367 kN | 11,836 kNm |
| Min My | -1,263 kN | 2,367 kN | -11,836 kNm |
O gráfico no RFEM ainda mostra apenas as forças internas máximas e os momentos. No entanto, as diferenças são visíveis na tabela.
Conclusão e aplicações adicionais
Foi possível mostrar que as forças internas correspondentes são preservadas utilizando a combinação linear equivalente. Se esta regra de combinação é utilizada e importada para os módulos de dimensionamento, geralmente obtém resultados mais económicos. Um exemplo deste uso em um módulo adicional pode ser encontrado nos links.
Também é possível utilizar a combinação linear equivalente fora do módulo adicional RF-/DYNAM Pro. Pode ser ativada nos parâmetros de cálculo para qualquer combinação de resultados, desde que seja utilizada a regra SRSS. O procedimento é semelhante para a regra CQC. No entanto, a regra CQC só pode ser utilizada para aquelas combinações de resultados em que apenas os casos de carga da categoria sísmica foram utilizados e os parâmetros da regra CQC foram definidos no próprio caso de carga.
A questão que permanece sem resposta é: qual regra de combinação deve ser finalmente utilizada para o dimensionamento? Em qualquer caso, a regra CQC fornece resultados mais precisos, uma vez que pode levar em consideração a relevância das formas próprias que se encontram próximas umas das outras. A regra SRSS pode ser utilizada em cálculos manuais. Nos cálculos auxiliados por computador, por exemplo no RFEM e no RF-DYNAM Pro, recomendamos a utilização da regra CQC escrita como uma combinação linear, uma vez que proporciona resultados corretos e económicos em todos os casos. O esforço computacional aumentado é insignificante.
