Нелинейный расчёт деформаций двухпролётной железобетонной балки с учётом ползучести

1. Входные данные

Геометрия

• Статическая система:

Система: Двухпролетная балка
Пролет 1: l₁ = 5.0 м
Пролет 2: l₂ = 4.0 м

• Размеры сечения:

Ширина: b = 1000 мм
Высота: h = 160 мм

• Расчетные свойства:
  • Защитный слой бетона c_nom = 22.0 мм
  • Доступная продольная арматура: Арматура расположена симметрично в сечении сверху и снизу. В верхнем и нижнем слоях имеется по 22 стержня диаметром 6.0 мм (A_s,Seite = 6.22 см²).

Нагрузка

Оба пролета нагружены постоянной нагрузкой, и каждый пролет дополнительно подвержен переменной нагрузке:

• LF1: Случай нагрузки собственный вес: g_k = 1.6 кН/м
• LF2: Случай нагрузки транспортная нагрузка в пролете 1: q_1,k = 5.0 кН/м
• LF3. Случай нагрузки транспортная нагрузка в пролете 2: q_2,k = 5.0 кН/м

Для расчета деформации определяется только квазипостоянная ситуация. Таким образом, возникают следующие три комбинации нагрузок:

• LK1 = LF1 + 0.60 × LF2
• LK2 = LF1 + 0.60 × LF2 + 0.60 × LF2
• LK3 = LF1 + 0.60 × LF3

Материалы

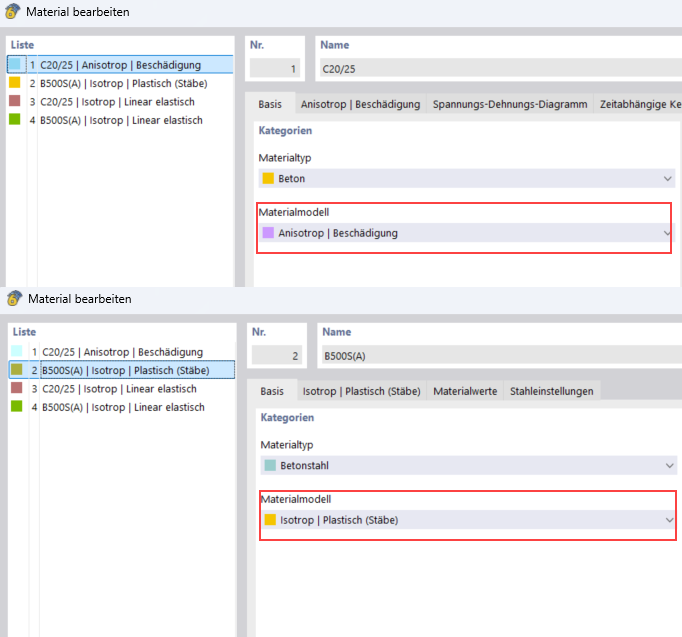
Из библиотеки материалов изначально выбираются бетон класса C20/25 и арматурная сталь класса B500S(A). Для типа материала Бетон нелинейная модель материала Анизотропия | Повреждение хорошо подходит для расчета деформаций. Для типа материала Арматурная сталь следует выбрать подходящую нелинейную материальную модель Изотропия | Пластичность.

• Бетон C20/25

Как только модель материала настроена, отображается конкретная вкладка "Анизотропия | Повреждение":
Определение диаграммы: В рамках этого примера будет проведен расчет деформации, следовательно, можно использовать диаграмму „ГЖК | (Среднее) значение для прогиба“.

Область сжатия:
Для нелинейного анализа область сжатия представляется диаграммой типа „Парабола“ (согласно 3.1.5) и прочностью на сжатие f_cm.

Упрочнение при растяжении::
Для упрочнения при растяжении (Tension Stiffening) используется подход через остаточную прочность бетона на растяжение (Quast | Бетон).

В области растяжения определяется кривая парабола-прямоугольник. До образования трещин кривая следует параболической форме, в которой бетон полностью участвует. Расчетная прочность бетона на растяжение f_ct,R при первичном растрескивании принимается как \( f_{ct,R} = k \cdot f_{ct} = 0.6 \cdot 2,200 = 1,320~\text{N/mm}^2 \) (при расчетной деформации трещины ε_cr,R в 0.1‰). Как только эта расчетная деформация трещины превышается, прочность бетона на растяжение снижается, и кривая напряжение-деформация выравнивается.

Прочность бетона на растяжение f_ct,R не является постоянной величиной, а зависит от деформации определяющего стального волокна в элементе. Она линейно уменьшается, если деформация трещины ε_cr,R превышена и полностью снижается до нуля, как только достигается текучая деформация ε_s арматурной стали.

Эта зависимость между прочностью бетона на растяжение и деформацией стали описывается фактором VMB. Для области ε > ε_cr,R линия напряжение-деформация в области растяжения может быть описана следующим уравнением: \( \sigma_c = VMB \cdot f_{ct,R} \)

До образования трещин (ε_s < ε_cr) определяется коэффициент уменьшения VMB на уровне 1.0, что означает, что бетон сохраняет полное участие в области растяжения, и прочность на растяжение не уменьшается. Уменьшения участия нет, так как бетон еще не треснул. После достижения деформации трещины (ε_cr) бетон начинает терять свое упрочнение при растяжении. Коэффициент уменьшения VMB начинает снижаться. В зависимости от экспонента n_vmb снижение проходит по-разному:
n_vmb = 1.0: Линейное снижение.
n_vmb = 2.0: Более быстрое, крутое снижение.
После достижения предела текучести арматурной стали вся нагрузка на растяжение принимается арматурой, и бетон больше не участвует в ее упрочнении. Коэффициент уменьшения VMB достигает 0.

• Арматурная сталь B500S(A)

Для арматурной стали также можно установить тип диаграммы в конкретной вкладке. В данном примере используется стандартный тип диаграммы.

• Ползучесть и усадка:

Ползучесть сначала активируется в материале бетона на вкладке Временные характеристики бетонного материала. Специфические настройки для ползучести затем хранятся на вкладке Расширенные временные характеристики бетонного материала:

Усадка не анализируется: Из-за почти симметричной арматуры в пролете 1 и лишь небольшой разнице в арматуре в пролете 2 усадочные деформации несущественно влияют на общую деформацию. Усадка поэтому отключена.

Настройки статического анализа

Для нелинейного расчета деформаций используются следующие настройки:

• Тип анализа: Ползучесть представляется линейно через модифицированную кривую напряжение-деформация. Значения деформации бетона умножаются на коэффициент (1 + φ_ef). При этом используется тип "Статический анализ | Ползучесть и усадка (линейная)"
• Модифицирование структуры: Чтобы жесткость арматуры была учтена уже в анализе, необходимо активировать арматурную жесткость через модификацию структуры для железобетона.
• Времена нагрузок на ползучесть: В разделе "Времена" определяется временные параметры нагрузки.

Настройки сетки КЭ

Установлена требуемая длина элементарной ячейки конечных элементов на уровне 100 мм. Кроме того, сетка КЭ сечения для нелинейного анализа обогащена сдвиговым фактором 0,50, так что в сечении создается более детализированная сетка КЭ, что позволяет более точно рассчитывать состояние напряжений.

2. Результаты

Деформация от нелинейного расчета с учетом влияния ползучести в пролете 1 на позиции x=2.20 м составляет 18,2 мм.

Представление основных напряжений σ_x вдоль стержня показывает, что напряжение на растяжение в пролете 1 и в области обработки достигает максимального значения 1.247 Н/мм².

Распределение напряжений в сечении на позиции x=2,20 м иллюстрируется на сечении:

Сравнение с результатами аддона по расчету бетона

Расчет деформации с использованием аддона по расчету бетона на точке x = 2.20 м дает прогиб в 25.6 мм.

Более глубокий анализ расчета в аддоне показывает, что для определения повреждения через коэффициент распределения ζ напряжения из кратковременной нагрузки (без учета ползучести) являются определяющими:

Чтобы учесть влияние кратковременной нагрузки и в нелинейном расчете, можно использовать функцию «Учитывать начальное состояние». Сначала создается комбинация нагрузок, которая не учитывает ползучесть. Эта комбинация затем используется как начальное состояние в основной комбинации нагрузок:

С этими настройками достигается прогиб 22,3 мм.

• Расчет деформации для квазипостоянной ситуации без повреждений на основе соответствующих нагрузок ГЖК-ситуации

Для расчета деформации в квазипостоянной ситуации возможно учитывать определяющее состояние трещин на основе соответствующих комбинаций нагрузок (квазипостоянных ЛК, частых ЛК) (дополнительную информацию можно найти в следующей статье базы знаний).

Это особенно актуально в случае, когда в начале срока службы кратковременная или характерная комбинация нагрузок является определяющей, а в дальнейшем до конца срока службы действует квазипостоянная нагрузка.

Это можно легко настроить в аддоне по расчету бетона, активировав соответственную опцию в конфигурации обслуживания.

В этом примере повреждение от квазипостоянной комбинации нагрузок определяет расчет деформации в характерной комбинации нагрузок. Максимальный прогиб в характерной комбинации нагрузок в аддоне по бетону составляет 30,6 мм:

Опция „Учитывать начальное состояние“ из другой комбинации нагрузок снова используется, чтобы учесть повреждение характерной комбинации нагрузок:

Получается прогиб 25.6 мм:

3. Сравнение результатов

Ситуация нагружения	Нелинейный анализ (NL)	Аддон по расчету бетона	Коэффициент (NL / Add-on)
Учет повреждений от кратковременной нагрузки	22,3	25,6	0,87
Учет повреждений от характерной нагрузки	25,6	30,6	0,84

Разница между нелинейным анализом и подходом из аддона по расчету бетона с использованием заменяющей жесткости объясняется следующим образом: Аддон использует линейно-упругое модель материала и проводит расчет аналитически по всему сечению. Повреждение учитывается глобальным коэффициентом распределения, что делает результаты в целом консервативными. В отличие от этого, нелинейный расчет основан на модели КЭ с нелинейной моделью материала бетона. Повреждение выявляется для каждого элемента сечения индивидуально, и эффекты, такие как упрочнение при растяжении, могут учитываться локально. Это обеспечивает более реалистичное моделирование трещинообразования и распределения напряжений.

4. Заключительные замечания

Нелинейный расчет деформаций двухпролетной железобетонной балки с учетом ползучести четко показывает различия между классическими линейными подходами в аддоне по расчету бетона. Нелинейный анализ позволяет реалистично моделировать распределение напряжений в сечении, особенно в области растяжения после трещинообразования, и локально учитывать влияние упрочнения при растяжении для каждого элемента в сечении. Параллельно аддон по расчету бетона предлагает надежный, простой и особенно удобный подход: он позволяет учитывать эффекты кратковременных нагрузок, а также эффекты длительных нагрузок в характерных (и также частых) ситуациях.