考虑徐变的双跨钢筋混凝土梁的非线性变形分析

1. 输入数据

几何形状

• 结构系统：

系统：双跨梁
跨距 1：l₁ = 5.0 m
跨距 2：l₂ = 4.0 m

• 截面尺寸：

宽度：b = 1000 mm
高度：h = 160 mm

• 设计属性：
  • 混凝土保护层 c_nom = 22.0 mm
  • 现有的纵向钢筋：钢筋在截面上对称排列在上部和下部。在上部和下部各有22根直径为6.0 mm的钢筋（A_s,Seite = 6.22 cm²）。

负载

两个跨间承受永久荷载，且每个跨间额外承受可变荷载：

• LF1: 荷载案例 自重：g_k = 1.6 kN/m
• LF2: 荷载案例 跨间1的交通荷载：q_1,k = 5.0 kN/m
• LF3. 荷载案例 跨间2的交通荷载：q_2,k = 5.0 kN/m

对于变形计算，仅准永久设计情境是决定性的。因此，形成以下三个荷载组合：

• LK1 = LF1 + 0.60 × LF2
• LK2 = LF1 + 0.60 × LF2 + 0.60 × LF2
• LK3 = LF1 + 0.60 × LF3

材料

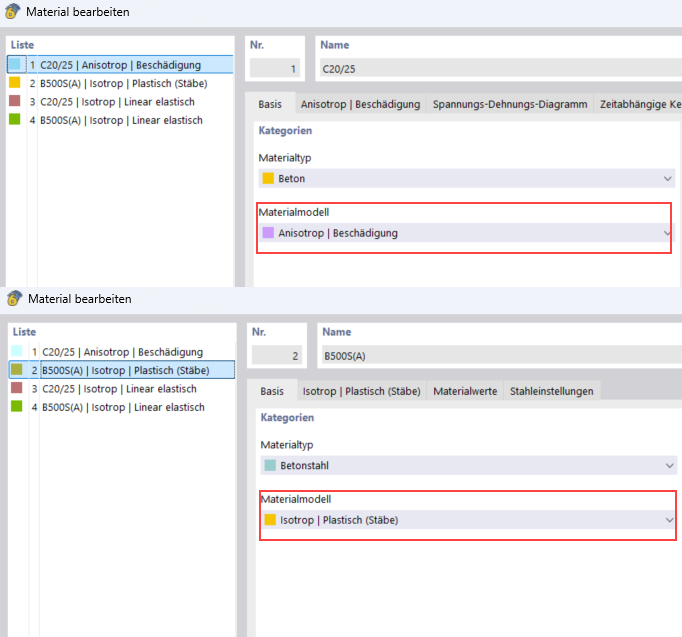
首先从材料库中选取C20/25级混凝土和B500S(A)级钢筋混凝土钢。对于材料类型混凝土，非线性材料模型各向异性 | 损伤非常适合用于变形计算。对于材料类型钢筋混凝土钢，应选择适合的非线性材料模型各向同性 | 塑性。

• 混凝土 C20/25

设置材料模型后，会显示特定的"各向异性 | 损伤"选项卡。
图表定义：在本例中将进行变形计算，因此可以使用“GZG | 整体挠度（中值）”图表。

压缩区：
非线性分析中，压缩区使用“抛物线”图表类型（根据3.1.5）及抗压强度f_cm表现。

拉伸硬化：
对于拉伸硬化（Tension Stiffening），选择基于混凝土剩余拉伸强度（Quast | Beton）的方法。

在拉伸区定义为抛物线-矩形图表曲线。在出现裂缝之前，曲线呈抛物线形，混凝土完全参与的情况下。计算混凝土初裂产生的拉伸强度f_ct,R为 \( f_{ct,R} = k \cdot f_{ct} = 0,6 \cdot 2.200 = 1.320~\text{N/mm}^2 \)（此计算裂缝应变 ε_cr,R 为 0.1‰）。一旦超过此计算裂缝应变，混凝土的拉伸强度降低，拉伸区应力-应变曲线平坦化。

混凝土的拉伸强度f_ct,R不是一个常数，而是依赖于构件中主钢纤维的应变。当超过裂缝应变ε_cr,R时，线性降低，并完全减小为零，当达到钢筋的屈服应变ε_s时。

此混凝土拉伸强度与钢纤维应变的关系由因子VMB描述。对于区间ε > ε_cr,R，拉伸区的应力-应变线可以用以下方程描述：\( \sigma_c = VMB \cdot f_{ct,R} \)。

在裂缝形成之前（ε_s < ε_cr），折减因子VMB保持在1.0，这意味着混凝土在拉伸区的贡献保持完整，拉伸强度没有减小。尚未出现任何折减，因为混凝土还没有开裂。裂缝应变（ε_cr）达到之后，混凝土开始失去其拉伸硬化。折减因子VMB开始减小。根据曲线指数n_vmb，折减进程不同：
n_vmb = 1.0：线性折减。
n_vmb = 2.0：更快、更陡的折减。
达到钢筋混凝土的屈服点后，全部拉力由钢筋承担，混凝土不再提供拉力硬化。折减因子VMB达到0。

• 钢筋混凝土钢 B500S(A)

对于钢筋混凝土钢，也可以在特定注册表中设置图表类型。在此示例中使用标准图表类型。

• 蠕变和收缩：

在混凝土材料的“混凝土的时间依赖特性”选项卡中首先激活蠕变。对蠕变的特定设置随后记录在“混凝土的扩展时间依赖特性”选项卡中。

收缩不做详细研究：由于跨间1的钢筋几乎对称，跨间2仅有微小的钢筋差异，收缩弯曲贡献对整体变形影响微小。因此禁用收缩。

静态分析设置

非线性变形计算使用以下设置：

• 分析类型： 蠕变通过修改的应力-应变曲线线性表现。混凝土的应变值乘以因子(1 + φ_ef)。使用“静态分析 | 蠕变和收缩（线性）”类型。
• 结构修改： 为在分析中考虑到钢筋刚度，钢筋混凝土需通过结构修改激活。
• 蠕变加载时间： 在“时间”部分定义加载时间。

有限元网格设置

有限元元素目标长度设置为100 mm。此外，截面有限元网格非线性分析中附加偏置因子0.50，使截面获得更细的有限元网格，以便更精确计算应力状态。

2. 结果

考虑到蠕变影响的非线性计算中的变形，在跨间1位置x=2.20m处的挠度为18.2 mm。

沿杆件的基本应力σ_x的分布显示出跨间1和支撑区域拉伸应力达到最大值为1.247 N/mm²。

截面在位置x=2,20m的应力分布通过横截面展示：

与混凝土设计附加模块结果比较

使用混凝土设计附加模块计算的变形在位置x = 2.20 m处挠度为25.6 mm。

对附加模块进行更详细的计算显示，损伤的计算通过分布系数ζ的应力主导自短期负载（不包括蠕变影响）：

为了在非线性计算中考虑短期负载的影响，可以使用“考虑初始状态”功能。首先创建一个不考虑蠕变的荷载组合。随后，作为初始状态的荷载组合被引入主要荷载组合中。

使用这些设置，得到挠度为22.3 mm。

• 假定裂缝状态下的永久设计情境的变形计算基于相应荷载的GZG设计情境

在永久设计情境下进行变形计算时，可以考虑来自相应荷载组合的主导裂缝状态（准永久组合，常见组合）（更多信息请参见以下知识库文章）。

例如，当使用期间开始时，短期常见荷载组合或特征荷载组合是主导的，并且在使用结束时是永久荷载影响。

这可以在混凝土设计附加模块中轻松设置，方法是在可用性配置中激活相应选项。

在本示例中，永久荷载组合的损伤对于特征荷载组合的变形计算是决定性因素。混凝土附加模块中特征荷载组合的最大挠度为30.6 mm：

再次使用来自另一个荷载组合的“考虑初始状态”选项来考虑特征荷载组合的损伤：

得到挠度为25.6 mm：

3. 结果比较

荷载情境	非线性分析（NL）	混凝土设计附加模块	比率（NL / Add-on）
考虑来自短期负载的损伤	22.3	25.6	0.87
考虑来自特征影响的损伤	25.6	30.6	0.84

线性分析和混凝土设计附加模块中替代刚度方法之间的差异可以解释为：附加模块使用线性弹性材料并通过整个截面进行计算分析。损伤被全局分配系数考虑，因此结果倾向于保守。相比之下，非线性计算基于具有非线性混凝土模型的有限元模型。损伤在截面每个元素上单独计算，拉伸硬化效应可以局部考虑。因此，裂缝形成和应力分布比线性方法更真实地再现。

4. 结论

考虑蠕变的双跨钢筋混凝土梁的非线性变形计算明显区别于在混凝土设计附加模块中的传统线性方法。非线性分析更真实地再现了截面中的应力分布，尤其是在裂缝后的拉伸区，并且对于截面每个元素局部考虑了拉伸硬化影响。与此同时，混凝土设计附加模块提供一种可靠、简单且非常舒适的方法：它允许在特征（及常见）设计情境中，同时考虑短期负载和长期负载的效应。