Nichtlineare Verformungsanalyse eines zweifeldrigen Stahlbetonträgers unter Berücksichtigung von Kriechen

1. Eingabedaten

Geometrie

• Das Statische System:

System: Zweifeldträger
Spannweite Feld 1: l₁ = 5.0 m
Spannweite Feld 2: l₂ = 4.0 m

• Querschnittsabmessung:

Breite: b = 1000 mm
Höhe: h = 160 mm

• Bemessungseigenschaften:
  • Betondeckung c_nom = 22.0 mm
  • Vorhandene Längsbewehrung: Die Bewehrung ist im Querschnitt symmetrisch oben und unten angeordnet. In der oberen und unteren Lage sind jeweils 22 Stäbe mit einem Durchmesser von 6.0 mm vorhanden (A_s,Seite = 6.22 cm²).

Belastung

Die beiden Felder sind mit einer ständigen Last belastet, und jedes Feld ist zusätzlich mit einer veränderlichen Last beansprucht:

• LF1: Lastfall Eigengewicht: g_k = 1.6 kN/m
• LF2: Lastfall Verkehrslast in Feld 1: q_1,k = 5.0 kN/m
• LF3. Lastfall Verkehrslast in Feld 2: q_2,k = 5.0 kN/m

Für die Verformungsberechnung ist nur die quasi-ständige Bemessungssituation maßgebend. Daraus ergeben sich die folgenden drei Lastkombinationen:

• LK1 = LF1 + 0.60 × LF2
• LK2 = LF1 + 0.60 × LF2 + 0.60 × LF2
• LK3 = LF1 + 0.60 × LF3

Materialien

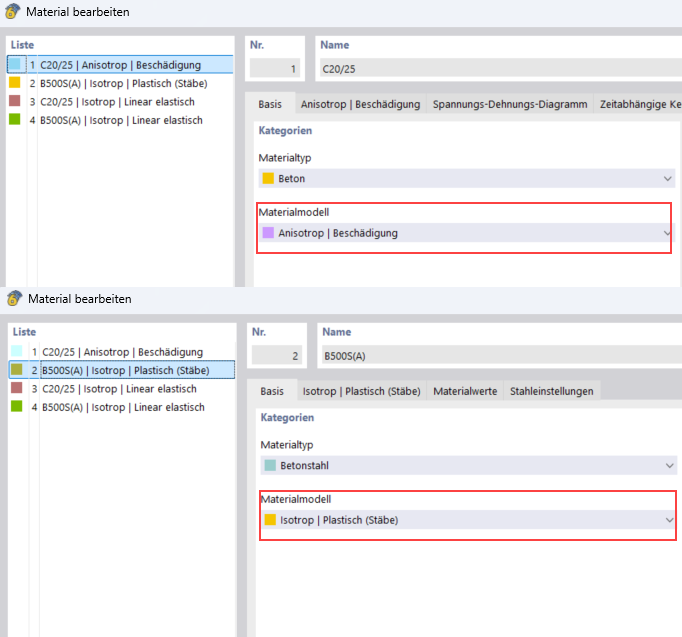
Aus der Materialbibliothek werden zunächst Beton der Klasse C20/25 und Betonstahl der Klasse B500S(A) übernommen. Für den Materialtyp Beton ist das nichtlineare Materialmodell Anisotrop | Beschädigung für die Verformungsberechnung gut geeignet. Für den Materialtyp Betonstahl sollte das geeignete nichtlineare Materialmodell Isotrop | Plastisch ausgewählt werden.

• Beton C20/25

Sobald das Materialmodell eingestellt ist, zeigt sich das spezifischen Register "Anisotrop | Beschädigung":
Diagrammdefinition: Im Rahmen dieses Beispiels soll eine Verformungsberechnung durchgeführt werden, daher kann das Diagramm „GZG | (Mittel-)Werte für Durchbiegung“ verwendet werden.

Druckbereich:
Für die nichtlineare Analyse wird der Druckbereich mit dem Diagrammtyp „Parabel“ (nach 3.1.5) sowie der Druckfestigkeit f_cm abgebildet.

Zugversteifung:
Für die Zugversteifung (Tension Stiffening) wird der Ansatz über die Beton-Restzugfestigkeit (Quast | Beton) gewählt.

Im Zugbereich wird eine Parabel-Rechteck-Diagramm-Kurve definiert. Vor der Rissbildung folgt die Kurve einer parabolischen Form, in der der Beton voll mitwirkt. Die rechnerische Zugfestigkeit des Betons f_ct,R bei Erstrissbildung wird als \( f_{ct,R} = k \cdot f_{ct} = 0,6 \cdot 2.200 = 1.320~\text{N/mm}^2 \) angenommen (bei einer rechnerischen Rissdehnung ε_cr,R von 0.1‰). Sobald diese rechnerische Rissdehnung überschritten wird, nimmt die Betonzugfestigkeit ab, und die Spannungs-Dehnungs-Kurve verflacht sich.

Die Zugfestigkeit des Betons f_ct,R ist keine konstante Größe, sondern hängt von der Dehnung der maßgebenden Stahlfaser im Bauteil ab. Sie nimmt linear ab, wenn die Rissdehnung ε_cr,R überschritten wird und verringert sich vollständig auf null, sobald die Fließdehnung ε_s des Bewehrungsstahls erreicht wird.

Diese Abhängigkeit zwischen der Betonzugfestigkeit und der Stahldehnung wird durch den Faktor VMB beschrieben. Für den Bereich ε > ε_cr,R kann die Spannungs-Dehnungs-Linie im Zugbereich mit folgender Gleichung beschrieben werden: \( \sigma_c = VMB \cdot f_{ct,R} \)

Vor der Rissbildung (ε_s < ε_cr) bleibt der Abminderungsfaktor VMB bei 1,0, was bedeutet, dass der Beton seine volle Mitwirkung im Zugbereich behält und die Zugfestigkeit nicht reduziert wird. Es gibt noch keine Abminderung der Mitwirkung, da der Beton noch nicht gerissen ist. Nach Erreichen der Rissdehnung (ε_cr) beginnt der Beton, seine Zugversteifung zu verlieren. Der Abminderungsfaktor VMB nimmt ab. Je nach Verlaufsexponent n_vmb verläuft die Reduktion unterschiedlich:
n_vmb = 1,0: Lineare Reduktion.
n_vmb = 2,0: Schnellere, steilere Reduktion.
Nach Erreichen der Fließgrenze des Bewehrungsstahls übernimmt die Bewehrung die gesamte Zugspannung, und der Beton trägt nicht mehr zur Zugversteifung bei. Der Abminderungsfaktor VMB erreicht 0.

• Betonstahl B500S(A)

Für den Betonstahl lässt sich ebenfalls in dem spezifischen Register der Diagrammtyp einstellen. In diesem Beispiel wird das Diagrammtyp Standard verwendet.

• Kriechen und Schwinden:

Das Kriechen wird zunächst im Betonmaterial im Register Zeitabhängige Kennwerte des Betons aktiviert. Die spezifischen Einstellungen für das Kriechen sind anschließend im Register Erweiterte zeitabhängige Kennwerte des Betons hinterlegt:

Das Schwinden wird nicht näher untersucht: Wegen der nahezu symmetrischen Bewehrung im Feld 1 und der nur kleinen Bewehrungsdifferenz im Feld 2 tragen die Schwindkrümmungen nur unwesentlichen zur Gesamtverformung bei. Schwinden ist daher deaktiviert.

Statische Analyse Einstellungen

Für die nichtlineare Verformungsberechnung werden die folgenden Einstellungen verwendet:

• Analyse Typ: Das Kriechen wird linear über eine modifizierte Spannungs-Dehnungs-Linie abgebildet. Die Dehnungswerte des Betons werden mit dem Faktor (1 + φ_ef) multipliziert. Dabei ist der Analyse-Typ „Statische Analyse | Kriechen und Schwinden (linear)“ zu verwenden
• Strukturmodifikation: Damit die Bewehrungssteifigkeit bereits in der Analyse berücksichtigt wird, muss die Stabbewehrung über eine Strukturmodifikation für Stahlbeton aktiviert werden.
• Kriechbelastungszeiten: Im Abschnitt "Zeiten" erfolgt die Definition der Belastungszeiten.

FE-Netz Einstellungen

Die angestrebte Elementlänge der finiten Elemente wurde auf 100 mm eingestellt. Zusätzlich ist das Querschnitts-FE-Netz für die nichtlineare Analyse mit einem Versatzfaktor von 0,50 versehen, sodass im Querschnitt ein feineres FE-Netz entsteht, das eine genauere Berechnung des Spannungszustands ermöglicht.

2. Ergebnisse

Die Verformung aus der nichtlinearen Berechnung unter Berücksichtigung des Kriecheinflusses ergibt im Feld 1 an der Position x=2.20m eine Durchbiegung von 18.2 mm.

Die Darstellung der Grundspannungen σ_x entlang des Stabes verdeutlicht, dass die Zugspannung in Feld 1 und im Stützenbereich einen Maximalwert von 1.247 N/mm² erreicht.

Die Spannungsverteilung im Querschnitt an der Position x=2,20m wird durch einen Schnitt veranschaulicht:

Vergleich mit den Ergebnissen des Betonbemessung-Addons

Eine Berechnung der Verformung mit dem Betonbemessungs-Add-on ergibt an der Stelle x = 2.20 m eine Durchbiegung von 25.6 mm.

Eine genauere Betrachtung der Berechnung im Add-on zeigt, dass für die Ermittlung der Schädigung über den Verteilungsbeiwert ζ die Spannungen aus der Kurzzeitbelastung (ohne Einfluss von Kriechen) maßgebend sind:

Um die Auswirkungen der Kurzzeitbelastung auch in der nichtlinearen Berechnung zu berücksichtigen, kann die Funktion „Anfangszustand berücksichtigen“ verwendet werden. Zunächst wird eine Lastkombination, die kein Kriechen berücksichtigt, erstellt. Diese Lastkombination wird dann als Anfangszustand in die Hauptlastkombination übernommen:

Mit diesen Einstellungen wird eine Durchbiegung von 22,3 mm erreicht.

• Verformungsberechnung für die quasi-ständige Bemessungssituation mit Risszustand basierend auf den zugehörigen Lasten der GZG-Bemessungssituation

Für die Berechnung der Verformung in der quasi-ständigen Bemessungssituation ist es möglich, den maßgebenden Risszustand aus den zugehörigen Lastkombinationen (Quasi-ständige LK, Häufige LK) zu berücksichtigen (weitere Informationen finden Sie im folgenden Knowledge-Base-Artikel).

Dies ist beispielsweise der Fall, wenn zu Beginn der Nutzungsdauer kurzfristig die häufige oder charakteristische Lastkombination maßgebend ist und im weiteren Verlauf bis zum Ende der Nutzungsdauer die quasi-ständige Einwirkung wirkt.

Diese lässt sich im Betonbemessungs-Add-on einfach einstellen, indem die entsprechende Option in der Gebrauchstauglichkeitskonfiguration aktiviert wird.

In diesem Beispiel ist die Schädigung aus der Quasi-ständigen Lastkombination maßgebend für die Berechnung der Verformung in der charakteristischen Lastkombination. Die maximale Durchbiegung der charakteristischen Lastkombination im Beton-Add-on beträgt 30,6 mm:

Die Option ‚Anfangszustand berücksichtigen‘ aus einer anderen Lastkombination wird wieder verwendet, um die Schädigung der charakteristischen Lastkombination zu berücksichtigen:

Es ergibt sich eine Durchbiegung von 25.6 mm:

3. Vergleich der Ergebnisse

Lastsituation	Nichtlineare Analyse (NL)	Betonbemessungs-Add-on	Ratio (NL / Add-on)
Berücksichtigung von Schädigung aus Kurzzeitbelastung	22,3	25,6	0,87
Berücksichtigung der Schädigung aus charakteristischer Einwirkung	25,6	30,6	0,84

Der Unterschied zwischen der nichtlinearen Analyse und dem Ansatz von Ersatzsteifigkeiten im Betonbemessungs-Addon lässt sich folgendermaßen erklären: Das Addon verwendet ein linear-elastisches Material und führt die Berechnung analytisch über den gesamten Querschnitt durch. Die Schädigung wird dabei durch einen globalen Verteilungsbeiwert berücksichtigt, wodurch die Ergebnisse tendenziell konservativ ausfallen. Im Gegensatz dazu basiert die nichtlineare Berechnung auf einem FE-Modell mit einem nichtlinearen Betonmaterialmodell. Die Schädigung wird hier für jedes Element des Querschnitts individuell ermittelt, und Effekte wie Tension Stiffening können lokal berücksichtigt werden. Dadurch wird die Rissbildung und Spannungsverteilung deutlich realitätsnäher abgebildet.

4. Schlussbemerkungen

Die nichtlineare Verformungsberechnung eines zweifeldrigen Stahlbetonträgers unter Berücksichtigung von Kriechen zeigt deutlich die Unterschiede zu klassischen linearen Ansätzen im Betonbemessungs-Addon. Die nicht-lineare Analyse ermöglicht eine realitätsnahe Abbildung der Spannungsverteilung im Querschnitt, insbesondere im Zugbereich nach Rissbildung, und berücksichtigt den Einfluss von Tension Stiffening lokal für jedes Element im Querschnitt. Parallel zeigt das Betonbemessungs-Add-on einen zuverlässigen, einfachen und besonders komfortablen Ansatz: Es ermöglicht, Effekte aus Kurzzeitbelastungen sowie Effekte von Dauerlasten in die charakteristischen (und auch häufigen) Bemessungssituationen zu berücksichtigen.