Nieliniczna analiza odkształceń dwupolowej belki żelbetowej z uwzględnieniem pełzania

1. Dane wejściowe

Geometria

• Układ statyczny:

System: belka przęsłowa dwuprzęsłowa
Rozpiętość przęsła 1: l₁ = 5,0 m
Rozpiętość przęsła 2: l₂ = 4,0 m

• Wymiary przekroju:

Szerokość: b = 1000 mm
Wysokość: h = 160 mm

• Właściwości projektowe:
  • Otulina nominalna betonu c_nom = 22,0 mm
  • Istniejące zbrojenie podłużne: Zbrojenie rozmieszczone symetrycznie w górnej i dolnej części przekroju. W górnej i dolnej warstwie znajduje się po 22 pręty o średnicy 6,0 mm (A_s,bok = 6,22 cm²).

Obciążenie

Oba przęsła są obciążone stałym obciążeniem, a każde przęsło jest dodatkowo obciążone obciążeniem zmiennym:

• LF1: Obciążenie własne: g_k = 1,6 kN/m
• LF2: Obciążenie użytkowe w przęśle 1: q_1,k = 5,0 kN/m
• LF3. Obciążenie użytkowe w przęśle 2: q_2,k = 5,0 kN/m

Do obliczeń przemieszczeń istotna jest jedynie quasi-stała sytuacja projektowa. Stąd wyprowadzone są następujące trzy kombinacje obciążeń:

• LK1 = LF1 + 0,60 × LF2
• LK2 = LF1 + 0,60 × LF2 + 0,60 × LF2
• LK3 = LF1 + 0,60 × LF3

Materiały

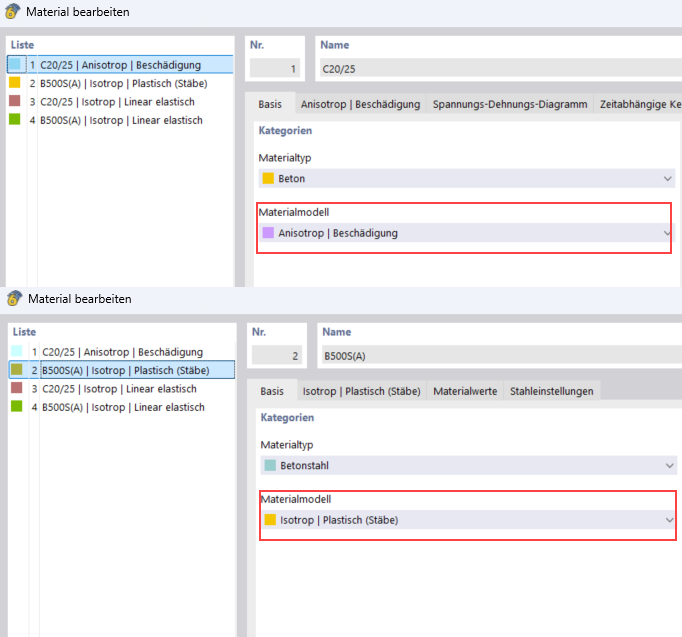
Z biblioteki materiałów przejmowane są najpierw beton klasy C20/25 i stal zbrojeniowa klasy B500S(A). Dla typu materiału Beton odpowiedni do obliczeń przemieszczeń jest nieliniowy model materiałowy Anizotropowy | Uszkodzenie. Dla typu materiału Stal zbrojeniowa należy wybrać odpowiedni nieliniowy model materiałowy Izotropowy | Plastyczny.

• Beton C20/25

Po ustawieniu modelu materiałowego ukazuje się specyficzna zakładka "Anizotropowy | Uszkodzenie":
Definicja wykresu: W ramach niniejszego przykładu zostanie przeprowadzone obliczenie przemieszczenia, dlatego można użyć wykresu „GZG | Wartości średnie na ugięcia”.

Obszar ściskania:
Dla nieliniowej analizy obszar ściskania odwzorowano typem wykresu „Parabola” (zgodnie z 3.1.5) oraz wytrzymałością na ściskanie f_cm.

Usztywnienie na rozciąganie:
Dla usztywnienia na rozciąganie (Tension Stiffening) wybrano podejście z wykorzystaniem resztkowej wytrzymałości betonu na rozciąganie (Quast | Beton).

W obszarze rozciągania definiuje się parabolę-prostokąt wykresu. Przed pojawieniem się pęknięć krzywa przyjmuje postać paraboliczną, gdzie beton działa w pełni. Przyjmuje się, że teoretyczna wytrzymałość betonu na rozciąganie f_ct,R przy pierwszych pęknięciach wynosi \( f_{ct,R} = k \cdot f_{ct} = 0,6 \cdot 2.200 = 1.320~\text{N/mm}^2 \) (przy założonym odkształceniu pęknięcia ε_cr,R wynoszącym 0,1‰). Po przekroczeniu tego teoretycznego odkształcenia pęknięcia wytrzymałość betonu na rozciąganie maleje, a krzywa naprężenie-odkształcenie się spłaszcza.

Wytrzymałość betonu na rozciąganie f_ct,R nie jest wielkością stałą, lecz zależy od odkształcenia włókna stali w elemencie. Maleje liniowo po przekroczeniu odkształcenia pęknięcia ε_cr,R i całkowicie zmniejsza się do zera po osiągnięciu odkształcenia plastycznego ε_s stali zbrojeniowej.

Ta zależność między wytrzymałością betonu na rozciąganie a odkształceniem stali jest opisana współczynnikiem VMB. Dla obszaru ε > ε_cr,R linię naprężenie-odkształcenie w obszarze rozciągania można opisać równaniem: \( \sigma_c = VMB \cdot f_{ct,R} \)

Przed pęknięciem (ε_s < ε_cr) współczynnik redukcji VMB wynosi 1,0, co oznacza, że beton zachowuje swoją pełną rolę w obszarze rozciągania i wytrzymałość na rozciąganie nie jest zredukowana. Nie występuje jeszcze redukcja udziału, ponieważ beton nie ma jeszcze pęknięć. Po osiągnięciu odkształcenia pęknięcia (ε_cr) beton zaczyna tracić swoje usztywnienie na rozciąganie. Współczynnik redukcji VMB maleje. W zależności od wykładnika przebiegu n_vmb redukcja przebiega różnie:
n_vmb = 1,0: Redukcja liniowa.
n_vmb = 2,0: Szybsza, bardziej stroma redukcja.
Po osiągnięciu granicy plastyczności stali zbrojeniowej, zbrojenie przejmuje całkowite naprężenia rozciągające, a beton nie przyczynia się już do usztywniania na rozciąganie. Współczynnik redukcji VMB osiąga 0.

• Stal zbrojeniowa B500S(A)

Dla stali zbrojeniowej również można ustawić typ wykresu w specyficznej zakładce. W tym przykładzie używany jest standardowy typ wykresu.

• Pełzanie i skurcz:

Pełzanie jest na początku aktywowane w materiale betonowym w zakładce Cechy zależne od czasu. Specyficzne ustawienia dla pełzania są następnie zapisane w zakładce Zaawansowane właściwości czasowe betonu:

Skurcz nie jest szczegółowo badany: Z powodu prawie symetrycznego zbrojenia w polu 1 i jedynie małej różnicy w zbrojeniu w polu 2, krzywizny skurczowe przyczyniają się nieznacznie do całkowitego przemieszczenia. Skurcz jest więc wyłączony.

Ustawienia analizy statycznej

Do nieliniowego obliczenia przemieszczeń używane są następujące ustawienia:

• Typ analizy: Pełzanie jest odwzorowane liniowo przez zmodyfikowaną linię naprężenie-odkształcenie. Wartości odkształceń betonu są mnożone przez współczynnik (1 + φ_ef). Używany jest typ analizy „Analiza statyczna | Pełzanie i skurcz (liniowo)”
• Modyfikacja struktury: Aby uwzględnić sztywność zbrojenia już w analizie, należy aktywować zbrojenie prętów przez modyfikację struktury dla betonu zbrojonego.
• Czasy obciążenia pełzaniem: W sekcji "Czas" definiowane są czasy obciążenia.

Ustawienia siatki FE

Długość elementów skończonych została ustawiona na 100 mm. Ponadto siatka FE przekroju dla analizy nieliniowej jest wyposażona w współczynnik przesunięcia wynoszący 0,50, co powoduje powstanie dokładniejszej siatki FE w przekroju, umożliwiającej dokładniejsze obliczenie stanu naprężenia.

2. Wyniki

Przemieszczenie z nieliniowego obliczenia z uwzględnieniem wpływu pełzania daje w polu 1 w pozycji x=2,20m ugięcie 18,2 mm.

Reprezentacja naprężeń podstawowych σ_x wzdłuż pręta uwidacznia, że naprężenie rozciągające w polu 1 i w obszarze podporowym osiąga maksymalną wartość 1,247 N/mm².

Rozkład naprężeń w przekroju w pozycji x=2,20m ilustruje przekrój:

Porównanie z wynikami dodatku do wymiarowania betonu

Obliczenie przemieszczenia za pomocą dodatku do wymiarowania betonu daje w miejscu x = 2,20 m ugięcie 25,6 mm.

Dokładniejsze zbadanie obliczeń w dodatku pokazuje, że do określenia uszkodzenia przez współczynnik rozkładu ζ istotne są naprężenia z krótkotrwałego obciążenia (bez wpływu pełzania):

Aby także uwzględnić skutki krótkotrwałego obciążenia w obliczeniu nieliniowym, można użyć funkcji „Uwzględnij stan początkowy”. Najpierw tworzona jest kombinacja obciążeń, która nie uwzględnia pełzania. Ta kombinacja obciążeń jest następnie przejmowana jako stan początkowy do głównej kombinacji obciążeń:

Z tymi ustawieniami osiągane jest ugięcie 22,3 mm.

• Obliczenie przemieszczenia dla quasi-stałej sytuacji projektowej wraz z rysującym się stanem na podstawie przypisanych obciążeń sytuacji projektowej GZG

Dla obliczenia przemieszczenia w quasi-stałej sytuacji projektowej można uwzględnić istotny stan rysowania wynikający z przypisanych kombinacji obciążeń (quasi-stałe LK, często występujące LK) (więcej informacji można znaleźć w poniższym artykule bazy wiedzy).

Tak jest na przykład, gdy na początku okresu użytkowania tymczasowo istotna jest kombinacja obciążeń często występująca lub charakterystyczna i w dalszym przebiegu aż do końca okresu użytkowania działa quasi-stały wpływ.

Można to łatwo ustawić w dodatku do wymiarowania betonu przez aktywację odpowiedniej opcji w konfiguracji użytkowania.

W tym przykładzie, uszkodzenie z quasi-stałej kombinacji obciążeń jest istotne dla obliczenia przemieszczenia w charakterystycznej kombinacji obciążeń. Maksymalne ugięcie charakterystycznej kombinacji obciążeń w dodatku betonowym wynosi 30,6 mm:

Opcja ‚Uwzględnij stan początkowy’ z innej kombinacji obciążeń jest ponownie używana, aby uwzględnić uszkodzenie charakterystycznej kombinacji obciążeń:

Osiąga się ugięcie 25,6 mm:

3. Porównanie wyników

Sytuacja obciążeniowa	Analiza nieliniowa (NL)	Dodatek do wymiarowania betonu	Współczynnik (NL / Dodatek)
Uwzględnienie uszkodzenia z krótkotrwałego obciążenia	22,3	25,6	0,87
Uwzględnienie uszkodzenia z charakterystycznego oddziaływania	25,6	30,6	0,84

Różnica między analizą nieliniową a podejściem z zastępczymi sztywnościami w dodatku do wymiarowania betonu można wyjaśnić następująco: Dodatek używa materiału liniowego-elastycznego i przeprowadza obliczenia analitycznie przez cały przekrój. Uszkodzenie jest uwzględniane za pomocą globalnego współczynnika rozkładu, co powoduje, że wyniki są tendencjonalnie konserwatywne. Z kolei obliczenia nieliniowe opierają się na modelu FE z nieliniowym modelem materiałowym dla betonu. Uszkodzenie jest tutaj określane indywidualnie dla każdego elementu przekroju, a efekty takie jak usztywnienie na rozciąganie mogą być lokalizowane. Dzięki temu pękanie i rozkład naprężeń są przedstawiane znacznie bardziej realistycznie.

4. Uwagi końcowe

Nieliniowe obliczenia przemieszczeń dwuprzęsłowej belki żelbetowej z uwzględnieniem pełzania wyraźnie pokazują różnice w stosunku do klasycznych liniowych podejść w dodatku do wymiarowania betonu. Analiza nieliniowa umożliwia realistyczne odwzorowanie rozkładu naprężeń w przekroju, w szczególności w obszarze rozciągania po pęknięciu, oraz uwzględnia wpływ usztywnienia na rozciąganie lokalnie dla każdego elementu w przekroju. Równocześnie dodatek do wymiarowania betonu oferuje niezawodne, proste i bardzo wygodne podejście: Umożliwia uwzględnienie efektów krótkotrwałych obciążeń oraz efektów długotrwałych obciążeń w charakterystycznych (a także często występujących) sytuacjach projektowych.