Nelineární analýza deformací železobetonového nosníku o dvou polích při zohlednění dotvarování

1. Vstupní data

Geometrie

• Statický systém:

Systém: Dvoupolový nosník Rozpětí pole 1: l₁ = 5,0 m Rozpětí pole 2: l₂ = 4,0 m

• Rozměry průřezu:

Šířka: b = 1000 mm Výška: h = 160 mm

• Vlastnosti pro návrh:
  • Krytí betonu c_nom = 22,0 mm
  • Stávající podélná výztuž: Výztuž je v průřezu symetricky umístěna nahoře a dole. V horní a dolní vrstvě je umístěno 22 tyčí s průměrem 6,0 mm (A_s,Strana = 6,22 cm²).

Zatížení

Obě pole jsou zatížena stálým zatížením a každé pole je navíc zatíženo proměnlivým zatížením:

• LF1: Zatěžovací stav vlastní tíha: g_k = 1,6 kN/m
• LF2: Zatěžovací stav dopravní zatížení v poli 1: q_1,k = 5,0 kN/m
• LF3. Zatěžovací stav dopravní zatížení v poli 2: q_2,k = 5,0 kN/m

Pro výpočet deformace je rozhodující pouze kvazistálá návrhová situace. Z toho plynou následující tři kombinace zatížení:

• LK1 = LF1 + 0,60 × LF2
• LK2 = LF1 + 0,60 × LF2 + 0,60 × LF2
• LK3 = LF1 + 0,60 × LF3

Materiály

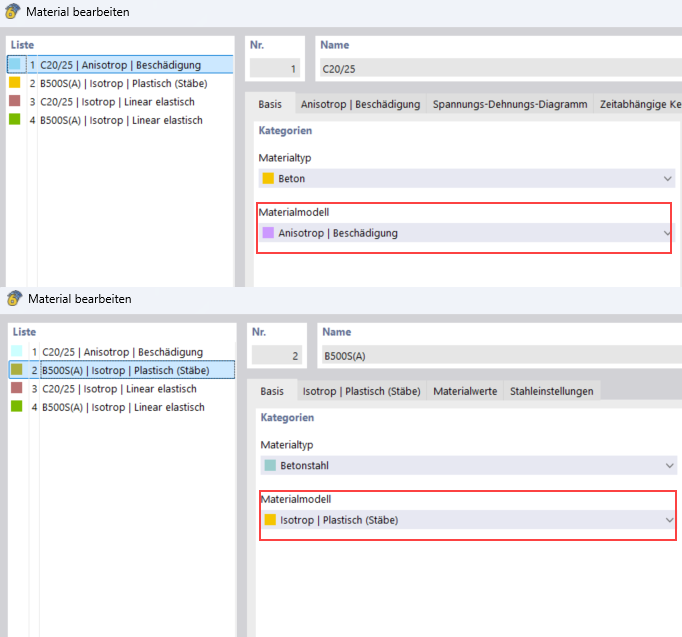
Z knihovny materiálů se nejprve převezme beton třídy C20/25 a ocelová výztuž třídy B500S(A). Pro typ materiálu beton je pro výpočet deformace vhodný nelineární materiálový model Anizotropní | Poškození. Pro typ materiálu ocelová výztuž by měl být vybrán vhodný nelineární materiálový model Izotropní | Plastický.

• Beton C20/25

Jakmile je nastaven materiálový model, objeví se specifická záložka "Anizotropní | Poškození": Definice diagramu: V rámci tohoto příkladu má být proveden výpočet deformace, proto lze použít diagram „GZG | (střední) hodnoty pro průhyb“.

Tlková oblast: Pro nelineární analýzu je tlková oblast reprezentována typem diagramu „Parabola“ (podle 3.1.5) a tlakovou pevností f_cm.

Zpevňování při tahání: Pro zpevňování při tahání (Tension Stiffening) se volí přístup přes zbytkovou pevnost betonu v tahu (Quast | Beton).

V tahové oblasti je definována parabolicko-obdélníková křivka diagramu. Před vznikem trhlin sleduje křivka parabolickou formu, v níž je beton plně účinný. Výpočtová pevnost betonu v tahu f_ct,R při vzniku první trhliny je přijata jako \( f_{ct,R} = k \cdot f_{ct} = 0,6 \cdot 2 200 = 1 320~\text{N/mm}^2 \) (při výpočtovém prodloužení trhliny ε_cr,R 0,1‰). Jakmile je toto výpočtové prodloužení trhliny překročeno, pevnost betonu v tahu klesá a napěťově-deformační křivka se zplošťuje.

Pevnost betonu v tahu f_ct,R není konstantní veličina, ale závisí na prodloužení určující ocelové vlákna v prvku. Lineárně klesá, když je překročeno prodloužení trhliny ε_cr,R a zcela klesá na nulu, jakmile je dosaženo mezního prodloužení ε_s výztuže.

Tato závislost mezi pevností betonu v tahu a prodloužením oceli je popsána faktorem VMB. V oblasti ε > ε_cr,R lze napěťově-deformační křivku v tahové oblasti popsat následující rovnicí: \( \sigma_c = VMB \cdot f_{ct,R} \)

Před vznikem trhlin (ε_s < ε_cr) zůstává redukční faktor VMB na hodnotě 1,0, což znamená, že beton si v tahové oblasti stále uchovává svou plnou účinnost a pevnost v tahu není redukována. Nedochází k žádné redukci účinnosti, protože beton ještě není prasklý. Po dosažení prodloužení trhliny (ε_cr) začíná beton ztrácet své zpevňování při tahání. Redukční faktor VMB klesá. V závislosti na průběhovém exponentu n_vmb probíhá redukce odlišně: n_vmb = 1,0: Lineární redukce. n_vmb = 2,0: Rychlejší, strmější redukce. Po dosažení mezního prodloužení výztužné oceli převezme výztuž celkové tahové napětí a beton již k zpevnění při tahání nepřispívá. Redukční faktor VMB dosáhne hodnoty 0.

• Ocelová výztuž B500S(A)

Pro ocelovou výztuž lze také nastavit typ diagramu ve specifické záložce. V tomto příkladu je použit typ diagramu Standard.

• Únosnost a smršťování:

Únosnost je zpočátku aktivována v betonu v záložce Časově závislé charakteristiky betonu. Specifická nastavení pro únosnost jsou následně uložena v záložce Rozšířené časově závislé charakteristiky betonu:

Smršťování není detailně zkoumáno: Vzhledem k téměř symetrické výztuži v poli 1 a pouze malé rozdílné výztuži v poli 2 přispívají smršťovací zakřivení jen nevýznamně k celkové deformaci. Smršťování je proto deaktivováno.

Nastavení statické analýzy

Pro nelineární výpočet deformace jsou použita následující nastavení:

• Typ analýzy: Únosnost je lineárně reprezentována modifikovanou napěťově-deformační křivkou. Deformační hodnoty betonu jsou násobeny faktorem (1 + φ_ef). Je použit typ analýzy „Statická analýza | Únosnost a smršťování (lineární)“.
• Modifikace struktury: Aby byla tuhost výztuže zahrnuta již v analýze, musí být tyčová výztuž aktivována prostřednictvím modifikace struktury pro železobeton.
• Časy zatěžování pro únosnost: V oddíle "Časy" se definuje doba zatěžování.

Nastavení sítě konečných prvků

Požadovaná délka prvků sítě konečných prvků byla nastavena na 100 mm. Navíc je síť konečných prvků průřezu pro nelineární analýzu opatřena posuvným faktorem 0,50, takže v průřezu vzniká jemnější síť konečných prvků, což umožňuje přesnější výpočet napěťových stavů.

2. Výsledky

Deformace z nelineárního výpočtu s ohledem na vliv únosnosti v poli 1 na pozici x=2,20 m představuje průhyb 18,2 mm.

Zobrazení základních napětí σ_x podél tyče objasňuje, že tahové napětí v poli 1 a v oblasti podpory dosahuje maximální hodnoty 1 247 N/mm². Rozložení napětí v průřezu na pozici x=2,20 m je ilustrováno průřezem:

Porovnání s výsledky přídavného modulu pro návrh betonu

Výpočet deformace s přídavným modulem pro návrh betonu dává na místě x = 2,20 m průhyb 25,6 mm.

Podrobnější pohled na výpočet v přídavném modulu ukazuje, že pro určení poškození pomocí rozdělovacího koeficientu ζ jsou rozhodující napětí z krátkodobého zatížení (bez vlivu únosnosti):

Chcete-li zohlednit účinky krátkodobého zatížení i v nelineárním výpočtu, lze použít funkci „Zohlednit počáteční stav“. Nejprve se vytvoří kombinace zatížení, která nezahrnuje únosnost. Tato kombinace zatížení se pak přenese jako počáteční stav do hlavní kombinace zatížení:

Tímto nastavením se dosáhne průhybu 22,3 mm.

• Výpočet deformace pro kvazistálou návrhovou situaci s trhlinovým stavem na základě příslušných zatížení návrhové situace GZG

Pro výpočet deformace v kvazistálé návrhové situaci je možné zohlednit rozhodující stav trhlin z příslušných kombinací zatížení (Kvazistálé LK, Časté LK) (další informace naleznete v následujícím článku znalostní databáze).

To je například případ, kdy na začátku životnosti je rozhodující krátkodobě častá nebo charakteristická kombinace zatížení a v dalším průběhu až do konce životnosti působí kvazistálé zatížení.

To lze jednoduše nastavit v přídavném modulu pro návrh betonu, a to aktivací příslušné volby v konfiguraci použitelnosti.

V tomto příkladu je pro výpočet deformace v charakteristické kombinaci zatížení rozhodující poškození z kvazistálé kombinace zatížení. Maximální průhyb charakteristické kombinace zatížení v přídavném modulu betonu činí 30,6 mm:

Možnost ‚Zohlednit počáteční stav‘ z jiné kombinace zatížení se opět používá pro zohlednění poškození z charakteristické kombinace zatížení:

Výsledkem je průhyb 25,6 mm:

3. Porovnání výsledků

Zatěžovací situace	Nelineární analýza (NL)	Přídavný modul pro návrh betonu	Poměr (NL / Add-on)
Zohlednění poškození z krátkodobého zatížení	22,3	25,6	0,87
Zohlednění poškození z charakteristického zatížení	25,6	30,6	0,84

Rozdíl mezi nelineární analýzou a přístupem náhradních tuhostí v přídavném modulu pro návrh betonu lze vysvětlit následujícím způsobem: Modul používá lineárně elastický materiál a výpočet provádí analyticky přes celý průřez. Poškození je přitom zohledněno globálním rozdělovacím koeficientem, takže výsledky mají tendenci být konzervativní. Naproti tomu nelineární výpočet vychází z modelu FE s nelineárním betonovým materiálovým modelem. Poškození je zde stanoveno pro každý prvek průřezu individuálně a efekty jako Tension Stiffening mohou být lokálně zohledněny. Tím se výrazně realisticky zobrazuje vznik trhlin a rozložení napětí.

4. Závěrečné poznámky

Nelineární výpočet deformace dvoupolového železobetonového nosníku s ohledem na únosnost jasně ukazuje rozdíly oproti klasickým lineárním přístupům v přídavném modulu pro návrh betonu. Nelineární analýza umožňuje realistické zobrazení rozložení napětí v průřezu, zejména v tahové oblasti po vzniku trhlin, a lokálně zohledňuje vliv Tension Stiffening pro každý prvek v průřezu. Paralelně ukazuje přídavný modul návrhu betonu spolehlivý, jednoduchý a zvláště komfortní přístup: Umožňuje zohlednit efekty z krátkodobých zatížení i efekty trvalých zatížení v charakteristických (a také častých) návrhových situacích.