Analyse de déformation non-linéaire d’une poutre en béton armé à deux travées tenant compte du fluage

1. Données d’entrée

Géométrie

• Système statique :

Système : Poutre à deux travées
Portée de la travée 1 : l₁ = 5,0 m
Portée de la travée 2 : l₂ = 4,0 m

• Cotations de la section :

Largeur : b = 1000 mm
Hauteur : h = 160 mm

• Propriétés de calcul :
  • Enrobage béton c_nom = 22,0 mm
  • Armatures longitudinales prévues : Les armatures sont disposées symétriquement en haut et en bas de la section. Dans la couche supérieure et inférieure, il y a 22 barres avec un diamètre de 6,0 mm chacune (A_s,Côté = 6,22 cm²).

Chargement

Les deux travées sont chargées par une charge permanente, et chaque travée est également soumise à une charge variable :

• CC1 : Cas de charge Poids propre : g_k = 1,6 kN/m
• CC2 : Cas de charge Charge d’exploitation dans la travée 1 : q_1,k = 5,0 kN/m
• CC3 : Cas de charge Charge d’exploitation dans la travée 2 : q_2,k = 5,0 kN/m

Pour le calcul de la déformation, seule la situation de projet quasi-permanente est déterminante. Il en résulte les trois combinaisons de charges suivantes :

• CO1 = CC1 + 0,60 × CC2
• CO2 = CC1 + 0,60 × CC2 + 0,60 × CC2
• CO3 = CC1 + 0,60 × CC3

Matériaux

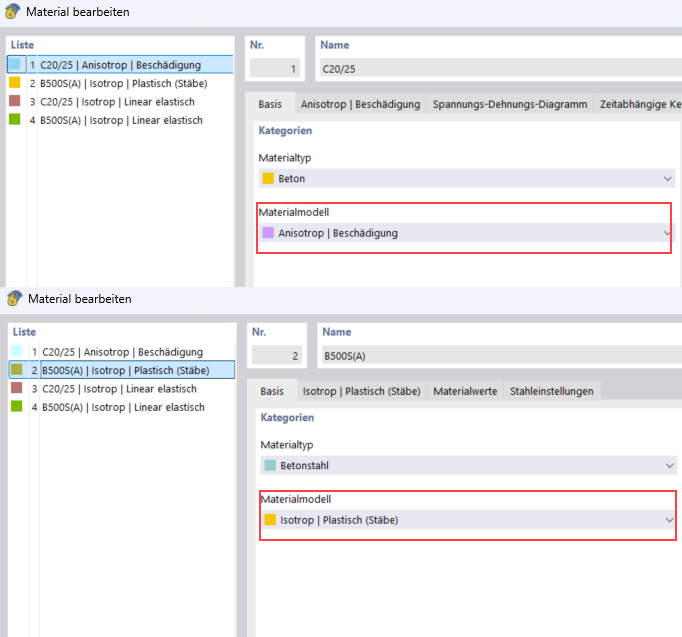
Le béton de classe C20/25 et l'acier de béton armé de classe B500S(A) sont d’abord adoptés depuis la bibliothèque de matériaux. Pour le type de matériau Béton, le modèle de matériau non linéaire Anisotrope | Endommagement est bien adapté pour le calcul de la déformation. Pour le type de matériau Acier de béton armé, le modèle de matériau non linéaire approprié Isotrope | Plastique doit être sélectionné.

• Béton C20/25

Une fois le modèle de matériau défini, l’onglet spécifique « Anisotrope | Détérioration » apparaît :
Définition du diagramme : Dans le cadre de cet exemple, une analyse de déformation doit être effectuée, donc le diagramme « ELS | Valeurs (moyennes) pour la flèche » peut être utilisé.

Région en compression :
Pour l’analyse non linéaire, la région de compression est représentée avec le type de diagramme « Parabole » (selon 3.1.5) et la résistance en compression f_cm.

Raidissement en traction :
Pour le raidissement en traction, l’approche via la résistance en traction résiduelle du béton (Quast | Béton) est sélectionnée.

Dans la région en traction, une courbe de type parabole-rectangle est définie. Avant la fissuration, la courbe suit une forme parabolique, dans laquelle le béton est pleinement impliqué. La résistance en traction calculée du béton f_ct,R lors de la première fissure est présumée être \( f_{ct,R} = k \cdot f_{ct} = 0,6 \cdot 2.200 = 1.320~\text{N/mm}^2 \) (pour une déformation de fissuration calculée ε_cr,R de 0.1‰). Une fois cette déformation de fissuration dépassée, la résistance en traction du béton diminue, et la courbe contrainte-déformation s’aplatit.

La résistance en traction du béton f_ct,R n’est pas une grandeur constante, mais dépend de la déformation de la fibre d’acier déterminante dans l’élément. Elle diminue linéairement lorsque la déformation de fissuration ε_cr,R est dépassée et devient nulle dès que la déformation d’élasticité ε_s de l’acier de béton armé est atteinte.

Cette dépendance entre la résistance en traction du béton et la déformation de l’acier est décrite par le facteur VMB. Pour l’intervalle ε > ε_cr,R, la courbe contrainte-déformation dans la région en traction peut être décrite avec l’équation suivante : \( \sigma_c = VMB \cdot f_{ct,R} \)

Avant la fissuration (ε_s < ε_cr), le facteur de réduction VMB reste à 1,0, ce qui signifie que le béton conserve sa pleine participation dans la région en traction et que la résistance à la traction n'est pas réduite. Il n'y a pas encore de réduction de la participation, car le béton n'est pas encore fissuré. Après avoir atteint la déformation fissuration (ε_cr), le béton commence à perdre son raidissement en traction. Le facteur de réduction VMB diminue. Selon l’exposant de distribution n_vmb, la réduction suit des courbes différentes :
n_vmb = 1,0 : Réduction linéaire.
n_vmb = 2,0 : Réduction plus rapide et plus abrupte.
Après avoir atteint la limite d’élasticité de l’acier de béton, les armatures reprennent toute la contrainte de traction, et le béton ne contribue plus au raidissement en traction. Le facteur de réduction VMB atteint 0.

• Acier de béton armé B500S(A)

Pour l’acier de béton armé, le type de diagramme peut également être ajusté dans l’onglet spécifique. Dans cet exemple, le type de diagramme standard est utilisé.

• Fluage et retrait :

Le fluage est d'abord activé pour le matériau béton dans l’onglet Propriétés dépendantes du temps du béton. Les réglages spécifiques pour le fluage sont ensuite enregistrés dans l’onglet Propriétés dépendantes du temps avancées du béton.

Le retrait n’est pas détaillé : En raison des armatures presque symétriques dans la travée 1 et de la petite différence des armatures dans la travée 2, les courbures dues au retrait ne contribuent que de manière insignifiante à la déformation totale. Le retrait est donc désactivé.

Paramètres pour l’analyse statique

Pour l’analyse non linéaire de la déformation, les paramètres suivants sont utilisés :

• Type d’analyse : Le fluage est représenté linéairement par une courbe contrainte-déformation modifiée. Les valeurs de déformation du béton sont multipliées par le facteur (1 + φ_ef). Le type d’analyse à utiliser est « Analyse statique | Fluage et retrait (linéaire) »
• Modification de la structure : Afin de prendre en compte la rigidité des armatures dès l’analyse, les armatures de barre doivent être activées via une modification de structure pour le béton armé.
• Temps de chargement de fluage : La définition des temps de chargement se fait dans la section Temps.

Paramètres du maillage EF

La longueur d’élément souhaitée des éléments finis a été réglée à 100 mm. De plus, le maillage EF de la section pour l’analyse non linéaire est doté d’un facteur de décalage de 0,50, de sorte qu’un maillage EF plus fin se forme dans la section, permettant un calcul plus précis de l’état de contrainte.

2. Résultats

La déformation issue de l’analyse non linéaire en tenant compte de l’influence du fluage donne, dans la travée 1 à la position x=2,20m, une flèche de 18,2 mm.

La représentation des contraintes de base σ_x le long de la barre montre que la contrainte en traction atteint une valeur maximale de 1,247 N/mm² dans la travée 1 et dans la région des poteaux.

La distribution des contraintes dans la section à la position x=2,20m est illustrée par une coupe :

Comparaison avec les résultats du module complémentaire Vérification du béton

Un calcul de la déformation avec le module complémentaire Vérification béton donne à la position x = 2,20 m une flèche de 25,6 mm.

Un examen plus approfondi du calcul dans le module complémentaire montre que pour la détermination de l’ndomamgement via le coefficient de distribution ζ, les contraintes de la charge de courte durée (sans l’effet de fluage) sont déterminantes :

Pour prendre en compte les effets de la charge de courte durée également dans l’analyse non linéaire, la fonction « Considérer l’état initial » peut être utilisée. Une combinaison de charges sans fluage est d’abord créée. Cette combinaison de charges est ensuite adoptée comme état initial dans la combinaison de charges principale :

Avec ces paramètres, une flèche de 22,3 mm est atteinte.

• Calcul de la déformation pour la situation de projet quasi-permanente avec état fissuré basé sur les charges associées de la situation de projet pour l’ELS

Pour le calcul de la déformation dans la situation de projet quasi-permanente, vous pouvez prendre en compte l’état fissuré déterminant à partir des combinaisons de charges associées (combinaisons de charges quasi-permanentes, combinaisons de charges fréquentes) (pour en savoir plus, consultez cet article technique).

Cela se produit, par exemple, lorsque, au début de la durée de vie, la combinaison de charges fréquente ou caractéristique est critique et qu’au fur et à mesure, jusqu'à la fin de la durée de vie, la combinaison de charges quasi-permanente s’applique.

Vous pouvez facilement configurer cela dans le module complémentaire Vérification du béton en activant l’option correspondante dans la configuration pour l’ELS.

Dans cet exemple, l’endommagement de la combinaison de charges quasi-permanente est déterminant pour le calcul de la déformation dans la combinaison de charges caractéristique. La flèche maximale de la combinaison de charges caractéristique dans le module complémentaire Vérification du béton est de 30,6 mm :

L’option « Considérer l’état initial » d’une autre combinaison de charges est à nouveau utilisée pour prendre en compte l’endommagement de la combinaison de charges caractéristique :

Il en résulte une flèche de 25,6 mm :

3. Comparaison des résultats

Situation de charge	Analyse non linéaire (NL)	Module complémentaire Vérification du béton	Ratio (NL / Module complémentaire)
Considération de l’endommagement dû à la charge de courte durée	22,3	25,6	0,87
Considération de l’endommagement dû à l’action caractéristique	25,6	30,6	0,84

La différence entre l’analyse non linéaire et la méthode des rigidités équivalentes dans le module complémentaire Vérification du béton peut être expliquée comme suit : le module complémentaire utilise un matériau linéaire-élastique et effectue le calcul analytiquement sur l’ensemble de la section. L’endommagement est prise en compte via un coefficient de distribution global, ce qui entraîne généralement des résultats conservateurs. En revanche, l’analyse non linéairee est basé sur un modèle EF avec un modèle de matériau béton non linéaire. L’endommagement est calculée individuellement pour chaque élément de la section, et des effets comme le raidissement en traction peuvent être pris en compte localement. Par conséquent, la fissuration et la distribution des contraintes sont représentées de manière beaucoup plus réaliste.

4. Remarques finales

L’analyse non linéaire de la déformation d’une poutre en béton armé à deux travées, en tenant compte du fluage, met en évidence les différences par rapport aux approches classiques linéaires dans le module complémentaire Vérification du béton. L’analyse non linéaire permet une représentation réaliste de la distribution des contraintes dans la section, en particulier dans la région en traction après la fissuration, et prend en compte l’effet de raidissement en traction localement pour chaque élément dans la section. Parallèlement, le module complémentaire Vérification du béton propose une approche fiable, simple et particulièrement conviviale : il permet de prendre en compte les effets des charges de courte durée ainsi que ceux des charges permanentes dans les situations de projet caractéristiques (et également fréquentes).