Конечные элементы с топологической точки зрения

С помощью RFEM вы можете рассчитывать различные конструктивные элементы, такие как стержневые элементы, пластины, стены, оболочки и тела. Перед выполнением каких-либо расчетов, необходимо создать сетку конечных элементов (FE), которая соответствует требуемым 1D, 2D и 3D элементам.

Анализ КЭ включает в себя разложение конструктивной системы на более мелкие подсистемы, каждая из которых представлена конечными элементами. Для каждого из этих элементов определяются условия равновесия. Этот процесс приводит к формулировке линейной системы уравнений с большим количеством неизвестных переменных. Точность результатов напрямую зависит от степени измельчения конечных элементов. Важно отметить, что более мелкая сетка повышает точность, но также значительно увеличивает время вычисления из-за большого объема обработки данных. Это связано с тем, что для каждого дополнительного узла КЭ необходимо решать дополнительные уравнения.

К счастью, сетка КЭ создается в программе автоматически. Тем не менее, существуют опции, обеспечивающие контроль над процессом генерирования сетки.

Элементы 1D

У элементов стержней предполагается, что сечение во время деформации сохраняет свою плоскую форму. Одномерные стержневые элементы используются для представления балок, ферм, ребер, вантов и жестких соединений. Каждый элемент стержня 1D включает в себя в общей сложности двенадцать степеней свободы - шесть в точке начала и шесть в конечной точке. Эти степени свободы относятся к перемещениям (u_x, u_y, u_z ) и поворотам (φ_x, φ_y, φ_z ).

Если аддон Депланация при кручении активирован, в каждом узле доступна дополнительная степень свободы, которую можно использовать для учета депланации.

В контексте линейного расчета конструкций, растяжение, сжатие и кручение выражаются в виде линейных функций вдоль оси стержня (x), независимо от эффектов изгиба и сдвига. В данном представлении данные эффекты аппроксимируются с помощью полинома третьего порядка по x, который также учитывает влияние касательных напряжений, возникающих в результате действия поперечных сил V_y и V_z. Матрица жесткости K_L (12, 12) характеризует линейную работу данных одномерных элементов. Кроме того, для сценариев с геометрически нелинейными задачами, где осевая сила взаимодействует с изгибом, применяется матрица жесткости K_NL (12, 12).

Для точных расчетов в случаях, связанных со значительными деформациями, рекомендуется повысить точность сетки конечных элементов (FE) для линий, как подробно описано в разделе Уплотнения сетки линий.

Элементы 2D

Обычно четырехугольные элементы служат в качестве двухмерных компонентов в расчете конструкций. В процессе генерирования сетки вводятся треугольные элементы там, где они необходимы. Степени свободы, связанные с угловыми узлами как четырехугольных, так и треугольных элементов, совпадают со степенями свободы, связанными с одномерными элементами, включая перемещение (u_x, u_y, u_z ) и поворот (φ_x, φ_y, φ_z ). Такое расположение обеспечивает совместимость 1D и 2D элементов в узлах. Параметры сначала задаются в местной плоской системе координат элементов, а затем при создании общей матрицы жесткости преобразуются в общую систему координат.

Элементы оболочек (2D) в программе RFEM

Плоские элементы оболочек основаны на теории Миндлина-Рейснера. Графическое изображение на рисунке иллюстрирует элементы подхода. Для прямой связи с элементами стержня, применяется квадратичный стержень в плоскости оболочки (u_x, u_y ). В данном случае промежуточные узлы исключаются, и мы получим четырехузловой элемент с дополнительной степенью свободы φ_x. Данная конфигурация облегчает прямое соединение между стенными элементами и балочными элементами. Кроме того , применяются элементы MITC4 ( смешанная интерполяция тензорных компонентов), представленная Дворкиным и Бате [1]. В их основе используется смешанная техника интерполяции, охватывающая поперечные деформации, повороты сечений и поперечные деформации сдвига.

В настоящее время элементы стержней рассчитываются путем прямого решения дифференциального уравнения расчета второго порядка. Однако, при использовании кручения по Сен-Венану эффекты депланации не учитываются. Расчет мембранных конструкций основан на принципах Бергана. Например, треугольные элементы задаются путем разложения основных функций на три деформации жесткого тела, три условия постоянной деформации и три конкретных линейных градиента напряжения и деформации. В элементе, поле деформации имеет квадратичный характер, в то время как поле напряжений поддерживает линейность. Матрица жесткости элемента K_L затем преобразуется в девять комбинированных параметров типов u_x, u_y, φ_z. Эти компоненты матрицы включены в общую матрицу жесткости (18, 18) вместе с компонентами, учитывающими эффекты изгиба и сдвига, что приводит к концепции Линна-Дхиллона.

Далее в расчете применяются плиты Миндлина, в которых плиты с характерными искажениями сдвига рассчитываются по принципам Тимошенко. который позволяет программе RFEM правильно решать проблемы, связанные как с толстыми, так и с тонкими пластинами (плиты Навье). В геометрически нелинейных случаях разделение напряженно-деформированного состояния на плоское состояние и изгиб со сдвиговым взаимодействием не осуществимо. Взаимодействия между этими состояниями учитываются с помощью матрицы K_NL. В RFEM используется упрощенная, но эффективная версия матрицы K_NL, разработанная под влиянием Целкевича. При этом применяется квадратичная составляющая ε₂ тензора деформаций Грина/Лагранжа ε = ε₁ + ε₂. Предполагается линейное распределение u_z (x,y) при плоском напряженном состоянии и линейное распределение u_x (x,y) и u_y (x,y) при изгибном взаимодействии. Это предположение верно из-за основного влияния взаимодействия, зависящего от первой производной дифференциального уравнения и быстрого уменьшения влияния компонентов более высокого порядка с меньшим дроблением элементов. Правильность данного подхода затем была подтверждена многочисленными численными расчетами.

У элементов оболочки необходимо, чтобы толщина элементов была значительно меньше, чем их длина. Если данное условие не выполняется, то рекомендуется моделировать объекты в виде твердых тел. Кроме того, при использовании элементов оболочек необходимо постепенное введение скручивающих напряжений, поскольку степень свободы поворота вокруг нормали к поверхности очень чувствительна.

Элементы 3D

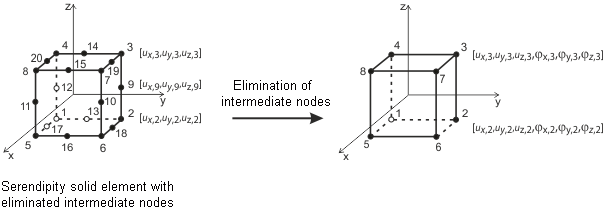
В программе RFEM реализованы следующие 3D-элементы: четырехгранник, пятигранник (призма, пирамида) и шестигранник. Подробную информацию о применяемых элементах и матрицах можно найти в Sevčík 3D конечные элементы с поворотными степенями свободы (на чешском языке, может быть получено по запросу в Dlubal Software).

Объёмный элемент (гексаэдр)

Как правило, для тел все степени свободы вращения должны рассматриваться как критические. Поскольку деформация тела определяется исключительно из векторов перемещения, поворот узла сетки, например, из-за сингулярно введенного кручения, не влияет на деформацию тела.