Mit RFEM können Sie verschiedene Bauteile wie Stabelemente, Platten, Wände, Schalen und Volumenkörper berechnen. Vor der Durchführung von Berechnungen muss ein Finite-Elemente-Netz (FE-Netz) erstellt werden, das den gewünschten 1D-, 2D- und 3D-Elementen entspricht.
Bei der FE-Analyse wird das Tragwerk in kleinere Teilsysteme zerlegt, die jeweils durch finite Elemente dargestellt werden. Für jedes dieser Elemente werden Gleichgewichtsbedingungen festgelegt. Dieser Prozess führt zur Aufstellung eines linearen Gleichungssystems mit zahlreichen unbekannten Variablen. Die Genauigkeit der Ergebnisse wird direkt durch den Verdichtungsgrad in der Netzgröße der finiten Elemente beeinflusst. Es ist wichtig anzumerken, dass ein feineres Netz zwar die Genauigkeit erhöht, aber aufgrund der größeren Datenmenge, die verarbeitet werden muss, auch die Rechenzeit erheblich erhöht. Dies liegt daran, dass für jeden zusätzlichen FE-Knoten weitere Gleichungen gelöst werden müssen.
Glücklicherweise wird das FE-Netz automatisch von der Software generiert. Dennoch gibt es Optionen, mit denen sich der Netzgenerierungsprozess steuern lässt.
1D-Elemente
Bei Stabelementen wird davon ausgegangen, dass der Querschnitt während der Verformung seine ebene Form beibehält. 1D-Stabelemente werden zur Darstellung von Trägern, Fachwerken, Rippen, Seilen und starren Verbindungen verwendet. Jedes 1D-Stabelement umfasst insgesamt zwölf Freiheitsgrade – sechs am Startpunkt und sechs am Endpunkt. Diese Freiheitsgrade beziehen sich auf Verschiebungen (ux, uy, uz) und Drehungen (φx, φy, φz).
Wenn das Wölbkrafttorsions-Add-On aktiviert ist, steht an jedem Knoten ein zusätzlicher Freiheitsgrad zur Verfügung, der zur Berücksichtigung der Wölbung genutzt werden kann.
Im Rahmen der linearen statischen Berechnung werden Zug, Druck und Torsion als lineare Funktionen entlang der Stabachse (x) ausgedrückt, unabhängig von Biege- und Schubwirkungen. Diese Darstellung approximiert diese Effekte mittels eines Polynoms dritter Ordnung in x, das auch den Einfluss von Schubspannungen berücksichtigt, die durch die Schubkräfte Vy und Vz entstehen. Die Steifigkeitsmatrix KL(12, 12) charakterisiert das lineare Verhalten dieser 1D-Elemente. Zusätzlich wird für Szenarien mit geometrisch nichtlinearen Problemen, bei denen die Normalkraft mit der Biegung zusammenwirkt, die Steifigkeitsmatrix KNL(12, 12) verwendet.
Für präzise Berechnungen bei erheblichen Verformungen empfiehlt es sich, die Genauigkeit des Finite-Elemente-Netzes (FE-Netzes) für Linien zu verbessern, wie im Kapitel Liniennetzverdichtungen der Dokumentation beschrieben.
2D-Elemente
In der Regel dienen Viereckelemente als 2D-Komponenten in der statischen Analyse. Der Netzgenerierungsprozess fügt dort, wo es erforderlich ist, Dreieckselemente ein. Die mit den Eckknoten sowohl der Viereck- als auch der Dreieckselemente verbundenen Freiheitsgrade entsprechen denen von 1D-Elementen und umfassen Verschiebung (ux, uy, uz) und Drehung (φx, φy, φz). Diese Anordnung gewährleistet die Kompatibilität zwischen 1D- und 2D-Elementen an Knoten. Die Parameter werden zunächst im lokalen ebenen Koordinatensystem der Elemente definiert und anschließend bei der Erstellung der globalen Steifigkeitsmatrix in das globale Koordinatensystem transformiert.
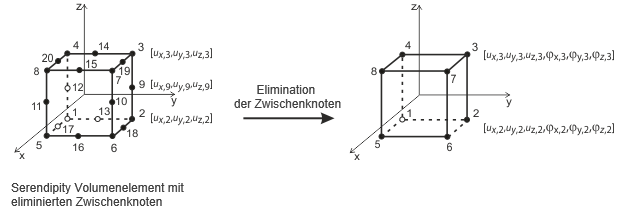
Die planaren Schalenelemente basieren auf der Mindlin/Reissner-Theorie. Die grafische Darstellung in der Abbildung veranschaulicht die Elementansätze. Um eine direkte Verbindung zu Stabelementen herzustellen, wird innerhalb der Schalenebene (ux, uy) ein quadratischer Ansatz gewählt. Diese Wahl macht Zwischenknoten überflüssig, was zu einem Vierknotenelement mit einem zusätzlichen Freiheitsgrad φx führt. Diese Konfiguration ermöglicht eine direkte Kopplung zwischen Wand- und Trägerelementen. Zusätzlich werden MITC4-Elemente (Mixed Interpolation of Tensorial Components) verwendet, wie sie von Dvorkin und Bathe [1] eingeführt wurden. Sie basieren auf einer gemischten Interpolationstechnik, die Querverformungen, Querschnittsdrehungen und Querschubdehnungen umfasst.
Derzeit werden Stabelemente durch direkte Lösung der Differentialgleichung II. Ordnung verarbeitet. Bei Verwendung der Saint-Venant-Torsion werden Wölbungseffekte jedoch nicht berücksichtigt. Die Analyse von Membranen basiert auf den Bergan-Prinzipien. So werden beispielsweise Dreieckselemente definiert, indem die Grundfunktionen in drei Verformungen starrer Körper, drei konstante Dehnungsbedingungen und drei spezifische lineare Gradienten von Spannung und Dehnung zerlegt werden. Innerhalb eines Elements zeigt das Verformungsfeld quadratisches Verhalten, während das Spannungsfeld linear bleibt. Die Elementsteifigkeitsmatrix KL wird dann in neun kombinierte Parameter der Typen ux, uy, φz transformiert. Diese Matrixkomponenten werden zusammen mit den Komponenten, die zu Biege- und Schubwirkungen beitragen, in die Gesamtsteifigkeitsmatrix (18, 18) integriert, was zum Lynn/Dhillon-Konzept führt.
Anschließend umfasst die Analyse die Anwendung von Mindlin-Platten, wobei Platten mit charakteristischen Schubverzerrungen nach den Prinzipien von Timoshenko analysiert werden. Dies ermöglicht es RFEM, Probleme sowohl bei dicken als auch bei dünnen Platten (Navier-Platten) korrekt zu lösen. Bei geometrisch nichtlinearen Problemen ist die Aufteilung der Spannungs-Dehnungs-Bedingungen in einen ebenen Zustand und Biegung mit Schubinteraktionen nicht möglich. Die Interaktionen zwischen diesen Zuständen werden über die KNL-Matrix berücksichtigt. RFEM verwendet eine vereinfachte, aber effektive Version der KNL-Matrix, die von den Ansätzen von Zienkiewicz beeinflusst ist. Es wird die quadratische Komponente ε2 des Green/Lagrange-Dehnungstensors ε = ε1 + ε2 verwendet. Es wird eine lineare Verteilung von uz(x, y) unter der ebenen Spannungsbedingung sowie lineare Verteilungen von ux(x, y) und uy(x, y) während der Biegeinteraktion angenommen. Diese Annahme ist gültig, da der primäre Einfluss der Interaktion von der ersten Ableitung der Differentialgleichung abhängt und der Einfluss von Komponenten höherer Ordnung bei kleineren Elementunterteilungen rapide abnimmt. Zahlreiche numerische Analysen haben die Richtigkeit dieses Ansatzes bestätigt.
Beim Umgang mit Schalenelementen ist es unerlässlich, dass die Dicke der Elemente deutlich geringer ist als ihre Ausdehnung. Ist diese Bedingung nicht erfüllt, empfiehlt es sich, Objekte stattdessen als Volumenkörper zu modellieren. Darüber hinaus sollte bei der Verwendung von Schalenelementen eine schrittweise Einführung von Torsionsspannungen erfolgen, da der Rotationsfreiheitsgrad um die Flächennormale sehr empfindlich ist.
3D-Elemente
In RFEM sind folgende 3D-Elemente implementiert: Tetraeder, Pentaeder (Prisma, Pyramide) und Hexaeder. Ausführliche Informationen zu den verwendeten Elementen und Matrizen finden Sie in Sevčík: 3D Finite Elements with Rotational Degrees of Freedom (auf Tschechisch, auf Anfrage bei Dlubal Software erhältlich).
Im Allgemeinen müssen bei Volumenkörpern alle Rotationsfreiheitsgrade als kritisch betrachtet werden. Da die Verformung eines Volumenkörpers ausschließlich durch die Verschiebungsvektoren bestimmt wird, hat die Drehung eines Netzknotens, beispielsweise aufgrund einer singulär eingeführten Torsion, keinen Einfluss auf die Verformung innerhalb des Volumenkörpers.