Za pomocą programu RFEM można analizować różne elementy konstrukcyjne, takie jak elementy prętowe, płyty, ściany, powłoki i bryły. Przed przeprowadzeniem obliczeń konieczne jest wygenerowanie siatki elementów skończonych (ES), która odpowiada żądanym elementom 1D, 2D i 3D.
Analiza MES obejmuje podział układu konstrukcyjnego na mniejsze podukłady, z których każdy jest reprezentowany przez elementy skończone. Dla każdego z tych elementów tworzone są warunki równowagi. Proces ten prowadzi do sformułowania liniowego układu równań z wieloma nieznanymi zmiennymi. Na dokładność wyników ma bezpośredni wpływ stopień zagęszczenia rozmiaru siatki elementów skończonych. Należy pamiętać, że drobniejsza siatka zwiększa dokładność, ale także znacznie wydłuża czas obliczeń ze względu na przetwarzanie większej ilości danych. Dzieje się tak, ponieważ dla każdego dodatkowego węzła ES należy rozwiązać dodatkowe równania.
Na szczęście siatka ES jest generowana automatycznie przez oprogramowanie. Istnieją jednak opcje, które zapewniają kontrolę nad procesem generowania siatki.
Elementy 1D
W przypadku elementów prętowych przyjmuje się, że przekrój zachowuje swój płaski kształt podczas odkształcenia. Elementy prętowe 1D są wykorzystywane do reprezentowania belek, kratownic, żeber, kabli i połączeń sztywnych. Każdy element prętowy 1D ma łącznie dwanaście stopni swobody – sześć w punkcie początkowym i sześć w punkcie końcowym. Te stopnie swobody odnoszą się do przemieszczeń (ux ,uy, uz )i obrotów (φx, φy, φz ).
Po aktywowaniu rozszerzenia Skręcanie skrępowane w każdym węźle dostępny jest dodatkowy stopień swobody, który można wykorzystać do uwzględnienia deplanacji.
W przypadku analizy liniowej rozciąganie, ściskanie i skręcanie są wyrażane jako funkcje liniowe wzdłuż osi pręta (x), niezależnie od efektów zginania i ścinania. Przedstawienie to przybliża te efekty za pomocą wielomianu trzeciego rzędu w x, który uwzględnia również wpływ naprężeń tnących wynikających z sił tnących Vy i Vz. Macierz sztywności KL (12, 12) charakteryzuje liniowe zachowanie tych elementów 1D. Dodatkowo, w przypadku scenariuszy dotyczących problemów geometrycznie nieliniowych, w których oddziałuje siła osiowa i zginanie, stosowana jest macierz sztywności KNL (12, 12).
W celu zapewnienia precyzyjnych obliczeń w przypadkach związanych ze znacznymi odkształceniami, zaleca się zwiększenie dokładności siatki elementów skończonych (ES) dla linii, jak opisano w rozdziale zagęszczenia siatki liniowej dokumentacji.
Elementy 2D
Elementy czworokątne zazwyczaj pełnią rolę komponentów 2D w analizie statyczno-wytrzymałościowej. Proces generowania siatki powoduje wprowadzanie elementów trójkątnych tam, gdzie są one potrzebne. Stopnie swobody powiązane z węzłami narożnymi elementów czworobocznych i trójkątnych są zgodne z stopniami swobody elementów 1Di obejmują przemieszczenie (ux , u y, uz ) i obrót (φx, φy, φz ). Takie rozmieszczenie zapewnia kompatybilność między elementami 1D i 2D w węzłach. Parametry te są początkowo definiowane w lokalnym płaskim układzie współrzędnych elementów, a następnie podczas tworzenia globalnej macierzy sztywności przekształcane na globalny układ współrzędnych.
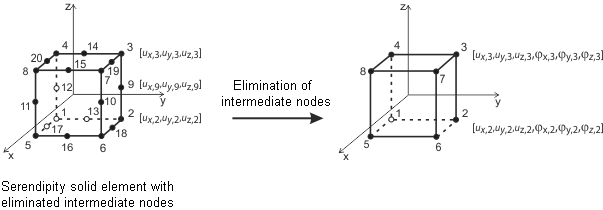
Płaskie elementy powłokowe opierają się na teorii Mindlina/Reissnera. Graficzne przedstawienie na rysunku ilustruje podejścia elementów. Do bezpośredniego łączenia z elementamiprętowymi przyjmuje się podejście kwadratowe w płaszczyźnie powłoki (ux , u y). Wybór ten eliminuje węzły pośrednie, dzięki czemu powstaje element czterowęzłowy z dodatkowym stopniem swobody φx. Ta konfiguracja ułatwia bezpośrednie połączenie między elementami ściennymi a elementami belkowymi. Dodatkowo zastosowano elementy MITC4 (Mieszkana interpolacja składowych tensorycznych ) wprowadzone przez Dvorkina i Bathe'a [1]. Opierają się one na technice interpolacji mieszanej obejmującej odkształcenia poprzeczne, obroty przekroju i poprzeczne odkształcenia ścinające.
Obecnie elementy prętowe są traktowane poprzez bezpośrednie rozwiązywanie równania różniczkowego analizy drugiego rzędu. Jednak w przypadku stosowania skręcania według Saint Venanta efekty deplanacji nie są uwzględniane. Analiza membran opiera się na zasadach Bergana. Na przykład, elementy trójkątne są definiowane poprzez podział funkcji podstawowych na trzy deformacje ciała sztywnego, trzy stałe warunki odkształcenia oraz trzy określone liniowe gradienty naprężeń i odkształceń. Pole deformacji w elemencie zachowuje się kwadratowo, podczas gdy pole naprężeń zachowuje liniowość. Macierz sztywności elementu KL jest następnie przekształcana na dziewięć połączonych parametrów typówux , u y, φz. Zgodnie z koncepcją Lynna/Dhillona, te komponenty macierzy są uwzględniane w ogólnej macierzy sztywności (18, 18), wraz z komponentami odpowiedzialnymi za efekty zginania i ścinania.
Następnie w analizie wykorzystywane są płyty Mindlina, w których płyty z charakterystycznymi odkształceniami od ścinania są analizowane z wykorzystaniem teorii Timoshenki'. Dzięki temu program RFEM może poprawnie rozwiązywać problemy związane zarówno z grubymi, jak i cienkimi płytami (płyty Naviera). W przypadku geometrycznie nieliniowych zagadnień, podział warunków naprężeniowo-odkształceniowych na stan płaski oraz zginanie ze ścinaniem nie jest możliwy. Interakcje między tymi stanami są uwzględniane za pomocą macierzy KNL. Program RFEM wykorzystuje uproszczoną, ale efektywną wersję macierzy KNL, na którą wpływ mają metody Zienkiewicza. Stosowana jest kwadratowa składowa ε2 tensora odkształceń Greena/Lagrange'a ε = ε1 + ε2. Zakłada się liniowy rozkład uz (x, y) w płaskim stanie naprężenia oraz zakłada liniowy rozkład ux (x, y) i uy (x, y) podczas zginania. Założenie to jest uzasadnione ze względu na to, że główny wpływ interakcji zależy od pierwszej pochodnej równania różniczkowego oraz ze względu na szybką redukcję wpływu składowych wyższego rzędu o mniejszych podziałach elementu. Liczne analizy numeryczne potwierdziły poprawność tego podejścia.
W przypadku elementów powłokowych istotne jest, aby grubość elementów była znacznie mniejsza niż ich wydłużenie. Jeżeli warunek ten nie jest spełniony, zaleca się modelowanie obiektów jako brył. Ponadto w przypadku elementów powłokowych należy stopniowo wprowadzać naprężenia skręcające, ponieważ stopień swobody obrotu względem normalnej do powierzchni jest bardzo czuły.
Elementy 3D
W programie RFEM zaimplementowane są następujące elementy 3D: czworościan, pięciościan (graniastosłup, ostrosłup) i sześcian. Szczegółowe informacje na temat zastosowanych elementów i macierzy można znaleźć w publikacji Elementy skończone ze stopniami swobody obrotu Sevčík 3D (w języku czeskim, na życzenie w firmie Dlubal Software).
Zasadniczo w przypadku brył należy traktować wszystkie stopnie swobody obrotu jako krytyczne. Ze względu na to, że odkształcenie bryły jest określane wyłącznie na podstawie wektorów przemieszczenia, obrót jednego węzła siatki, np. wskutek przyłożenia momentu skręcającego, nie wpływa na odkształcenie w bryle.