使用RFEM,您可以分析各种结构组件,如杆件、板、墙、壳和实体元素。在进行任何计算之前,必须生成与所需的1D、2D和3D元素相对应的有限元(FE)网格。
有限元分析涉及将结构体系分解为较小的子系统,每个子系统由有限元表示。对每个元素建立平衡条件。这一过程导致形成了一个包含众多未知数的线性方程组。结果的精确度直接受到有限元网格尺寸细化程度的影响。需要注意的是,较精细的网格可以提高准确性,但由于需要处理的大量数据,计算时间也会显著增加。这是因为每个附加的有限元节点都需要解算额外的方程。
幸运的是,软件会自动生成有限元网格。然而,仍有选项可以控制网格生成过程。
1D 元素
对于杆件元素,假设截面在变形过程中保持其平面形状。1D杆件元素用于表示梁、桁架、肋、缆索和刚性连接。每个1D杆件元素包含总共十二个自由度——在其起始点和终点各有六个自由度。这些自由度涉及位移(ux, uy, uz)和旋转(φx, φy, φz)。
如果扭转翘曲附加模块被激活,则在每个节点有一个额外的自由度,可以用来考虑翘曲。
在线性结构分析的背景下,拉伸、压缩和扭转沿杆件轴(x)以线性函数表示,并且独立于弯曲和剪切效应。此表示使用x中的三阶多项式来近似这些效应,这也考虑了剪切力Vy和Vz引起的剪切应力的影响。刚度矩阵KL(12, 12)描述了这些1D元素的线性行为。此外,对于轴向力与弯曲相互作用的几何非线性问题,使用刚度矩阵KNL(12, 12)。
如果涉及重大变形的情况下进行精确计算,建议提高线的有限元(FE)网格的精度,详细信息请参见文档的第Line Mesh Refinements章。
2D 元素
在结构分析中,通常使用四边形元素作为2D组件。网格生成过程在需要的地方引入三角形元素。四边形和三角形元素角节点相关的自由度与1D元素的自由度一致,包含位移(ux, uy, uz)和旋转(φx, φy, φz)。这种安排确保了节点处1D和2D元素之间的兼容性。参数首先在元素的局部平面坐标系中定义,然后在创建全局刚度矩阵时转换为全局坐标系。
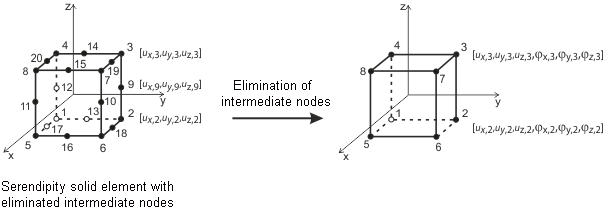
平面壳元素基于Mindlin/Reissner理论。图中的图形表示了元素的处理方法。为了直接连接杆件元素,壳平面内采用了方形处理方法(ux, uy)。这种选择消除了中间节点,形成了四节点元素,并添加了一个自由度φx。这种配置促进了墙元素和梁元素之间的直接耦合。此外,使用了MITC4元素(即Mixed Interpolation of Tensorial Components),这种方法由Dvorkin和Bathe引入[1]。它们依赖于一种混合插值技术,涵盖了横向变形、截面旋转和横向剪切应变。
目前,杆件元素通过直接求解二阶分析微分方程进行处理。然而,当使用Saint Venant扭转时,不考虑翘曲效应。膜的分析基于Bergan原则。例如,通过将基本函数分解为三个刚体变形、三个恒应变条件以及应力和应变的三个特定线性梯度,定义了三角形元素。在元素内,变形场表现为二次行为,而应力场保持线性。元素刚度矩阵KL随后被转换为九个类型为ux, uy, φz的组合参数。这些矩阵组件被纳入到整体刚度矩阵(18, 18)中,连同弯曲和剪切效应的部分,共同形成Lynn/Dhillon概念。
随后,使用Mindlin板的分析,其中带有特殊剪切变形的板使用Timoshenko原则进行分析。这允许RFEM正确解决与厚板和薄板(Navier板)相关的问题。在几何非线性问题的情况下,无法将应力-应变条件分为平面状态和弯曲与剪切相互作用。通过KNL矩阵考虑这些状态之间的相互作用。RFEM使用了一种简化但有效的KNL矩阵版本,受Zienkiewicz方法影响。使用Green/Lagrange应变张量ε的平方分量ε2。假设平面应力状态下的uz(x, y)呈线性分布,弯曲相互作用期间的ux(x, y)和uy(x, y)呈线性分布。这种假设是有效的,因为相互作用的主要影响依赖于微分方程的一阶导数,而随着较小元素划分,使得高阶分量的影响迅速降低。大量的数值分析验证了这种方法的正确性。
在处理壳元素时,至关重要的是元素的厚度必须显著小于其延伸。如果条件不满足,建议将对象建模为实体。此外,在使用壳元素时,应逐步引入扭转应力,因为围绕表面法线的旋转自由度高度敏感。
3D 元素
RFEM中实现了以下3D元素:四面体、五面体(棱柱、棱锥)和六面体。有关应用元素和矩阵的详细信息,可以参考Sevčík的《带旋转自由度的三维有限元》(捷克语,如有需要可从Dlubal软件获取)。
通常,必须将所有旋转自由度视为固体的重要组成部分。由于固体的变形仅由位移矢量决定,因此例如由于单独引入的扭转引起的网格节点的旋转不会影响固体内部的变形。