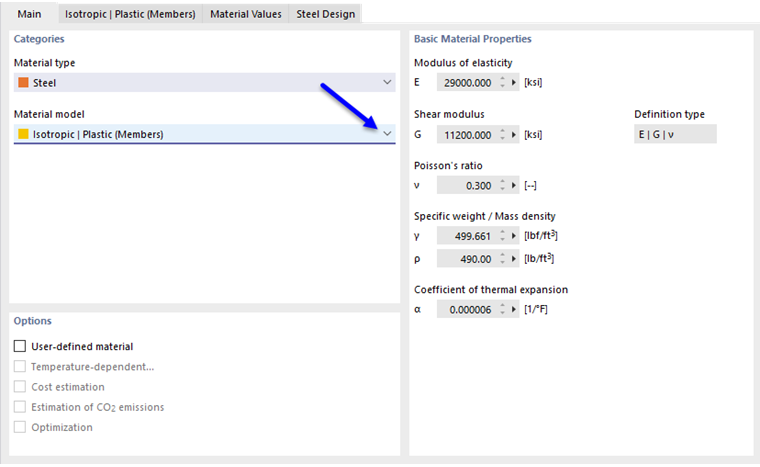
Если аддон Нелинейная работа материала активирован (требуется дополнительная лицензия) в разделе Модель - основные данные, в списке моделей материала будут доступны и другие опции для выбора, кроме 'Изотропной | Линейная упругая' и 'ортотропная | Линейно-упругие' модели материалов.
При использовании нелинейных моделей материала в программе RFEM, выполняется итерационный расчет. В зависимости от модели материала определяется различное соотношение между напряжениями и деформациями.
Жёсткость конечных элементов многократно корректируется до тех пор, пока не будет соблюдено требуемое соотношение напряжения и деформации. Настройка параметров всегда выполняется для всей поверхности или тела. Поэтому мы рекомендуем при оценке напряжений всегда использовать тип сглаживания Константа на элементах сетки.
Некоторые модели материалов в RFEM обозначаются 'Пластическая', а другие - 'Нелинейная упругая'.
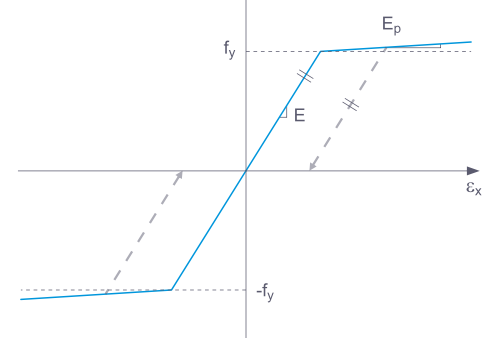
Если конструктивный элемент с нелинейно упругим материалом высвобождается снова, деформация возвращается тем же путем. При полном разгружении деформаций не остается.
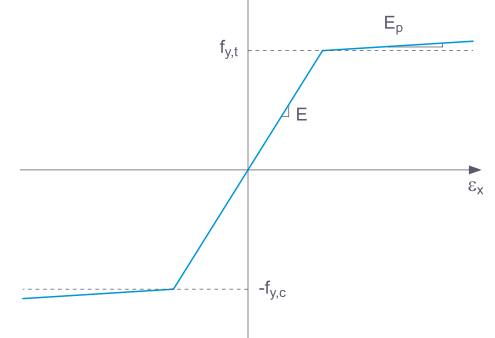
При разгрузке конструктивного элемента с помощью модели материала Пластическая , деформация остается после полной разгрузки.
Основную информацию о нелинейных моделях материалов можно найти в технической статье, описывающей {%><https://www.dlubal.com/ru/podderzhka-i-obuchenije/podderzhka/baza-znanij/000968 Законы текучести при изотропной нелинейной упругой модели модель материала.]]
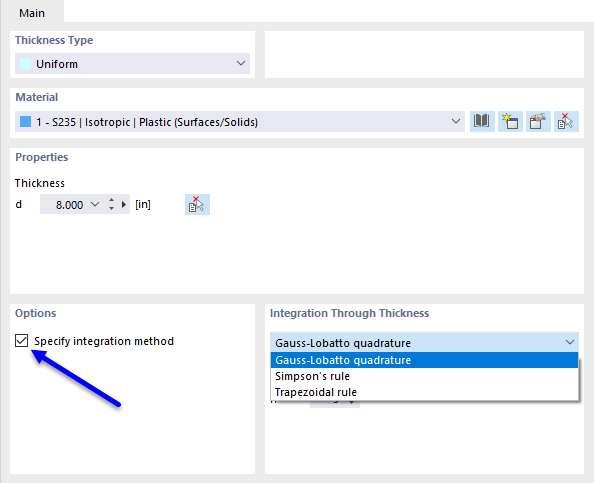
Внутренние силы и моменты в плитах с нелинейным материалом являются результатом численного интегрирования напряжений по толщине d плиты. Чтобы задать метод интеграции для толщины, выберите возможность Укажите метод интеграции в диалоговом окне 'Изменить толщину'. В программе доступны следующие методы интеграции:
- Квадратура Гаусса-Лобатто
- Правило Симпсона
- Трапециевидное правило
Кроме того, можно указать 'Количество точек интеграции' от 3 до 99 в зависимости от толщины пластины.
Изотропная пластичная (стержни)
При выборе {}Изотропной | Пластические стержни в раскрывающемся списке 'Модель материала' включена вкладка для ввода нелинейных параметров материала.
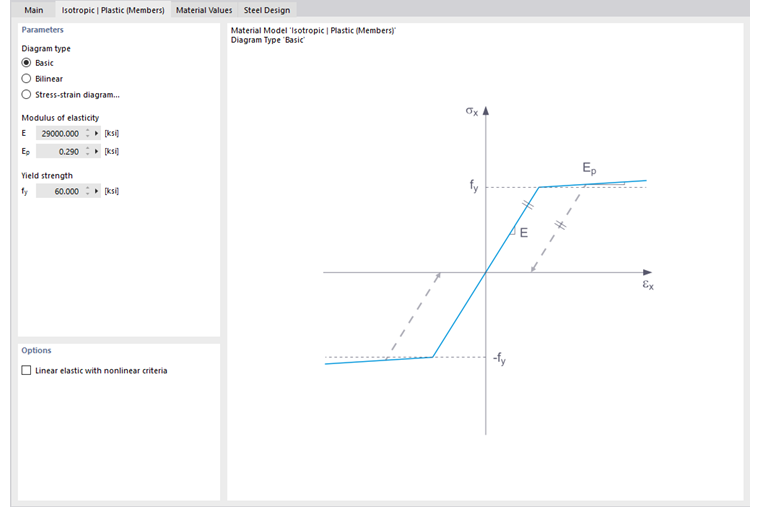
В этой вкладке вы задаете диаграмму напряжения-деформации. Для лицензирования программы затем доступны следующие возможности:
- Basic
- Билинейный
- Рабочая диаграмма
Если выбрано Основное ', RFEM использует билинейную модель материала. Для модуля упругости E и предела текучести fy используются значения из базы данных материалов. По числовым причинам ветвь графика не является точно горизонтальной, а имеет небольшой наклон Ep.
Если вы хотите изменить значения предела текучести и модуля упругости, активируйте флажок «Пользовательский материал» во вкладке 'Основные данные'.
Для билинейного задания можно также ввести значение для Ep.
Более сложные соотношения между напряжением и деформацией можно задать с помощью «Диаграммы напряжения-деформации». При выборе данной опции, отображается вкладка 'Диаграмма напряжения-деформации'.
Определите точку для зависимости напряжения-деформации в каждой строке таблицы. Вы можете выбрать, как будет продолжена диаграмма после последней задающей точки, в списке 'Конец диаграммы' под диаграммой:
В случае 'Разрыв', напряжение после последней заданной точки скачет обратно к нулю. 'Текучесть' означает, что напряжение остается постоянным при увеличении деформации. 'Непрерывный' означает, что график продолжается с наклоном последнего сечения.
Изотропная пластичная (поверхности/тела)
При выборе функции «Изотропная | Пластичная (поверхности/тела)» в раскрывающемся списке 'Модель материала' включена вкладка для ввода нелинейных параметров материала.
Wählen Sie zunächstdie 'Spannungsversagenshypothese' aus. Zur Auswahl stehen diese Hypothesen:
Сначала выберите 'гипотезу разрушения напряжения'. Для выбора доступны следующие гипотезы:
- von Mises (критерий текучести фон Мизеса)
- По Треске (критерий текучести Треска)
- Друкер-Прагер
- Моор-Кулон
При выборе расчета «фон Мизес», в диаграмме напряжения-деформации будет использоваться следующее напряжение:
Поверхности:
Объемы:
Согласно гипотезе «Треска» применяется следующее напряжение:
Поверхности:
Объемы:
Согласно гипотезе Друкера-Прагера, применяется для поверхностей и тел следующее напряжение:
Согласно гипотезе «Мора-Кулона» для поверхностей и тел используется следующее напряжение:
Изотропная нелинейная упругая (стержни)
Функциональность данной модели в основном соответствует модели материала «Изотропная пластическая (стержни)». Разница лишь в том, что после снятия нагрузки не остается пластической деформации.
Изотропная нелинейная упругая (поверхности/тела)
Функциональность данного метода соответствует модели материала изотропная пластическая (поверхности/тела). Разница лишь в том, что после снятия нагрузки не остается пластической деформации.
Изотропное повреждение (поверхности/тела)
В отличие от других моделей материалов, диаграмма напряжения-деформации у этой модели материала не направлена против начала координат. Таким образом, с помощью данной модели материала можно отобразить, например, свойства сталефибробетона. Подробную информацию о моделировании сталефибробетона вы найдете в технической статье Определение свойств материала сталефибробетона железобетонные.
В данной модели материала изотропная жесткость уменьшается со скалярным параметром повреждения. Данный параметр повреждения определяется по кривой напряжений, заданной на Диаграмме. При этом не учитывается направление главных напряжений; скорее всего, разрушение происходит в направлении эквивалентной деформации, которое также включает в себя третье направление, перпендикулярное плоскости. Область растяжения и сжатия тензора напряжений рассматривается отдельно. В каждом случае применяются разные параметры повреждения.
«Размер элемента-ориентира» определяет, как деформация в области трещины масштабируется к длине элемента. При нулевом значении по умолчанию масштабирование не выполняется. Таким образом, свойства материала сталефибробетона моделируются реалистично.
Более подробная информация о теоретических основах модели материала 'изотропное повреждение' находится в технической статье, описывающей [https://www.dlubal.com/ru/podderzhka-i-obuchenije/podderzhka/baza-znanij 001461 Повреждение нелинейной модели материала.
Ортотропная пластическая (поверхности)/ортотропная пластическая (тела)
Модель материала в соответствии с "Tsai-Wu" объединяет свойства пластичности с ортотропными свойствами. Это позволяет моделировать специальные материалы с анизотропными характеристиками, такие как армированный волокном пластик или древесина.
Когда материал достигает пластификации, считается, что напряжения остаются неизменными. Перераспределение затем осуществляется в соответствии с жесткостями, доступными в отдельных направлениях.
ПФИ
ПФИ
Упругая область соответствует Ортотропной модели материала. Для пластической зоны применяется следующее условие текучести по Tsai-Wu:
Поверхности (2D):
FORMEL (английская версия)
Тела (3D):
FORMEL (английская версия)
Все прочности требуется задать в качестве положительных значений.
Вы можете рассматривать критерий напряжения как эллиптическую поверхность в шестимерном пространстве напряжений. Если один из трех компонентов напряжения применяется в качестве постоянного значения, то поверхность можно спроецировать в трехмерное пространство напряжений.
Если значение для fy (σ) по уравнению Цая-Ву, плоское напряженное состояние, меньше чем 1, то напряжения находятся в зоне упругости. Пластическая зона достигается при fy (σ) = 1. Значения выше 1 не допускаются. Поскольку работа модели идеально-пластичная, жесткость здесь отсутствует.