本文所阐述的观点就是不能在任何结构分析中,直接盲目的对任何一个钢结构壳结构中都是通过有限元建模、添加荷载最后点击计算按钮。 在大对数情况下对于简单的结构,有非常多的简化计算和分析方法。 这类解析分析方法即手算方法相对于数值分析方法有很大的优势,例如节省计算时间、简化计算书等。 例如对于部分的钢结构仓储设备的翘曲稳定性验算的计算篇幅可以简化为一张A4纸的页面。 相对于数值计算的计算书,解析方法大大的简化了计算书的篇幅长度。
还有在另外一些大量的情况下,使用数值分析方法不仅可行而且手算方法也同样优越。 下文将阐述在何种情况下,结构分析使用数值分析方法结果可能精确,需要再次使用数值分析的情况。
下文将阐述在有限元软件 RFEM 中,按照MNA/LBA线性翘曲分析方法验算钢结构板壳结构的翘曲稳定性。 并且在分析时可以设置钢结构材料的非线性属性。
按照欧洲规范 EN 1993-1-6 验算翘曲失稳
在欧洲规范 3, EN 1993-1-6 中有 3 种计算钢结构壳体翘曲稳定性的方法。 本节将按照计算精度的要求以及结构工程师的要求逐条分析计算结果。
按照容许应力进行的翘曲稳定性验算
依据极限应力强度为基础的翘曲验算时最经典的验算方法,该方法在工程领域设计薄板壳体结构时被广大的结构工程师所选用。 对于专业的结构工程师此方法较为简单,并且对于计算机性能的要求较低或者直接通过手算既可以满足计算要求。
此方法最大的问题是,对于壳体结构来说为使其产生最典型的翘曲屈曲形式而施加于结构上的荷载类型和大小几乎得不到较为经济的计算结果。 此外在使用此方法时有可能使工程师产生的一种错觉,那就是壳体结构的翘曲失稳只取决于相关结构中的最大应力值。 如果仅仅按照极限应力值决定翘曲稳定性的话,那么如果在壳体结构的周边设置纵向加劲肋将不会起到稳定性的作用,因为其应力值并没有发生本质的减小。 然而实际情况是,如果壳体结构添加适当的加劲肋,厚度相等的情况下,其翘曲稳定性较未添加加劲肋的板壳的大大增加。
MNA/LBA 线性翘曲数值分析方法
下文将阐释如何使用该方法计算钢结构壳体结构。 壳体稳定 MNA/LBA 线性翘曲分析方法较极限容许应力分析方法要求工程师所需要掌握的理论知识更多。 另外有限元数值分析时对计算机的要求也更高,因为此方法按照线性翘曲分析 LBA 方法,并且在分析时可以设置钢结构材料的非线性属性(MNA)。
如果采用有限元方法进行分析时,按照作者观点,本方法是验算翘曲稳定性最为合理的一种方法。 其原因是当使用有限元软件按照 MNA/LBA 线性翘曲分析方法计算时,计算机内存的占用率比较均匀而且不是太高,计算耗时也不是特别多。 如果按照线性弹性方法计算壳体结构的内力,然后按照极限容许应力分析方法计算,那么此方法并不连续,因为当前的性能高效的有限元软件例如RFEM 可以完全胜任更加复杂的计算并且可以直接计算壳体结构的承载能力极限状态。
GMNIA 一般非线性翘曲数值分析方法
GMNIA 一般非线性翘曲数值分析方法是一种确定壳体结构翘曲稳定性分项结果最稳定的方法。 此方法可以考虑内力、几何尺寸以及材料属性非线性并添加缺陷进行后续计算。
由于在添加设置壳体结构的初始缺陷(初始翘曲模型)时难度较大,因此使用该方法时所要求的壳体结构稳定性分析专业知识水平较高。 如果没有掌握此专业知识,强烈建议不使用此 GMNIA 一般非线性翘曲数值分析方法进行验算。 另外在计算过程中所占用的计算机系统资源非常大。 因此要求安装软件的计算机符合软件要求的最低配置要求,以便于计算过程中每个荷载步都可以按照非线性计算临界荷载,并且能够由预屈曲曲线的临界位置的下端“跳跃”到屈曲后阶段的屈曲曲线。
本方法在本文将不再具体阐述,因为在具体的实际工程中几乎不会使用。 更多相关信息请参见 Herbert Schmidt [2]在钢结构 2012 年发表的文章,其中简要介绍了使用 GMNIA 方法进行设计时遇到的困难。
按照 MNA/LBA 线性翘曲分析方法验算翘曲稳定性例题
输入结构体系
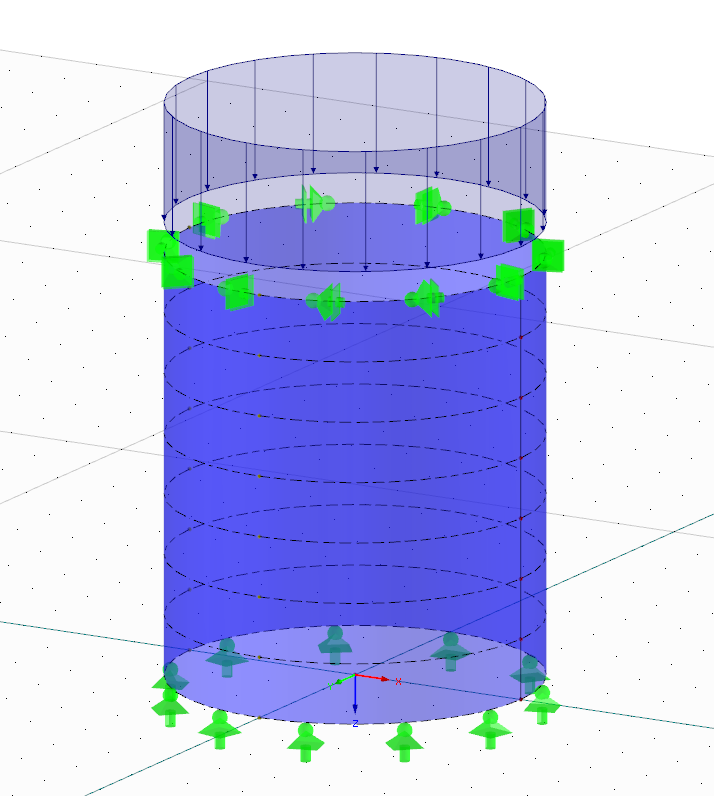
本例题需要验算图 01 所示的钢结构壳体结构的翘曲稳定性。 本实例所处理的基本上为此类结构最典型的情况,如果不需要按照有限元分析方法计算钢结构壳体的稳定性时,大多情况下用此方法。 专题报告的主要目的就是演示如何按照 MNA/LBA-线性翘曲分析验算翘曲稳定性,使用简单例题便于解释和说明。
单元大小是壳体结构非线性计算或分叉分析中的一个重要主题,因为选择不当的有限元网格设置会导致结果错误。 在本文涉及的专业文献中有关于此问题,介绍了如何计算结果能够收敛的方法以及所建议使用的公式等。
使用有限元软件 RFEM 计算
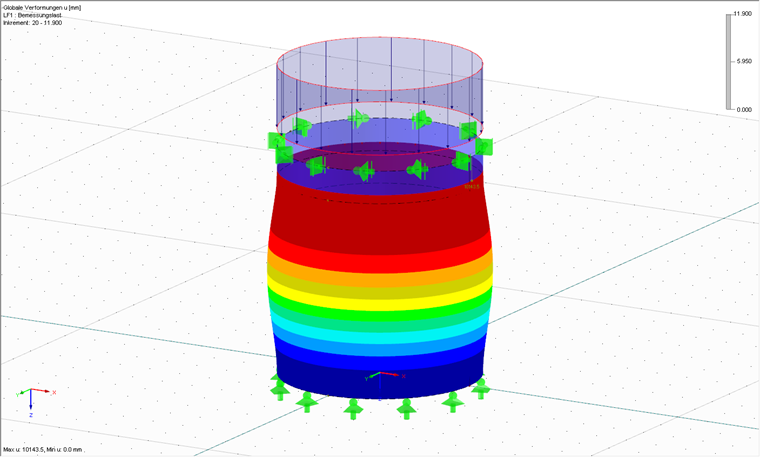
在建模完成、输入荷载并设置相应的有限元网格划分后就可以使用有限元软件RFEM 进行计算。 首先还需要计算分析实际的非线性属性。 此分析的目的是计算壳体在所受到的荷载直到结构发生塑性极限承载力破坏所需乘的荷载放大系数。 为了在有限元软件 RFEM 中使用材料的非线性属性,需要使用另外一个附加模块RF-MAT NL 计算材料的属性。 或者,可以进行线弹性计算;然后使用[3]中的公式(8.24)可以近似计算塑性参考承载力。 图 02 显示了达到塑性参考承载力 rRpl = 11,90 后的变形系统。
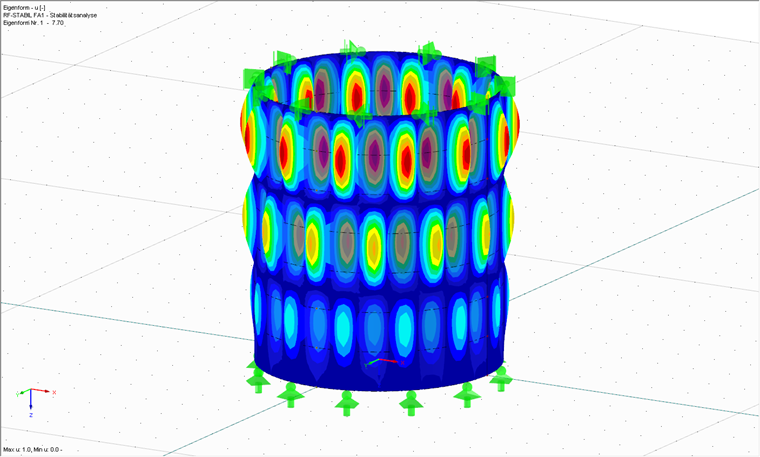
最后将计算线性翘曲分析,并且任意选择其计算顺序。 也可以将此步骤计算调到前面,最后再进行按照线性翘曲分析 MNA/LBA 继续验算。 线性屈曲分析的目的是计算荷载放大系数,荷载在达到放大倍数后的数值后,壳体将达到完全翘曲破坏。 另外还需要附加模块 RF-STABILITY 用于计算线性翘曲分析和几何非线性计算。 注意,此种计算不是 GMNIA-计算方法。 图 03 显示了当特征值 rRcr = 7.70 时所考虑的壳的第一个模态。
板的屈曲分析
下文将阐述翘曲验算的具体步骤。 需要特别注意的是四个独立的翘曲参数,对于大多数实际施工情况,可以按照[3]中的附录 D 来确定。
MNA 塑性极限承载力系数:
rRpl = 11,9
LBA 翘曲稳定性系数:
rRcr = 7,70
壳体换算长细比:
弹性缺陷系数:
塑性发展系数:
βov = 0.60
翘曲曲线指数:
ηov = 0.60
完全塑性极限长细比:
部分塑性极限长细比:
翘曲折减系数:
翘曲验算:
计算的主要问题是将程序获得的结果分类为一种典型的屈曲情况。 本例题的荷载情况比较简单:分析的情况基本上可以归类为完全径向上的受压翘曲失稳问题。 分析的情况基本上可以归类为完全径向上的受压翘曲失稳问题。 因此可以按照欧洲钢结构规范EN 1993-1-6 [3] , 附录 D 1.2 中规定的不相关的翘曲参数进行计算。
按照线性翘曲分析 MNA/LBA 验算钢结构板壳结构的翘曲稳定性的计算结果是荷载增大系数。 本例题的计算结果为1.515。 其具体数学意义是: 壳体结构所能承受的最大荷载还可以增加 50 % 才能达到临界屈曲破坏。
如果按照以应力计算为基础的分析方法进行计算,本例工况下的荷载增大系数为 1,398。如在上文阐述的,对于这种典型的翘曲工况下在受到径向的受压荷载工况下发生翘曲屈曲,如果按照线性翘曲分析MNA/LBA的分析方法与按照有限元数值分析不会有明显的差别。 这里还需要再次强调一下,这里有发生局部荷载传递位置或者在支座位置处出现应力集中的可能。
概述总结
功能强大、操作简单的有限元软件,例如 RFEM 极大的简化了工程师在处理壳体结构翘曲稳定性计算的各种问题。 通过使用 MNA/LBA 线性翘曲分析方法验算钢结构板壳结构的翘曲稳定性所得出的计算结果通常情况下更加符合实际情况也更加经济。
此外还需要说明的是,并不是所有的壳体结构都适合进行有限元分析,因为对于典型类型的翘曲形式可以使用数值分析方法,其计算书可以大大简化并且同时可以得到更加经济的计算结果。 但是,如果工程师在设计实践中遇到无法归类为典型屈曲工况的情况,那么使用附加模块 RF-STABILITY 和 RF-MAT NL替代标准方法。