V našem článku také důrazně nedoporučujeme používat jednoduše pro každou ocelovou skořepinu model konečných prvků a po nanesení zatížení kliknout na tlačítko „Výpočet“. Ve většině případů je tento postup ve výsledku náročnější, protože v návrhové praxi je pro posouzení častých a jednoduchých případů k dispozici řada analytických metod. V případě těchto analytických metod se jedná o vzorce pro ruční výpočty, jejichž výhodou je navíc úsporná, jednoduchá dokumentace. U mnohých nádrží nám pro posouzení na boulení bude stačit jedna normostrana A4. V případě analýzy metodou konečných prvků (MKP) takto úsporné dokumentace dosáhnout nelze.
V řadě případů je ovšem použití metody konečných prvků opodstatněné a měli bychom ji upřednostnit před ručním výpočtem. Níže uvádíme pouze několik příkladů, kdy výpočet MKP považujeme za důvodný:
Následně posoudíme ocelovou skořepinu na boulení v programu RFEM metodou MNA/LBA. Bude se tedy uvažovat nelineární materiálové chování oceli.
Posouzení boulení podle EN 1993-1-6
EN 1993-1-6 uvádí tři možnosti, jak lze posuzovat ocelové skořepiny na boulení. V následujícím oddílu si tyto možnosti stručně popíšeme a vyhodnotíme je z hlediska nároků na výpočetní techniku i na zhotovitele návrhu.
Navrhování podle výpočtu napětí
Ověření únosnosti při boulení na základě výpočtu napětí lze považovat za klasickou metodu, kterou již někdy zvolil asi každý statik zabývající se posouzením skořepin. Pro odborníka se jedná o jednoduchou metodu s velmi malými nebo dokonce s vůbec žádnými nároky na výpočetní techniku vzhledem k tomu, že se často pracuje se vzorci pro ruční výpočty.
Zásadním problémem této metody posouzení je víceméně nemožnost dosáhnout hospodárných výsledků v případě, že se zatěžovací situace u skořepinových konstrukcí značně odchylují od klasických tvarů boulení. Navíc může tato metoda zavádět na nesprávnou cestu, pokud se budeme domnívat, že únosnost skořepinové konstrukce při boulení závisí pouze na působících napětí. Pokud by tomu bylo tak, pak by vyztužení stěny skořepiny například podélnými žebry sotva přinášelo užitek, protože se tak napětí nijak výrazně nezmenší. Ve skutečnosti je ovšem únosnost při boulení mnohem vyšší u vhodně vyztužené skořepiny než u nevyztužené skořepiny se stejnou tloušťkou stěny.
Navrhování podle globální numerické analýzy MNA/LBA
Tento postup použijeme níže pro posouzení skořepiny. Při posouzení pomocí analýzy MNA/LBA je jistě třeba mít lepší povědomí o stabilitě skořepin než v případě posouzení na základě výpočtu napětí. Uživatel by měl mít také k dispozici o něco výkonnější výpočetní techniku, protože správné použití této metody předpokládá provedení lineární pružné analýzy rozdvojení tvaru (LBA) a materiálově nelineární analýzy (MNA).
Jsme toho názoru, že tato metoda posouzení představuje nejvhodnější způsob posouzení na boulení, pokud se má provést analýza konečných prvků. Při návrhu pomocí analýzy MNA/LBA je totiž také využití výpočetní techniky konsekventní, přičemž na uživatele nejsou kladeny příliš vysoké nároky. Jestliže stanovíme vnitřní síly skořepiny lineárně pružným výpočtem a následně je použijeme pro posouzení boulení na základě výpočtu napětí, tak využití výpočetní techniky není příliš logické vzhledem k tomu, že výkonné programy jako RFEM jsou schopny stanovit také únosnost skořepinové konstrukce.
Navrhování podle globální numerické analýzy GMNIA
Analýza GMNIA pro stanovení dostatečné stability skořepiny je asi nejdůslednější metoda ověření únosnosti při boulení. Vnitřní síly se přitom stanoví geometricky a materiálově nelineární analýzou s uvážením imperfekcí.
Tato metoda vyžaduje znamenité znalosti stabilitní problematiky skořepinových konstrukcí, protože již jen správné stanovení imperfekcí (před kritickým zatížením) je nadmíru obtížné. Pokud uživatel takové povědomí o problematice nemá, měl by od návrhu pomocí analýzy GMNIA upustit. Také na výpočetní techniku klade tato metoda posouzení značné nároky. Používaný programový systém musí zvládnout v průběhu nelineárního výpočtu provést analýzu rozdvojení tvaru při každé úrovni zatížení, a odhalit tak případný „skok“ z předkritického do pokritického úseku křivky.
Touto koncepcí se v našem příspěvku nebudeme podrobněji zabývat, protože se domníváme, že pro statické návrhy v praxi má jen stěží význam. Rádi bychom ovšem odkázali na článek Herberta Schmidta [2] ve sborníku Stahlbau-Kalender 2012, který přehledně shrnuje veškeré obtíže posouzení metodou GMNIA.
Příklad ověření únosnosti při boulení metodou MNA/LBA
Zadání statického systému
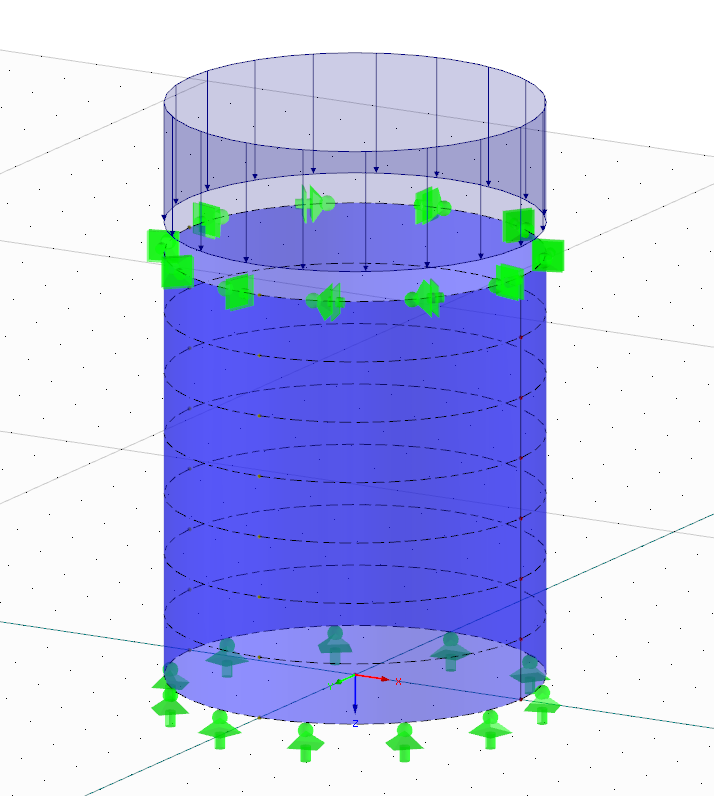
V našem příkladu posoudíme na boulení ocelovou skořepinu znázorněnou na obr. 01. V podstatě se přitom jedná o typický případ, u kterého by se odborník zběhlý v navrhování ocelových skořepin stěží rozhodl pro analýzu konečných prvků. Protože je však hlavním cílem našeho článku přiblížit čtenáři problematiku posouzení boulení metodou MNA/LBA, je třeba zvolit co možná nejjednodušší příklad.
Důležitým bodem nelineárních výpočtů, respektive analýz rozdvojení tvaru skořepinových konstrukcí je velikost prvku, protože nevhodně zvolené nastavení sítě konečných prvků může vést ke zkresleným výsledkům. V odborné literatuře lze najít různé kontrolní vzorce, přičemž asi nejvhodnější je (malá) analýza konvergence.
Výpočet pomocí programu RFEM
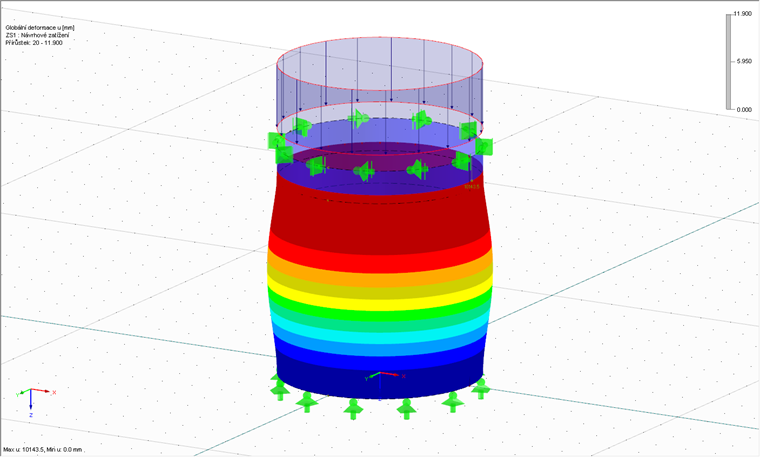
Po zadání modelu a zatížení a po vhodném nastavení sítě konečných prvků můžeme spustit výpočet pomocí programu RFEM. Nejdříve proběhne materiálově nelineární analýza. Jejím cílem je stanovit referenční plastickou únosnost, tedy takový součinitel kritického zatížení, při kterém dochází k celkovému plastickému porušení skořepiny. Ideální je mít licenci k přídavnému modulu RF-MAT NL, protože jen tak máme v programu RFEM k dispozici nelineární materiálové vlastnosti. Další možné řešení představuje lineárně pružný výpočet a následné přibližné stanovení referenční plastické únosnosti ze vztahu (8.24) v normě [3]. Na obr. 02 můžeme vidět stav deformace po dosažení faktoru referenční plastické únosnosti rRpl = 11,90.
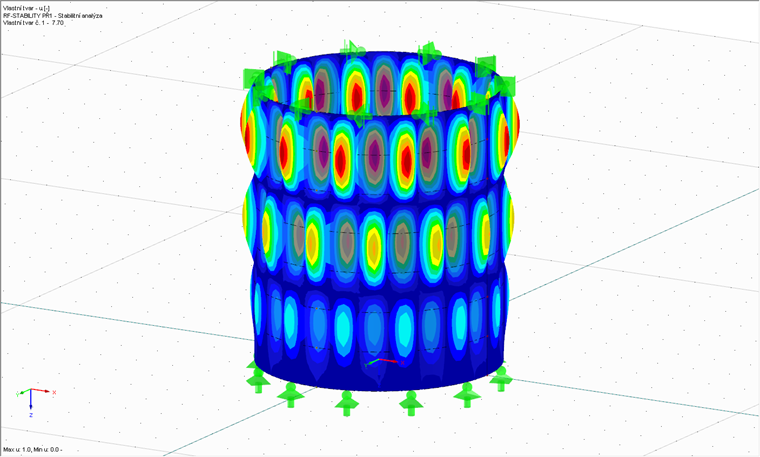
Následuje lineární analýza rozdvojení tvaru. Pořadí analýz jsme přitom zvolili náhodně. Postupovat můžeme i opačně, tedy provést nejdříve tuto analýzu a následně pak analýzu MNA. Při lineární analýze rozdvojení tvaru rovněž chceme stanovit součinitel kritického zatížení, tentokrát se ovšem jedná o faktor, při kterém dochází k boulení skořepiny bez imperfekcí. Je přitom nezbytné mít k dispozici přídavný modul RF-STABILITY, který slouží k lineárním analýzám rozdvojení tvaru i ke geometricky nelineárním výpočtům, čímž nemáme na mysli výpočty GMNIA. Na obr. 03 je znázorněn první vlastní tvar posuzované skořepiny pro vlastní hodnotu rRcr = 7,70.
Ověření únosnosti při boulení
Celkové posouzení boulení představíme níže. Zvláštní pozornost je přitom třeba věnovat čtyřem na sobě nezávislým parametrům boulení, které ve většině případů ze stavební praxe lze stanovit podle přílohy D normy [3].
Referenční plastická únosnost jako výsledek analýzy MNA:
rRpl = 11,9
Součinitel kritického zatížení stanovený při analýze LBA:
rRcr = 7,70
Poměrná štíhlost skořepiny:
Redukční součinitel pružné imperfekce:
Součinitel plastické oblasti:
βov = 0,60
Interakční exponent:
ηov = 0,60
Mezní poměrná štíhlost při stlačení:
Mezní relativní štíhlost v plastické oblasti:
Součinitel vzpěrnosti při boulení:
Posouzení boulení:
Hlavním problémem posouzení je zařazení výsledků z programu do některého z klasických případů boulení. V našem příkladu je řešení vzhledem k zatížení velmi jednoduché: jedná se téměř čistě o boulení v osovém tlaku. Nezávislé parametry boulení se tak vypočítají podle přílohy D 1.2 normy EN 1993-1-6 [3].
Výsledkem ověření únosnosti při boulení metodou MNA/LBA je součinitel kritického zatížení. V našem příkladu činí 1,515. To znamená, že by se zatížení skořepiny mohlo zvýšit ještě o 50 %.
Pokud při návrhu vycházíme z výpočtu napětí, dospějeme v našem příkladu k součiniteli kritického zatížení 1,398, což dokazuje, že u klasických případů boulení, jakým je i boulení při osovém tlaku, nevede numerická analýza MNA/LBA k žádnému výraznému navýšení. Na tomto místě je ovšem třeba znovu upozornit, že situace je jiná v případě koncentrace napětí v důsledku lokálního působení zatížení nebo bodových podpor.
Závěr
Moderní, vysoce výkonné a přitom uživatelsky přívětivé programy pro výpočty metodou konečných prvků, jako je program RFEM, nesmírně usnadňují práci statikům při ověřování dostatečné únosnosti skořepin při boulení. Při důslednějším používání výpočetní techniky v případě výpočtů metodou MNA/LBA lze také zpravidla dosáhnout realističtějších, a tím většinou i hospodárnějších výsledků.
Je ovšem také třeba podotknout, že nikoli u každé skořepinové konstrukce je vhodné zvolit analýzu metodou konečných prvků, protože pro klasické případy boulení se nabízí dobré analytické postupy, které jsou nenáročné na dokumentaci a přitom mohou vést k podobně hospodárným výsledkům. Jestliže se ovšem v návrhové praxi setkáme s případy, které nelze přiřadit k žádnému klasickému případu boulení, pak analýza konečných prvků metodou MNA/LBA v programu RFEM a jeho přídavných modulech RF-STABILITY a RF-MAT NL představuje vážnou alternativu ke klasickým postupům.