En este artículo, también recomendamos encarecidamente no simplemente crear un solo modelo de EF para cada capa de acero, configurar las cargas y luego presionar "Calcular". En la mayoría de los casos, este procedimiento conlleva un trabajo adicional, ya que se encuentran disponibles numerosos métodos analíticos para la verificación para casos simples que son comunes en la práctica del diseño. Estos métodos analíticos, las fórmulas de cálculo manual, también tienen la gran ventaja de ahorrar espacio y de una documentación sencilla. Para algunos contenedores, el análisis de pandeo de la placa se puede realizar en una página A4. Esta documentación que ahorra espacio no es posible con un análisis de EF.
Sin embargo, también hay numerosos casos en los que el uso de un análisis de elementos finitos tiene sentido y debería preferirse a un cálculo manual. Los siguientes puntos son solo algunos ejemplos de casos en los que tiene sentido utilizar un cálculo de EF:
En el siguiente texto, el cálculo de pandeo de una carcasa de acero se realiza utilizando RFEM según el concepto MNA/LBA. Por lo tanto, se aplica el comportamiento del material no lineal del acero.
Análisis de pandeo de placas según EN 1993-1-6
En EN 1993-1-6, se presentan tres opciones para realizar un análisis de pandeo de placas para conchas de acero. En esta sección, se enumeran brevemente y se evalúan con respecto a los requisitos de la tecnología informática, así como con respecto a los requisitos impuestos al ingeniero de diseño.
Análisis de pandeo de placas basado en tensiones
El análisis de pandeo de placas basado en tensiones se considera el método de análisis estándar que casi todos los ingenieros han utilizado al realizar el diseño de la carcasa. Este método puede ser clasificado como sencillo para un ingeniero experto y los requisitos informáticos son o bien muy bajos o inexistentes, ya que se utilizan frecuentemente fórmulas para el cálculo manual.
Un problema importante de este método de análisis es que difícilmente se lograrán resultados económicos para estructuras de cáscara con situaciones de carga que se desvían considerablemente de los modos de pandeo estándar. Además, como usuario de este concepto, se encuentra en el camino equivocado con este método, porque podría pensar fácilmente que la seguridad de pandeo de la placa de la estructura del armazón solo depende de las tensiones que se produzcan. Si ese fuera el caso, el endurecimiento de la pared de una carcasa mediante, por ejemplo, nervios longitudinales tendría poco beneficio, ya que esto no reduce significativamente las tensiones. En realidad, la seguridad de pandeo de la placa de una carcasa hábilmente rígida es mucho mayor que la de una carcasa sin arriostrar del mismo espesor de pared.
Análisis de pandeo de placas basado en el cálculo numérico mediante el cálculo global de MNA/LBA
Este método se utilizará para el siguiente diseño de carcasa. Un cálculo de MNA/LBA ciertamente requiere que el usuario tenga algo más de conocimiento previo en la estabilidad de la carcasa que en el caso del método de diseño basado en esfuerzos. Además, la técnica de cálculo debería ser más potente, ya que para la correcta aplicación de este método es necesario realizar un análisis de bifurcación elástica lineal (LBA) y un análisis de material no lineal (MNA).
En opinión del autor, este método de cálculo es la forma más eficaz de realizar el análisis de pandeo de la placa si el cálculo se va a realizar utilizando el análisis de EF. La justificación de esto es que para un diseño que utiliza el concepto MNA/LBA, la tecnología informática se utiliza de forma coherente sin esperar demasiado esfuerzo por parte del usuario. Si los esfuerzos internos del cuerpo se calculan en elástico lineal para usarlos en el análisis de pandeo de placas basado en esfuerzos, la tecnología informática se utilizará de manera demasiado inconsistente, ya que programas potentes como RFEM también pueden determinar la capacidad de carga de la placa. estructura de la cáscara.
Análisis de pandeo de la placa basado en el cálculo numérico mediante el cálculo de GMNIA global
Un análisis GMNIA para determinar la estabilidad suficiente de la cáscara es probablemente el método más consistente de análisis de pandeo de placas. Por tanto, los esfuerzos internos se calculan geométrica y materialmente de forma no lineal, utilizando imperfecciones.
Este método requiere un excelente conocimiento previo sobre la estabilidad de la cáscara por parte del usuario, ya que, entre otras cosas, el enfoque correcto de las imperfecciones (pre-pandeo) es muy difícil. Si el usuario no tiene estos conocimientos previos, debe evitarse en cualquier caso el proceso de diseño con el concepto GMNIA. Además, se imponen exigencias sustanciales a la tecnología informática cuando se utiliza este método. Por tanto, el sistema de programa utilizado debe poder realizar un análisis de bifurcación para cada paso de carga del análisis no lineal para, en su caso, detectar un "salto" desde la trayectoria subcrítica pre-pandeo a la trayectoria supercrítica post-pandeo.
Este concepto no se explicará más aquí, ya que, en opinión del autor, tiene poca importancia para la práctica del diseño. Para obtener más información, consulte el artículo de Herbert Schmidt [2] en el Calendario de construcción en acero de 2012, que ofrece una buena visión general de las dificultades que se enfrentan al utilizar el cálculo según el método GMNIA.
Ejemplo de análisis de pandeo de placas utilizando el método MNA/LBA
Entrada del sistema estructural
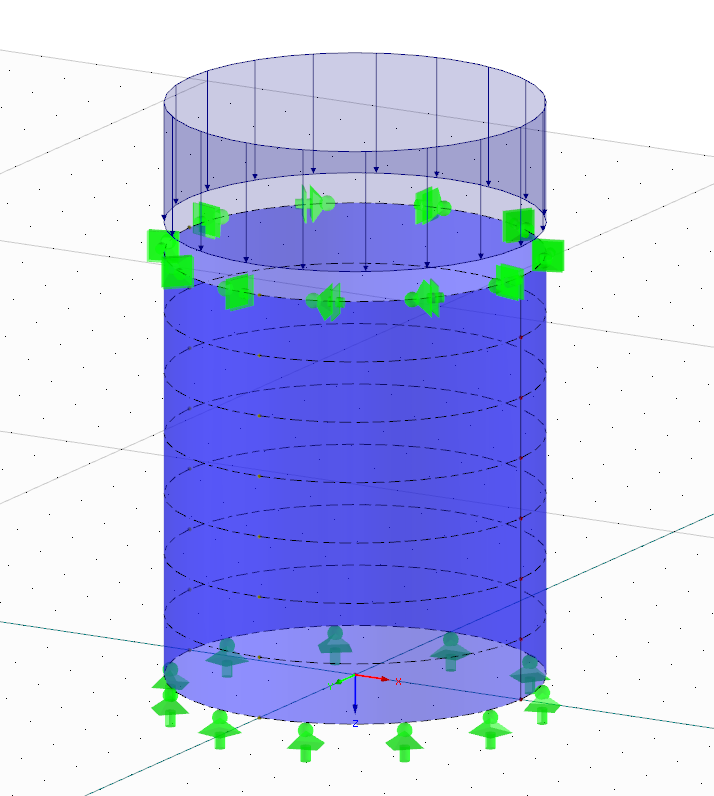
La carcasa de acero que se muestra en la Figura 01 se diseñará para pandeo. En principio, esta estructura es un caso típico en el que un ingeniero familiarizado con el diseño de carcasas de acero difícilmente consideraría un análisis de EF. Dado que el objetivo principal de este artículo es familiarizar al lector con el tema del análisis de pandeo de placas según el concepto MNA/LBA, se utilizará un ejemplo lo más simple posible.
Un tema importante en los cálculos no lineales o los análisis de bifurcación de estructuras de caparazón es el tamaño del elemento, ya que los ajustes de malla de EF seleccionados desfavorablemente pueden dar lugar a resultados falsificados. En la literatura especializada, existen varias fórmulas para el cálculo aproximado, donde el estudio (pequeño) de convergencia es el enfoque más adecuado.
El cálculo con RFEM
Después de introducir el modelo y la carga y seleccionar los ajustes de malla de EF adecuados, se puede iniciar el cálculo con RFEM. Primero, se realiza el análisis no lineal del material. El objetivo de este análisis es la resistencia plástica de referencia (es decir, el factor de carga crítico al que fallaría plásticamente toda la carcasa). El módulo adicional RF-MAT NL se utiliza idealmente, ya que en RFEM solo están disponibles las propiedades no lineales del material. Alternativamente, se puede realizar un cálculo elástico lineal; entonces la resistencia plástica de referencia se puede calcular aproximadamente usando la fórmula (8.24) de [3]. La figura 02 muestra el sistema deformado después de alcanzar la resistencia plástica de referencia rRpl = 11,90.
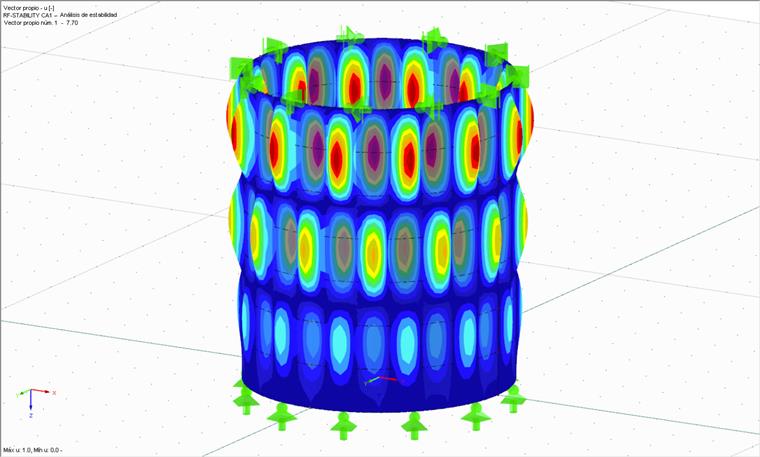
Posteriormente, se realiza el análisis de bifurcación lineal donde la secuencia se eligió arbitrariamente aquí. También es posible realizar este análisis primero y luego continuar con el método MNA. El objetivo del análisis de bifurcación lineal es también obtener un factor de carga crítico, pero esta vez uno que provocaría el pandeo de la cáscara perfecta. Esto requiere el módulo adicional RF-STABILITY, con el que se pueden realizar análisis de bifurcación lineal y cálculos geométricamente no lineales. Esto no se refiere a los cálculos de GMNIA. La figura 03 muestra la forma del primer modo de la capa considerada para el valor propio de rRcr = 7.70.
Análisis de abolladura
El análisis de pandeo de la placa se muestra en su conjunto en el siguiente texto. Se debe prestar especial atención a los cuatro parámetros de pandeo independientes, que se pueden determinar para la mayoría de los casos prácticos de construcción de acuerdo con el Anexo D en [3].
Resistencia plástica de referencia de MNA:
rRpl = 11,9
Factor de carga crítica de LBA:
rRcr = 7,70
Grado de esbeltez:
Coeficiente de reducción por imperfección elástica:
Factor de multiplicación de plástico:
βov = 0,60
Exponente de interacción de la curva de pandeo:
ηov = 0,60
Grado límite de esbeltez totalmente plástico:
Esbeltez limitante parcialmente plástico:
Coeficiente de reducción para pandeo:
Análisis de pandeo de placas:
El problema principal del diseño es clasificar los resultados obtenidos por el programa en uno de los casos típicos de pandeo. En el caso que nos ocupa, es muy sencillo debido a la carga: Se trata de un pandeo puro por presión en los meridianos. Por tanto, se calculan los parámetros de pandeo independientes según el anexo D 1.2 de EN 1993-1-6 [3].
El resultado del análisis de pandeo de la placa según el método MNA/LBA es un factor de carga crítico. En el ejemplo que se muestra aquí, es 1,515. Esto quiere decir: La carga del proyectil se podría incrementar más del 50%.
Si el análisis se basa en el concepto basado en tensiones, esto daría como resultado un factor de carga crítica de 1.398, lo que muestra que para los casos de pandeo típicos, como el pandeo por presión meridiana considerado aquí, la placa de base numérica no obtiene beneficios adicionales. Análisis de pandeo según el método MNA/LBA. Cabe señalar, como ya se mencionó, que esto es diferente tan pronto como las introducciones de cargas locales o los apoyos conducen a concentraciones de tensiones.
Conclusión
Los programas FEM modernos, potentes y fáciles de usar, como RFEM, facilitan significativamente el trabajo de un ingeniero calculador al realizar el cálculo de la seguridad de pandeo suficiente de una carcasa. Como resultado del uso más consistente de la tecnología informática en el concepto MN/LBA, generalmente se pueden lograr resultados más realistas y, por lo tanto, más económicos.
También se debe mencionar que un análisis de EF no es aconsejable para todas las estructuras de cáscara, ya que se encuentran disponibles buenos métodos analíticos para casos de pandeo típicos, lo que puede conducir a una documentación reducida y a resultados igualmente económicos. Sin embargo, si el ingeniero encuentra casos en la práctica de diseño que no se pueden asignar a un caso de pandeo típico, un análisis de EF según el concepto MNA/LBA con RFEM con los módulos adicionales RF-STABILITY y RF-MAT NL es un verdadero desafío. alternativa a los métodos estándar.