In diesem Artikel wird auch ausdrücklich empfohlen, nicht für jede Stahlschale einfach nur ein FE-Modell zu erzeugen, Lasten aufzusetzen und anschließend auf "Rechnen" zu drücken. In den meisten Fällen führt dieses Vorgehen zu einem Mehraufwand, da für in der Bemessungspraxis häufig vorkommende einfache Fälle zahlreiche analytische Methoden für die Nachweisführung zur Verfügung stehen. Diese analytischen Methoden, die sogenannten Handrechenformeln, haben außerdem den großen Vorteil einer platzsparenden und einfachen Dokumentation. Für manchen Behälter ist es möglich, den Beulsicherheitsnachweis auf einer DIN-A4-Seite zu führen. Eine solch platzsparende Dokumentation ist mit einer FE-Analyse nicht möglich.
Es gibt aber auch zahlreiche Fälle, bei denen der Einsatz einer Finite-Elemente-Analyse Sinn macht und einer Handrechnung vorgezogen werden sollte. Die nachfolgenden Punkte sind nur einige beispielhafte Fälle, in denen es sinnvoll ist, auf eine FE-Berechnung zurückzugreifen:
Nachfolgend soll eine stählerne Schale gegen Beulen mit Hilfe von RFEM nach dem MNA/LBA-Konzept nachgewiesen werden. Es wird also ein nichtlineares Materialverhalten des Stahls angesetzt.
Beulsicherheitsnachweise nach EN 1993-1-6
In der EN 1993-1-6 werden drei Möglichkeiten aufgezeigt, einen Beulsicherheitsnachweis für stählerne Schalen zu führen. In diesem Abschnitt sollen diese kurz aufgelistet und bewertet werden hinsichtlich der Anforderungen an die Rechentechnik sowie an den planenden Ingenieur.
Spannungsbasierter Beulsicherheitsnachweis
Der spannungsbasierte Beulsicherheitsnachweis gilt als das klassische Nachweisverfahren, welches wohl jeder Ingenieur, der bereits eine Schalenbemessung durchgeführt hat, auch schon verwendet hat. Dieses Verfahren kann für einen fachkundigen Ingenieur als einfach eingestuft werden und die Anforderungen an die Rechentechnik sind entweder sehr gering oder gar nicht vorhanden, da hier häufig mit Handrechenformeln gearbeitet wird.
Ein großes Problem dieses Nachweisverfahrens besteht darin, dass bei Schalentragwerken mit erheblich von den klassischen Beulformen abweichenden Belastungssituationen wirtschaftliche Ergebnisse kaum zu erreichen sind. Außerdem wird man als Anwender dieses Konzeptes eigentlich vom Verfahren selbst auf eine falsche Fährte gelockt, da man leicht meinen könnte, die Beulsicherheit des Schalentragwerkes ist lediglich von den auftretenden Spannungen abhängig. Wenn dies so wäre, würde eine Aussteifung einer Schalenwand beispielsweise durch Längsrippen kaum etwas bringen, da die Spannungen so nicht signifikant verringert werden. In Wirklichkeit ist die Beulsicherheit einer geschickt ausgesteiften Schale aber viel höher als bei einer unausgesteiften Schale mit der gleichen Wanddicke.
Numerisch gestützter Beulsicherheitsnachweis mittels globaler MNA/LBA-Berechnung
Dieses Verfahren soll für die im Nachfolgenden zu bemessende Schale verwendet werden. Eine MNA/LBA-Berechnung erfordert vom Anwender sicher etwas mehr Hintergrundwissen zur Schalenstabilität als das spannungsbasierte Bemessungsverfahren. Auch sollte die Rechentechnik etwas leistungsfähiger sein, da für eine korrekte Anwendung dieses Verfahrens eine lineare elastische Verzweigungsanalyse (LBA) und eine materiell nichtlineare Berechnung (MNA) durchzuführen sind.
Nach Meinung des Verfassers stellt dieses Bemessungsverfahren die sinnvollste Art des Beulsicherheitsnachweises dar, sofern mittels FE-Analyse gerechnet werden soll. Die Begründung hierfür ist, dass beim Nachweis mittels MNA/LBA-Konzept die Rechentechnik auch konsequent genutzt wird, ohne dass dem Anwender zu viel Aufwand zugemutet wird. Berechnet man die Schnittgrößen der Schale linear elastisch, um diese dann für den spannungsbasierten Beulsicherheitsnachweis zu verwenden, nutzt man eigentlich die Rechentechnik zu inkonsequent, da leistungsfähige Programme wie RFEM in der Lage sind, auch die Tragfähigkeit des Schalentragwerks zu bestimmen.
Numerisch gestützter Beulsicherheitsnachweis mittels globaler GMNIA-Berechnung
Eine GMNIA-Berechnung zur Feststellung einer ausreichenden Schalenstabilität ist wohl die konsequenteste Methode eines Beulsicherheitsnachweises. Hierbei werden die Schnittgrößen geometrisch und materiell nichtlinear unter Ansatz von Imperfektionen berechnet.
Dieses Verfahren erfordert vom Anwender hervorragendes Hintergrundwissen zur Schalenstabilität, da unter anderem der korrekte Ansatz von Imperfektionen (Vorbeulmuster) sehr schwierig ist. Ist dieses Hintergrundwissen beim Anwender nicht vorhanden, sollte auf jeden Fall auf eine Nachweisführung mit dem GMNIA-Konzept verzichtet werden. Auch an die Rechentechnik werden bei diesem Verfahren erhebliche Anforderungen gestellt. So muss das verwendete Programmsystem in der Lage sein, eine Verzweigungsanalyse für jede Laststufe der nichtlinearen Berechnung durchzuführen, um gegebenenfalls ein "Springen" vom unterkritischen Vorbeulpfad in den überkritischen Nachbeulpfad aufzudecken.
Dieses Konzept soll hier nicht weiter erläutert werden, da es nach Meinung des Verfassers kaum Bedeutung für die Bemessungspraxis hat. Es sei aber auf den Artikel von Herbert Schmidt [2] im Stahlbau-Kalender 2012 verwiesen, der einen guten Überblick zu Schwierigkeiten beim Nachweis mittels GMNIA-Konzept gibt.
Beispiel eines Beulsicherheitsnachweis mittels MNA/LBA-Konzept
Eingabe des statischen Systems
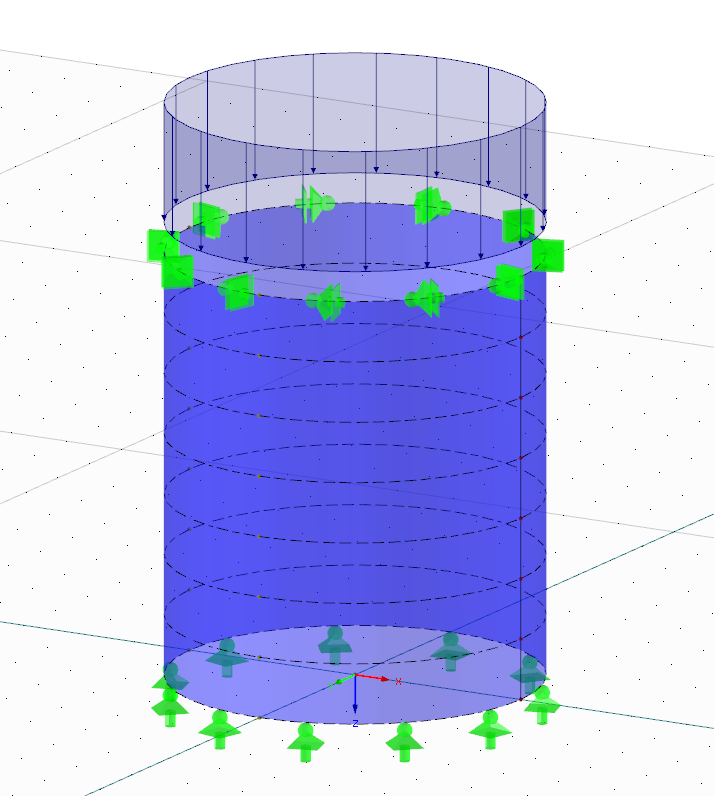
Es soll die in Bild 01 dargestellte stählerne Schale für Beulen bemessen werden. Grundsätzlich handelt es sich bei diesem Tragwerk um einen typischen Fall, bei dem ein mit der Bemessung von Stahlschalen vertrauter Ingenieur wohl kaum eine FE-Analyse in Betracht ziehen würde. Da es das Hauptziel dieses Beitrages ist, dem Leser die Thematik des Beulsicherheitsnachweises nach dem MNA/LBA-Konzept näherzubringen, soll ein möglichst einfaches Beispiel verwendet werden.
Ein wichtiges Thema bei nichtlinearen Berechnungen beziehungsweise bei Verzweigungsanalysen von Schalentragwerken ist die Elementgröße, da ungünstig gewählte FE-Netzeinstellungen zu verfälschten Ergebnissen führen können. In der Fachliteratur existieren hierfür auch diverse Überschlagsformeln, wobei das wohl sinnvollste Vorgehen eine (kleine) Konvergenzstudie darstellt.
Berechnung mit Hilfe von RFEM
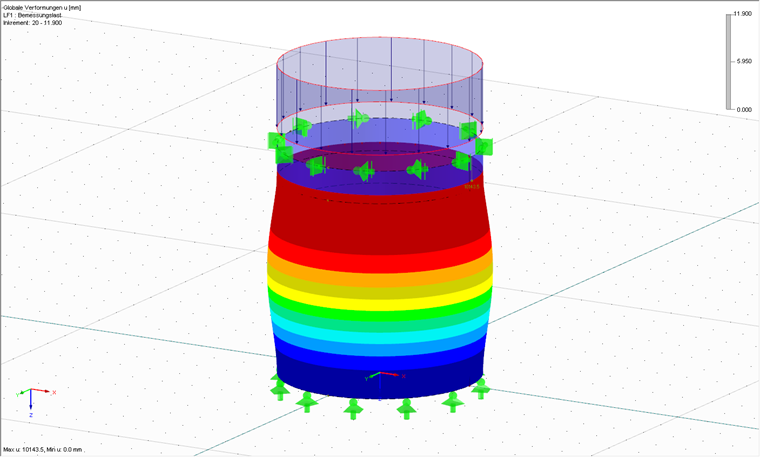
Nach der Modell- und Lasteneingabe sowie der Festlegung von geeigneten FE-Netzeinstellungen kann die Berechnung mit Hilfe von RFEM beginnen. Zunächst wird die materiell nichtlineare Analyse durchgeführt. Ziel dieser Untersuchung ist der plastische Referenzwiderstand, also derjenige Laststeigerungsfaktor, bei dem die ganze Schale plastisch versagen würde. Hierzu ist idealerweise das Zusatzmodul RF-MAT NL erforderlich, da nur so in RFEM nichtlineare Materialeigenschaften verfügbar sind. Alternativ kann auch eine linear-elastische Berechnung erfolgen und anschließend mit Formel (8.24) aus [3] der plastische Referenzwiderstand näherungsweise errechnet werden. Bild 02 zeigt den Verformungszustand nach Erreichen des plastischen Referenzwiderstandes rRpl = 11,90.
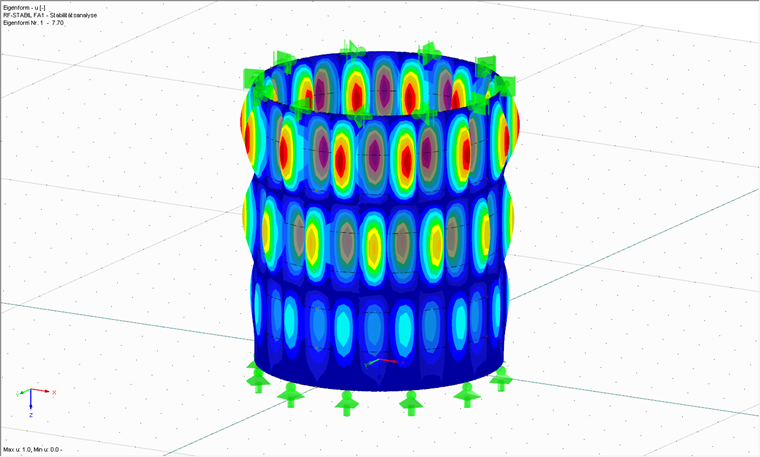
Anschließend wird die lineare Verzweigungsanalyse durchgeführt, wobei die Reihenfolge hier willkürlich gewählt wurde. Man kann auch zunächst diese Analyse vorziehen und anschließend mit der MNA fortfahren. Das Ziel der linearen Verzeigungsanalyse ist ebenfalls der Erhalt eines Laststeigerungsfaktors, jedoch diesmal derjenige, bei dem die perfekte Schale beulen würde. Hierzu ist das Zusatzmodul RF-STABIL erforderlich, mit dem lineare Verzweigungsanalysen und geometrisch nichtlineare Berechnungen durchgeführt werden können. Hiermit sind keine GMNIA-Berechnungen gemeint. Bild 03 zeigt die erste Eigenform der betrachteten Schale für den Eigenwert von rRcr = 7,70.
Beulsicherheitsnachweis
Der Beulsicherheitsnachweis ist als Ganzes im Nachfolgenden dargestellt. Besonderes Augenmerk ist dabei den vier voneinander unabhängigen Beulparametern zu widmen, welche für die meisten baupraktischen Fälle nach Anhang D in [3] ermittelt werden können.
Plastischer Referenzwiderstand aus der MNA:
rRpl = 11,9
Verzweigungslastfaktor aus der LBA:
rRcr = 7,70
Bezogener Schalenschlankheitsgrad:
Elastischer Imperfektionsfaktor:
Plastischer Bereichsfaktor:
βov = 0,60
Beulkurvenexponent:
ηov = 0,60
Vollplastischer Grenzschlankheitsgrad:
Teilplastische Grenzschlankheit:
Beul-Abminderungsfaktor:
Beulnachweis:
Das Hauptproblem der Nachweisführung ist das Einordnen der vom Programm erhaltenen Ergebnisse in einen der klassischen Beulfälle. In dem hier vorliegenden Fall ist die Sache durch die Belastung sehr einfach: Es handelt sich um quasi reines Meridiandruckbeulen. Somit errechnen sich die unabhängigen Beulparameter nach Anhang D 1.2 in der EN 1993-1-6 [3].
Das Ergebnis des Beulsicherheitsnachweises nach dem MNA/LBA-Konzept ist ein Laststeigerungsfaktor. Im hier betrachteten Beispiel beträgt er 1,515. Das heißt: Die Belastung der Schale könnte noch um über 50 % gesteigert werden.
Führt man den Nachweis mit dem spannungsbasierten Konzept, so würde sich für den hier vorliegenden Fall ein Laststeigerungsfaktor von 1,398 ergeben, was eben zeigt, dass für die klassischen Beulfälle wie das hier betrachtete Meridiandruckbeulen keine besonderen Zugewinne durch den numerisch gestützten Beulsicherheitsnachweis nach dem MNA/LBA-Konzept erzielt werden. Es sei an dieser Stelle jedoch nochmals erwähnt, dass sich dies anders verhält, sobald lokale Lasteinleitungen oder Stützungen zu Spannungskonzentrationen führen.
Fazit
Moderne, leistungsstarke und dabei anwenderfreundliche FEM-Programme wie RFEM erleichtern die Arbeit eines berechnenden Ingenieurs beim Nachweis der ausreichenden Beulsicherheit einer Schale zum Teil enorm. Durch die konsequentere Anwendung der Rechentechnik beim MNA/LBA-Konzept können in der Regel auch realistischere und dadurch meist wirtschaftlichere Ergebnisse erzielt werden.
Es sei außerdem erwähnt, dass nicht für jedes Schalentragwerk eine FE-Analyse sinnvoll ist, da für klassische Beulfälle gute analytische Verfahren zur Verfügung stehen, die zu einem geringen Dokumentationsaufwand und gleichzeitig zu ähnlich wirtschaftlichen Ergebnissen führen können. Trifft man in der Bemessungspraxis jedoch auf Fälle, die sich nicht einem klassischen Beulfall zuordnen lassen, so ist eine FE-Analyse nach dem MNA/LBA-Konzept durch RFEM mit den Zusatzmodulen RF-STABIL und RF-MAT NL eine echte Alternative zu den klassischen Verfahren.