Il est ici recommandé de ne pas simplement créer un modèle EF pour chaque coque en acier, insérer les charges et lancer le calcul. Cette procédure augmente généralement la charge de travail de l'ingénieur car plusieurs méthodes analytiques existent pour la vérification des cas simples et courants. Ces méthodes analytiques, c'est-à-dire des formules de calcul manuelles, ont également l’avantage de ne pas requérir de moyens matériels conséquents et de fournir une documentation simple. Il est même possible d'effectuer l’analyse du flambement des plaques de nombreux réservoirs sur une simple page A4. Il est impossible de produire une note de calcul aussi courte dans le cas d'un calcul aux éléments finis.
Le calcul aux éléments finis reste cependant plus judicieux dans de nombreux cas et doit être préféré à un calcul manuel. Le calcul aux éléments finis s'avère par exemple plus avantageux dans les cas suivants :
La suite de cet article détaille l’analyse du flambement d’un réservoir en acier dans RFEM conformément à l'analyse MNA/LBA. Un comportement de matériau non linéaire est ainsi appliqué.
Analyse du flambement des plaques selon l'EN 1993-1-6
L'EN 1993-1-6 présente trois méthodes pour l'analyse du flambement des coques en acier. Elles sont brièvement présentées et analysés ci-dessous en fonction des exigences informatiques et de planification.
Analyse du flambement des plaques par la méthode des contraintes
Il s'agit de la méthode d’analyse de base utilisée par tous les ingénieurs ayant déjà effectué des vérifications de coques. Un ingénieur qualifié peut facilement appliquer cette méthode, qui requiert une puissance de calcul très réduite voire inexistante grâce aux calculs manuels fréquemment utilisés dans ce cas.
Il est toutefois difficile d'obtenir des résultats économiques avec cette méthode pour les structures à coque présentant des situations de charge très différentes des formes de flambement les plus courantes. Cette méthode peut en outre laisser penser à tort que la résistance au flambement de la structure en coque dépend uniquement des contraintes qui s'exercent. Si tel était le cas, il ne serait pas utile de renforcer la paroi de la coque (à l'aide de nervures longitudinales, par exemple) car les contraintes n'en seraient pas réduites de manière significative. La résistance au flambement d'une coque correctement raidie est cependant bien plus élevée que celle d'une coque non raidie avec une paroi de même épaisseur.
Analyse numérique globale du flambement des plaques MNA/LBA
Cette méthode doit être utilisée pour la vérification de la coque de l'exemple traité dans cet article. L'analyse MNA/LBA requiert plus de connaissances sur la stabilité des coques que la méthode selon la méthode basée sur les contraintes. Cette méthode nécessite un matériel dont les performances de calcul sont plus élevées car une analyse linéaire élastique des bifurcations (LBA) et un analyse matériellement non linéaire (MNA) doivent être effectuées.
Cette méthode constitue le type d'analyse du flambement de plaque le plus judicieux pour les calculs à l'aide d'une analyse aux éléments finis. L'analyse MNA/LBA permet en effet de réaliser la majeure partie de cette vérification sur ordinateur sans solliciter fortement un ingénieur. Le calcul élastique linéaire des efforts internes de la coque en vue de l'analyse par la méthode des contraintes s'avèrerait trop incohérent d'un point de vue informatique, car des logiciels puissants tels que RFEM peuvent également déterminer la résistance de la structure de coque.
Analyse numérique globale du flambement des plaques GMNIA
L'analyse géométriquement et matériellement non linéaire incluant les imperfections (GMNIA) pour déterminer une stabilité de coque suffisante est probablement la méthode la plus cohérente pour analyser le flambement de plaque. Les efforts internes sont alors calculés géométriquement et matériellement de manière non linéaire à l'aide des imperfections.
Cette méthode requiert des connaissances approfondies sur la stabilité des coques, car il est très difficile d'appliquer correctement les imperfections (comportement de pré-flambement). Sinon, il est recommandé de ne pas effectuer de vérification selon l'analyse GMNIA. Cette méthode nécessite également des performances informatiques très élevées. L’ordinateur et le logiciel utilisés doivent donc être capable d'effectuer une analyse de stabilité pour chaque incrément de charge du calcul non linéaire pour détecter d'éventuelles bifurcations dans le trajet de chargement entre le pré-flambement subcritique et le post-flambement supercritique, le cas échéant.
Cette méthode ne sera pas détaillée ici, car le présent article n'est pas consacré à ce cas précis de calcul. L’article d'Herbert Schmidt [2] publié dans le Stahlbau-Kalender de 2012 (en allemand) donne néanmoins un bon aperçu des difficultés rencontrées lors de la vérification selon l'analyse GMNIA.
Exemple d'analyse du flambement des plaques selon l'analyse MNA/LBA
Entrée du système structural
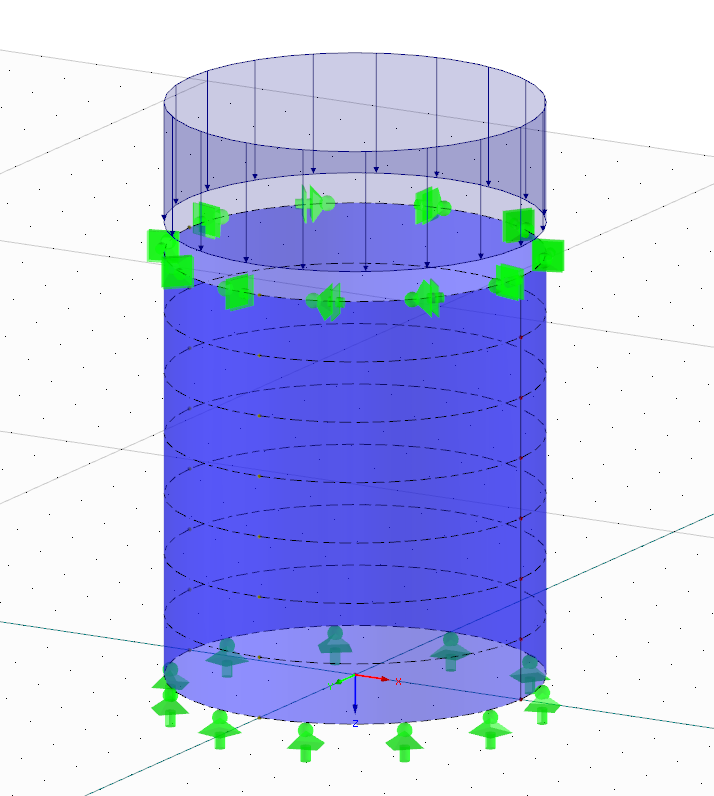
Une analyse du flambement doit être effectuée pour la coque en acier illustrée par la Figure 01. Cette structure constitue un cas type pour lequel un ingénieur familiarisé avec la vérification des coques en acier n'envisagerait vraisemblablement pas d'effectuer une analyse aux éléments finis. L'objectif principal de cet article étant d'expliquer l'analyse du flambement des plaques selon l'analyse MNA/LBA, l'exemple le plus simple est utilisé ci-dessous.
La taille des éléments constitue un paramètre important des calculs non linéaires lors des analyses de stabilité des structures en coque car un maillage EF paramétré de manière incorrecte peut mener à des résultats erronés. Diverses formules générales préconisant une (brève) analyse de la convergence sont également disponibles dans la littérature spécialisée.
Calcul à l'aide de RFEM
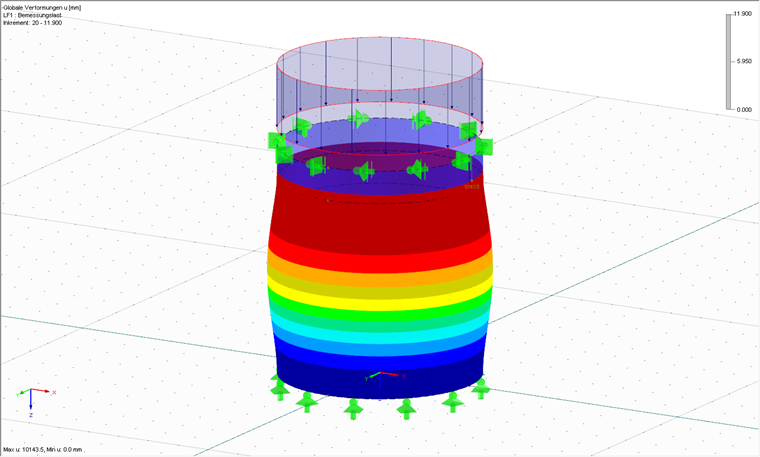
Une fois le modèle ainsi que la charge entrés et les paramètres de maillage EF adéquats définis, le calcul peut être lancé à l'aide de RFEM. Une analyse matériellement non linéaire est tout d'abord effectuée. L'objectif est de déterminer la résistance de référence plastique, c'est-à-dire le facteur d'incrémentation de charge entraînant l'effondrement plastique de la coque entière. Il est conseillé d'utiliser le module additionnel RF-MAT NL car seules des propriétés de matériau non linéaires sont disponibles dans RFEM. Une autre méthode consisterait à effectuer un calcul linéaire élastique, puis à calculer approximativement cette résistance de référence à l'aide de la formule (8.24) de [3]. La Figure 02 montre l'état de la structure déformée après avoir atteint la résistance de référence plastique rRpl = 11,90.
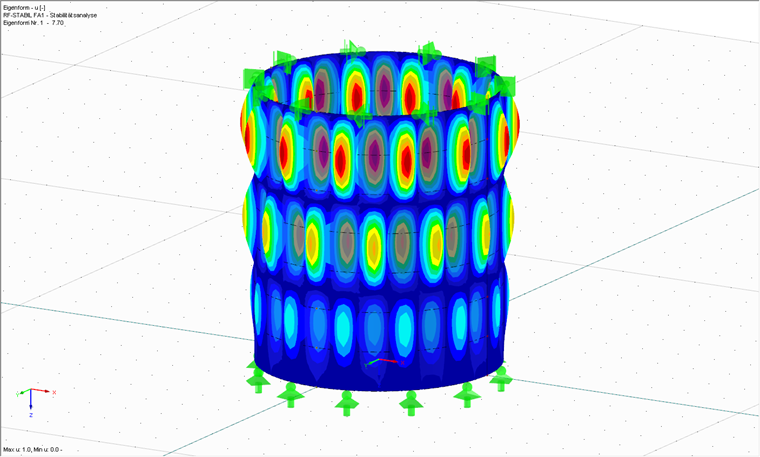
On effectue ensuite l'analyse de stabilité selon un ordre choisi arbitrairement. Il est également possible d'effectuer d'abord cette analyse de stabilité, puis de poursuivre avec l’analyse ANM. Le but de cette analyse est également d'obtenir un facteur d'incrément de charge qui provoquerait le flambement d'une coque parfaite. Le module additionnel RF-STABILITY vous permet d'effectuer des analyses de stabilité linéaires et des calculs géométriques non linéaires. Il ne s'agit donc pas ici de calcul selon l'analyse GMNIA. La Figure 03 montre le premier mode propre la coque considérée avec une valeur propre de rRcr = 7,70.
Analyse du flambement des plaques
Cette analyse est présentée dans son ensemble ci-dessous. Une attention particulière doit être prêtée aux quatre paramètres de flambement indépendants, qui peuvent être déterminés selon l’Annexe D de [3] pour la plupart des cas.
Résistance de référence plastique selon l'analyse MNA :
rRpl = 11,9
Facteur de charge critique selon l'analyse LBA :
rRcr = 7,70
Élancement réduit global pour la structure entière :
Facteur d'imperfection élastique :
Facteur de domaine plastique :
βov = 0,60
Exposant d'interaction pour le flambement :
ηov = 0,60
Élancement réduit à la limite d'affaissement :
Élancement réduit à la limite plastique :
Élancement réduit global :
Analyse du flambement :
La classification des résultats obtenus par le logiciel dans l'un des cas de flambement classiques constitue le problème principal pour ce calcul. Le chargement de cet exemple est un cas très simple car il s’agit quasiment d'un flambement par compression méridienne. Les paramètres de flambement indépendants sont calculés selon l'Annexe D 1.2 de l'EN 1993-1-6 [3].
Au terme de l'analyse du flambement selon l'analyse MNA/LBA, on obtient un facteur d'incrément de charge. Dans l'exemple traité dans cet article, ce facteur est de 1,515, Cela signifie que : la charge sur la coque peut être augmentée de plus de 50 %.
Si l'analyse est effectuée selon la méthode des contraintes, on obtiendrait un facteur d'incrément de charge de 1,398, ce qui montre que l'analyse MNA/LBA ne présenterait aucun avantage particulier pour les cas de flambement classiques tels que la compression méridienne considérée ici. Ce n'est cependant pas le cas dès que les charge locales entrées ou les appuis provoquent des concentrations de contraintes.
Résumé
Des logiciels d'analyse aux éléments finis modernes, puissants et conviviaux tels que RFEM facilitent considérablement le travail des calculateurs concernant la résistance au flambement des coques. Il est généralement possible d'obtenir des résultats plus réalistes et donc plus économiques grâce aux analyses ANM/LBA informatisées.
Il convient également de noter que les analyses EF ne sont pas pertinentes pour toutes les structures en coques car des méthodes analytiques efficaces s'accompagnant d'une documentation réduite et fournissant des résultats tout aussi économiques existent également pour les cas de flambement classiques. Une analyse aux éléments finis selon l'analyse MNA/LBA effectuée à l'aide RFEM ainsi que des modules additionnels RF-STABILITY et RF-MAT NL constitue une alternative efficace aux méthodes classiques si le cas de flambement traité ne se prête pas à celles-ci.