В этой статье мы также настоятельно рекомендуем не просто создавать одну КЭ-модель для каждой стальной оболочки, настраивать нагрузки и затем нажимать «Рассчитать». В большинстве случаев эта процедура требует дополнительной работы, поскольку для простых случаев, которые распространены в практике проектирования, доступны многочисленные аналитические методы проверки. Эти аналитические методы, формулы ручного расчета, также имеют большое преимущество в виде экономии места и простоты документирования. Для некоторых контейнеров анализ потери устойчивости пластин можно выполнить на странице формата А4. Такая компактная документация невозможна при анализе КЭ.
Однако есть также множество случаев, когда использование метода конечных элементов имеет смысл и его следует предпочесть ручному расчету. Следующие пункты являются лишь несколькими примерами случаев, когда имеет смысл использовать расчет КЭ:
В следующем тексте расчет потери устойчивости стальной оболочки выполняется с помощью программы RFEM в соответствии с концепцией MNA/LBA. Таким образом, применяется нелинейное поведение материала стали.
Расчет на изгиб пластин в соответствии с EN 1993-1-6
В стандарте EN 1993-1-6 представлены три варианта выполнения расчета потери устойчивости стальных оболочек. В этом разделе они должны быть кратко перечислены и оценены с учетом требований вычислительной техники, а также требований, предъявляемых к инженеру-проектировщику.
Расчет потери устойчивости пластин на основе напряжений
Расчет потери устойчивости пластин на основе напряжений считается стандартным методом расчета, который использует почти каждый инженер при проектировании оболочки. Опытный инженер классифицирует этот метод как простой, а требования к вычислениям либо очень низкие, либо отсутствуют, поскольку часто используются формулы для ручного расчета.
Основная проблема этого метода расчета заключается в том, что экономические результаты вряд ли будут достигнуты для оболочечных конструкций с условиями нагружения, которые значительно отличаются от стандартных режимов потери устойчивости. Вдобавок, как пользователь этой концепции, вы ошибаетесь этим методом, потому что легко можете подумать, что устойчивость пластин каркаса к потере устойчивости зависит только от возникающих напряжений. Если бы это было так, то усиление стенки оболочки, например, продольными ребрами не принесло бы пользы, так как это не приводит к значительному снижению напряжений. На самом деле, устойчивость плиты к изгибу искусно усиленной оболочки намного выше, чем у несвязанной оболочки той же толщины стенки.
Расчет потери устойчивости плиты на основе численного расчета с помощью глобального расчета MNA/LBA
Этот метод будет использован для следующей конструкции оболочки. Расчет MNA/LBA, безусловно, требует, чтобы пользователь имел несколько больше базовых знаний в области устойчивости оболочки, чем в случае метода расчета на основе напряжений. Кроме того, вычислительная техника должна быть более мощной, поскольку для правильного применения этого метода необходимо выполнить линейный упругий бифуркационный анализ (LBA) и нелинейный анализ материала (MNA).
По мнению автора, этот метод расчета является наиболее эффективным способом выполнения расчета потери устойчивости пластины, если расчет должен выполняться с использованием метода КЭ. Обоснование этого состоит в том, что для проекта, использующего концепцию MNA/LBA, вычислительная технология используется последовательно, не ожидая от пользователя слишком больших усилий. Если внутренние силы оболочки рассчитываются линейно-упругими, чтобы использовать их для расчета потери устойчивости пластин на основе напряжений, компьютерная технология будет использоваться слишком непоследовательно, поскольку мощные программы, такие как RFEM, также могут определить несущую способность пластины структура оболочки.
Расчет потери устойчивости пластин на основе численного расчета с помощью расчета GMNIA
Анализ GMNIA для определения достаточной устойчивости оболочки, вероятно, является наиболее последовательным методом анализа потери устойчивости пластин. Таким образом, внутренние силы рассчитываются геометрически и нелинейно по материалам с учетом несовершенств.
Этот метод требует от пользователя отличных предварительных знаний об устойчивости оболочки, так как, помимо прочего, очень сложно правильно устранить дефекты (предварительная потеря устойчивости). Если у пользователя нет этих базовых знаний, в любом случае следует избегать процесса проектирования с использованием концепции GMNIA. Кроме того, при использовании этого метода к компьютерной технике предъявляются большие требования. Таким образом, используемая программная система должна быть способна выполнять бифуркационный анализ для каждого шага нагрузки нелинейного анализа, чтобы, при необходимости, обнаруживать «скачок» от докритической траектории до потери устойчивости к сверхкритической траектории после потери устойчивости.
Эта концепция не будет здесь объяснена, поскольку, по мнению автора, она не имеет большого значения для практики проектирования. Для получения дополнительной информации, пожалуйста, обратитесь к статье Герберта Шмидта [2] в календаре стальных конструкций на 2012 год, в которой дается хороший обзор трудностей, возникающих при использовании расчета по методу GMNIA.
Пример анализа потери устойчивости пластины с использованием метода MNA/LBA
Ввод конструктивной системы
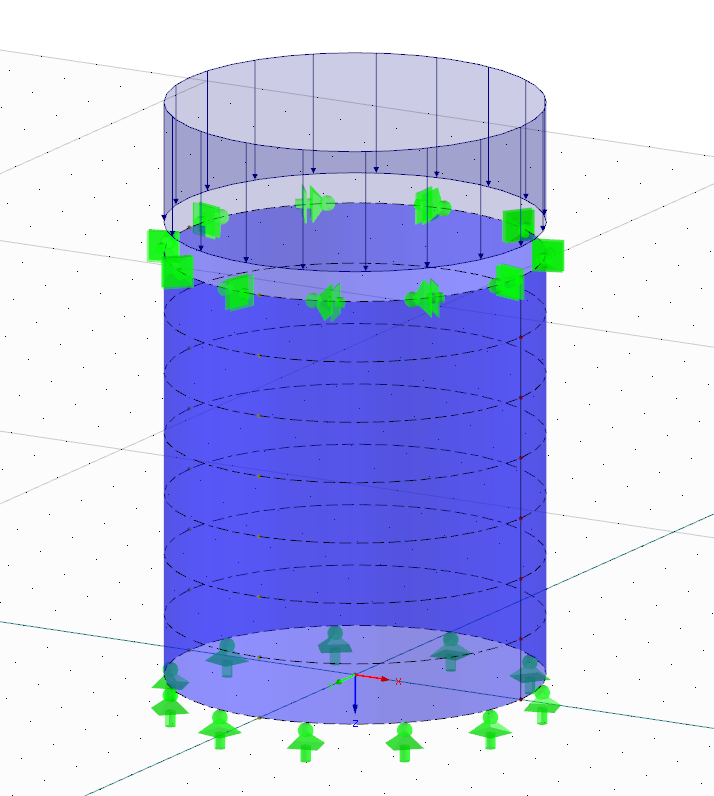
Стальная оболочка, показанная на рисунке 01, будет рассчитана на изгиб. В принципе, эта конструкция является типичным случаем, когда инженер, знакомый с конструкцией стальных оболочек, вряд ли станет рассматривать КЭ анализ. Поскольку основная цель данной статьи - познакомить читателя с темой анализа потери устойчивости пластин в соответствии с концепцией MNA/LBA, будет использован максимально простой пример.
Важной темой в нелинейных расчетах или расчете бифуркаций оболочек является размер элемента, поскольку неудачно выбранные параметры сетки КЭ могут привести к фальсификации результатов. В специальной литературе для этого существуют различные формулы для грубого расчета, где исследование (малой) сходимости является наиболее подходящим подходом.
Расчет с помощью RFEM
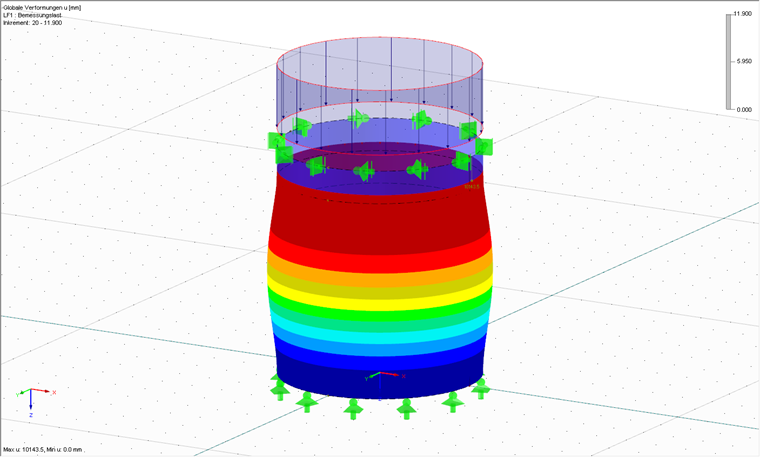
После ввода модели и нагрузки и выбора подходящих настроек сетки КЭ можно начинать расчет с помощью RFEM. Сначала выполняется нелинейный анализ материала. Целью этого анализа является эталонное пластическое сопротивление (то есть критический коэффициент нагрузки, при котором вся оболочка разрушится пластически). Дополнительный модуль RF-MAT NL идеально подходит для использования, так как тогда в RFEM доступны только нелинейные свойства материала. В качестве альтернативы можно выполнить линейный расчет упругости; Тогда пластическое эталонное сопротивление можно приблизительно рассчитать по формуле (8.24) из [3]. На рис. 02 показана деформированная система после достижения эталонного пластического сопротивления rRpl = 11,90.
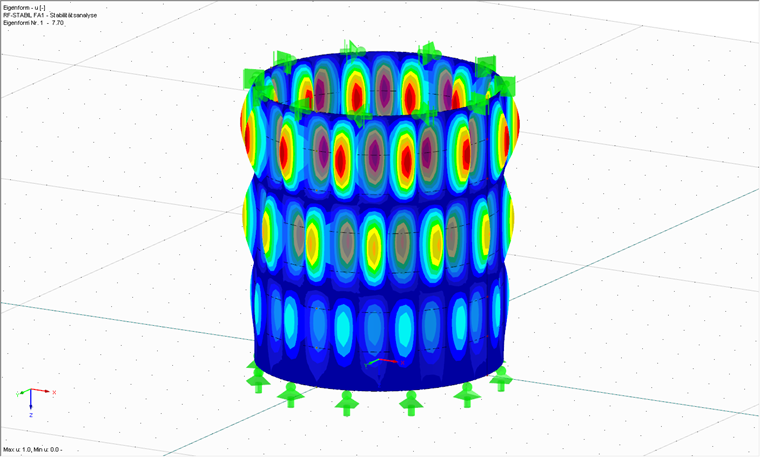
Затем выполняется линейный бифуркационный анализ, в котором последовательность была выбрана произвольно. Также возможно сначала выполнить этот анализ, а затем продолжить с помощью метода MNA. Целью линейного бифуркационного анализа также является получение критического коэффициента нагрузки, но на этот раз такого, который приведет к потере устойчивости идеальной оболочки. Для этого требуется дополнительный модуль RF-STABILITY, с помощью которого можно выполнять линейный бифуркационный анализ и геометрически нелинейные расчеты. Это не относится к расчетам GMNIA. На рисунке 03 показана форма первой моды рассматриваемой оболочки для собственного значения rRcr = 7,70.
Расчет пластин на потерю устойчивости
В следующем тексте весь анализ потери устойчивости показан в целом. Особое внимание следует уделить четырем независимым параметрам потери устойчивости, которые могут быть определены для большинства практических случаев строительства в соответствии с приложением D в [3].
Пластическое эталонное сопротивление из MNA:
rRpl = 11,9
Коэффициент критической нагрузки от LBA:
rRcr = 7,70
Степень гибкости:
Коэффициент упругого несовершенства:
Пластический коэффициент умножения:
βов = 0,60
Показатель кривой потери устойчивости:
ηов = 0,60
Полностью пластичная, предельная степень гибкости:
Частично пластичная, ограничивающая стройность:
Коэффициент уменьшения потери устойчивости:
Расчет на изгиб пластин:
Основной задачей расчета является отнесение результатов, полученных с помощью программы, к одному из типичных случаев потери устойчивости. В данном случае это очень просто из-за нагрузки: Речь идет о потере устойчивости при меридиональном давлении. Таким образом, рассчитываются независимые параметры потери устойчивости согласно приложению D 1.2 в EN 1993-1-6 [3].
Результатом расчета потери устойчивости пластины по методу MNA/LBA является критический коэффициент нагрузки. В показанном здесь примере это 1,515. Это означает: Нагрузку на снаряд можно было увеличить более чем на 50%.
Если анализ основан на концепции, основанной на напряжениях, это приведет к коэффициенту критической нагрузки 1,398, который показывает, что для типичных случаев потери устойчивости, таких как рассматриваемая здесь потеря устойчивости при меридиональном давлении, использование пластины, основанной на численных значениях, не дает дополнительных преимуществ. Расчет потери устойчивости по методу MNA/LBA. Следует отметить, как уже упоминалось, что это отличается, если местные нагрузки или опоры приводят к концентрациям напряжений.
Заключение
Современные, мощные и удобные в использовании программы МКЭ, такие как RFEM, значительно облегчают работу инженеров-расчетчиков при выполнении расчетов, обеспечивающих достаточную устойчивость оболочки к потере устойчивости. В результате более последовательного использования компьютерных технологий в концепции MN/LBA, как правило, могут быть достигнуты более реалистичные и, следовательно, более экономичные результаты.
Следует также отметить, что анализ КЭ не рекомендуется для каждой конструкции оболочки, поскольку для типичных случаев потери устойчивости доступны хорошие аналитические методы, которые могут привести к сокращению документации и таким же экономическим результатам. Однако, если в процессе проектирования инженер сталкивается со случаями, которые не могут быть отнесены к типичному случаю потери устойчивости, анализ КЭ по концепции MNA/LBA с помощью RFEM с дополнительными модулями RF-STABILITY и RF-MAT NL является реальной задачей. альтернатива стандартным методам.