Cálculo de paredes em painéis de madeira | 2. Rigidez e flexibilidade de uma parede

O cálculo da deformação refere-se ao primeiro artigo desta série.

• KB | Cálculo de paredes de painéis de madeira | 1.º Determinação da capacidade de carga e rigidez

1 Sistema estrutural

Rigidez de uma parede

A rigidez de uma parede é calculada sob uma carga unitária de 1 kN. Informações adicionais sobre as equações utilizadas podem ser encontradas na literatura referenciada [1] assim como no artigo anterior mencionado acima.

Exemplo

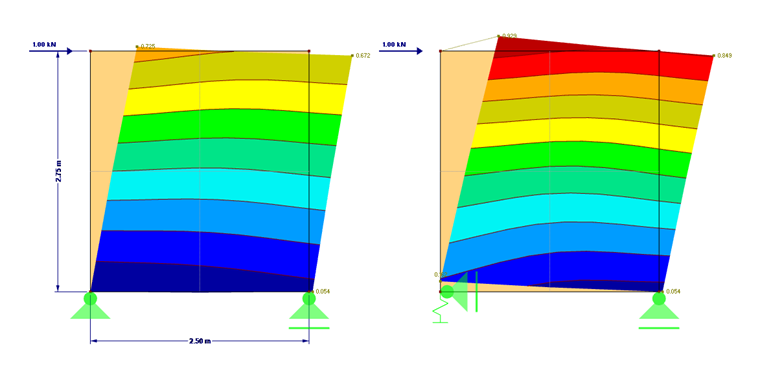
O cálculo da rigidez é realizado para um exemplo simples com as dimensões mostradas na Imagem 01.

2 Sistema estrutural

Sistema

• Comprimento da parede l = 2,50 m
• Altura da parede h = 2,75 m
• Poste C24 6/12 cm, ρ_m,T = 350 kg/m³
• Revestimento OSB 3, t = 18 mm (unilateral), ρ_m,O = 439 kg/m³, G = 108 kN/cm²
• k_ser = 159N/mm
• b_E = b+t = 12cm + 1,8cm = 13,8 cm
• Grampos d = 1,5 mm, t = 45 mm
• Distância entre grampos a_v = 60 mm (fila única)
• Malha 62,5 cm
• Ancoragem com 10 pregos de diâmetro 4,2 mm pregados
• Tamanho da malha FE é 1,3m (4 elementos por painel)

Rigidez

• Cedência do elemento de ligação (grampos):
  $${\mathrm{u}}_{\mathrm{k},\mathrm{inst}} = \left(2 · \mathrm{l} + 2 · \mathrm{h}\right) · \frac{{\mathrm{a}}_{\mathrm{v}}}{{\mathrm{k}}_{\mathrm{ser}} · \mathrm{l}²} · \mathrm{F}$$

  $$= \left(2 · 2500 \mathrm{mm} + 2 · 2750 \mathrm{mm}\right) · \frac{60 \mathrm{mm}}{159 \mathrm{N}/\mathrm{mm} · (2500 \mathrm{mm})²} · 1000 \mathrm{N}$$

  $$= 0.634 \mathrm{mm}$$

  Flexibilidade do ligador (grampo)
• Cedência do revestimento:
  $${\mathrm{u}}_{\mathrm{G},\mathrm{inst}} = \frac{\mathrm{F} · \mathrm{h}}{{\displaystyle \mathrm{G} · \mathrm{A}}} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm}}{{\displaystyle 1080 \mathrm{N}/\mathrm{mm}² · 18 \mathrm{mm} · 2500 \mathrm{mm}}} = 0.057 \mathrm{mm}$$

  Rigidez do revestimento
• Cedência das nervuras:
  $${\mathrm{u}}_{\mathrm{E},\mathrm{inst}} = \frac{2}{3} · \frac{\mathrm{F} · {\mathrm{h}}^3}{\mathrm{E} · \mathrm{A} · {\mathrm{l}}^2} = \frac{2}{3} · \frac{1000 \mathrm{N} ·(2750 \mathrm{mm})³}{11000 \mathrm{N}/\mathrm{mm}² · 60 \mathrm{mm} · 120 \mathrm{mm} · (2500 \mathrm{mm})²} = 0.028 \mathrm{mm}$$

  Flexibilidade das nervuras
• Cedência da âncora:
  $$\begin{array}{l}{\mathrm{k}}_{\mathrm{ser}} = 10 · {\mathrm{\rho }}_{\mathrm{m}}^{1.5} · \frac{{\mathrm{d}}^{0.8}}{30} = 10 · {(350 \mathrm{kg}/\mathrm{m}³)}^{1.5} · \frac{{(4.2 \mathrm{mm})}^{0.8}}{30} = 6879.9 \mathrm{N}/\mathrm{mm}\\ {\mathrm{u}}_{\mathrm{K},\mathrm{DF}} = \mathrm{h} · \sin \mathrm{\alpha } = 2750 \mathrm{mm} · \sin (0.0195) = 0.94 \mathrm{mm}\\ \mathrm{\alpha } = \frac{\mathrm{F} · \mathrm{h} · 180}{{\mathrm{K}}_{\mathrm{DF}} · \mathrm{\pi }} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm} · 180}{8.06 · {10}^9 · \mathrm{\pi }} = 0.0195°\\ {\mathrm{K}}_{\mathrm{DF}} = \frac{{\mathrm{l}}^2 · {\mathrm{k}}_{\mathrm{ser}}}{2} = \frac{(2500 \mathrm{mm})² · 6879.9 \mathrm{N}/\mathrm{mm}}{2} = 2.15 · {10}^{10}\end{array}$$

  Flexibilidade da âncora
• Soma das Cedências (calculado sem a âncora):
  $${\mathrm{u}}_{\mathrm{inst}} = {\mathrm{u}}_{\mathrm{E},\mathrm{inst}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{G},\mathrm{inst}}}}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{k},\mathrm{inst}}}}} = 0.028 0.07 0.63 = 0.728 \mathrm{mm}$$

  Soma de deslizamentos

Conversão em área efetiva

A rigidez calculada é convertida numa rigidez de painel ortotrópico efetivo. Leia este artigo técnico obter informação adicional sobre o modelo de material ortotrópico.

• KB | Leis de material ortotrópico

• Componente da rigidez normal:
  $$\begin{array}{l}{\mathrm{E}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}³}{{3 · \mathrm{u}}_{\mathrm{E},\mathrm{inst}} · {\displaystyle \frac{\mathrm{l}³ · \mathrm{b}}{12}}}=\frac{1 \mathrm{kN} · (275 \mathrm{cm})³}{3 · 0.0028 \mathrm{cm} · {\displaystyle \frac{(250 \mathrm{cm})³ · 12 \mathrm{cm}}{12}}} = 158.45 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}66/77 = \frac{\mathrm{E} · \mathrm{d}}{1 - \mathrm{\nu }} = 158.45 \mathrm{kN}/\mathrm{cm}² · 12 \mathrm{cm} = 1901.4 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Componente de rigidez normal
• Rigidez ao corte no plano da parede:
  $$\begin{array}{l}{\mathrm{G}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}}{({\mathrm{u}}_{\mathrm{G},\mathrm{inst}} {\mathrm{u}}_{\mathrm{k},\mathrm{inst}}) · {\displaystyle \frac{5}{6}} · {\mathrm{b}}_{\mathrm{E}} · \mathrm{l}} = \frac{1 \mathrm{kN} · 275 \mathrm{cm}}{0.07 \mathrm{cm} · {\displaystyle \frac{5}{6}} · 13.8 \mathrm{cm} · 250 \mathrm{cm}} = 1.37 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}88 = {\mathrm{G}}_{\mathrm{eq}} · {\mathrm{b}}_{\mathrm{E}} = 1.37 \mathrm{kN}/\mathrm{cm}² · 13.8 \mathrm{cm} = 18.86 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Rigidez de corte no plano da viga-parede

A âncora pode ser diretamente definida no RFEM como uma mola linear elástica com a rigidez de mola calculada de 6.879,9 N/mm. A comparação das deformações é apresentada na Imagem 1. As diferenças também podem ser observadas no Modelo 1 anexado a este artigo.

Para um cálculo tridimensional, este método apresenta o problema da definição da rigidez à flexão dos painéis. Isto é explicado de forma mais detalhada no artigo técnico mencionado acima sobre modelos de materiais ortotrópicos.

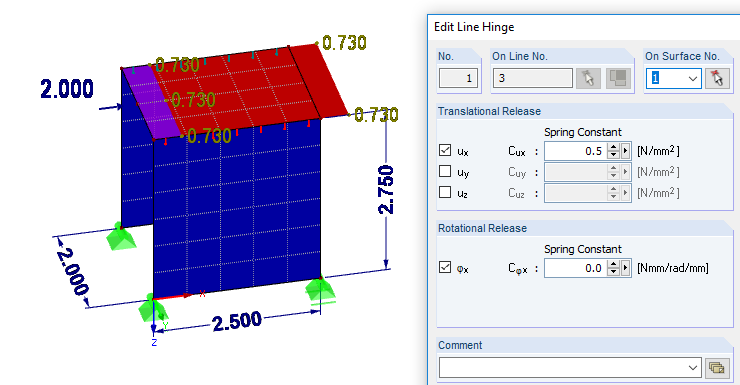
Em vez de representar a rigidez da parede em painéis de madeira através de superfícies, é apresentado abaixo um método para converter a cedência calculada numa libertação de linha.

3 Modelo espacial

A vantagem é que as propriedades de superfície do modelo podem ser assumidas como rígidas.

Conclusão

Neste artigo foi apresentado o cálculo de um painel em madeira utilizando de uma superfície ortotrópica efetiva. A âncora pode ser definida diretamente como rigidez de mola. Para um cálculo linear bidimensional do sistema, os resultados coincidem com os cálculos manuais em [1]. Assim, pode ser realizado um dimensionamento real com as cargas de um cálculo de contraventamento. O modelo para o cálculo de exemplo está disponível em downloads.

Outra opção seria a conversão da cedência numa mola linear de linha. Para modelos espaciais, este método é o mais adequado, pois exclui em grande parte a influência da flexão do painel e da flexão no plano do painel. O modelo também se encontra disponível em downloads.

O próximo artigo irá apresentar a rigidez de um piso em 2D bem como o dimensionamento dos painéis de parede em 3D.