Cálculo de muros de paneles de madera | 2. Rigidez y deslizamiento de un muro

El cálculo de la deformación se refiere al primer artículo de esta serie.

• Kb | Cálculo de muros de paneles de madera | 1. Determinación de la capacidad de carga y rigidez

1 Sistema estructural

Rigidez de una pared

La rigidez de una pared se calcula bajo una carga unitaria de 1 kN. Se puede encontrar información adicional sobre las ecuaciones utilizadas aquí en la literatura mencionada [1] así como en el artículo previo mencionado de esta serie.

Ejemplo

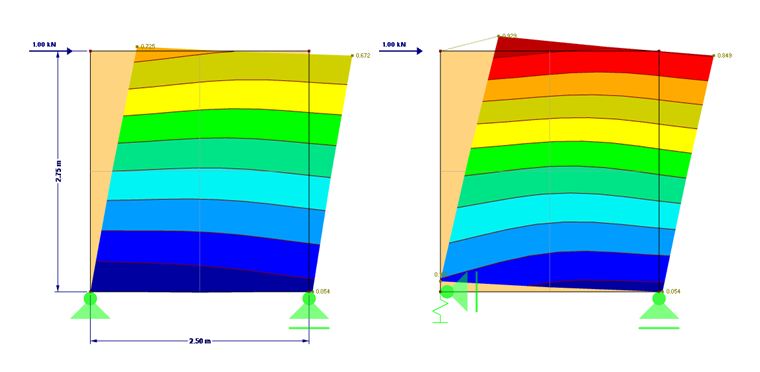
El cálculo de la rigidez se realiza para un ejemplo sencillo con las dimensiones mostradas en la Imagen 01.

2 Sistema estructural

Sistema

• Longitud de la pared l = 2,50 m
• Altura de la pared h = 2,75 m
• Montantes C24 6/12 cm, ρ_m,T = 350 kg/m³
• Revestimiento OSB 3, t = 18 mm (unilateral), ρ_m,O = 439 kg/m³, G = 108 kN/cm²
• k_ser = 159N/mm
• b_E = b+t = 12cm + 1,8cm = 13,8 cm
• Grapado d = 1,5 mm, t = 45 mm
• Distancia de grapado a_v = 60 mm (una fila)
• Cuadrícula de 62,5 cm
• Anclaje de tracción con 10 clavos de diámetro 4,2 mm clavados
• Tamaño de la malla FE es de 1,3m (4 elementos por panel)

Rigidez

• Deformabilidad del conector (grapa):
  $${\mathrm{u}}_{\mathrm{k},\mathrm{inst}} = \left(2 · \mathrm{l} + 2 · \mathrm{h}\right) · \frac{{\mathrm{a}}_{\mathrm{v}}}{{\mathrm{k}}_{\mathrm{ser}} · \mathrm{l}²} · \mathrm{F}$$

  $$= \left(2 · 2500 \mathrm{mm} + 2 · 2750 \mathrm{mm}\right) · \frac{60 \mathrm{mm}}{159 \mathrm{N}/\mathrm{mm} · (2500 \mathrm{mm})²} · 1000 \mathrm{N}$$

  $$= 0.634 \mathrm{mm}$$

  Fluencia del medio de fijación (sujeción)
• Deformabilidad del revestimiento:
  $${\mathrm{u}}_{\mathrm{G},\mathrm{inst}} = \frac{\mathrm{F} · \mathrm{h}}{{\displaystyle \mathrm{G} · \mathrm{A}}} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm}}{{\displaystyle 1080 \mathrm{N}/\mathrm{mm}² · 18 \mathrm{mm} · 2500 \mathrm{mm}}} = 0.057 \mathrm{mm}$$

  Rigidez de Revestimiento
• Deformabilidad de los nervios:
  $${\mathrm{u}}_{\mathrm{E},\mathrm{inst}} = \frac{2}{3} · \frac{\mathrm{F} · {\mathrm{h}}^3}{\mathrm{E} · \mathrm{A} · {\mathrm{l}}^2} = \frac{2}{3} · \frac{1000 \mathrm{N} ·(2750 \mathrm{mm})³}{11000 \mathrm{N}/\mathrm{mm}² · 60 \mathrm{mm} · 120 \mathrm{mm} · (2500 \mathrm{mm})²} = 0.028 \mathrm{mm}$$

  Fluencia de los nervios
• Deformabilidad del anclaje:
  $$\begin{array}{l}{\mathrm{k}}_{\mathrm{ser}} = 10 · {\mathrm{\rho }}_{\mathrm{m}}^{1.5} · \frac{{\mathrm{d}}^{0.8}}{30} = 10 · {(350 \mathrm{kg}/\mathrm{m}³)}^{1.5} · \frac{{(4.2 \mathrm{mm})}^{0.8}}{30} = 6879.9 \mathrm{N}/\mathrm{mm}\\ {\mathrm{u}}_{\mathrm{K},\mathrm{DF}} = \mathrm{h} · \sin \mathrm{\alpha } = 2750 \mathrm{mm} · \sin (0.0195) = 0.94 \mathrm{mm}\\ \mathrm{\alpha } = \frac{\mathrm{F} · \mathrm{h} · 180}{{\mathrm{K}}_{\mathrm{DF}} · \mathrm{\pi }} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm} · 180}{8.06 · {10}^9 · \mathrm{\pi }} = 0.0195°\\ {\mathrm{K}}_{\mathrm{DF}} = \frac{{\mathrm{l}}^2 · {\mathrm{k}}_{\mathrm{ser}}}{2} = \frac{(2500 \mathrm{mm})² · 6879.9 \mathrm{N}/\mathrm{mm}}{2} = 2.15 · {10}^{10}\end{array}$$

  Fluencia del anclaje
• Suma de las deformabilidades (calculada sin anclaje de tracción):
  $${\mathrm{u}}_{\mathrm{inst}} = {\mathrm{u}}_{\mathrm{E},\mathrm{inst}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{G},\mathrm{inst}}}}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{k},\mathrm{inst}}}}} = 0.028 0.07 0.63 = 0.728 \mathrm{mm}$$

  Suma de deslizamientos

Conversión a área efectiva

La rigidez calculada se convierte en una rigidez de panel ortotrópica efectiva. La información de fondo sobre el modelo de material ortotrópico se encuentra en este artículo técnico.

• Kb | Leyes de los materiales ortótropos

• Componente de rigidez normal:
  $$\begin{array}{l}{\mathrm{E}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}³}{{3 · \mathrm{u}}_{\mathrm{E},\mathrm{inst}} · {\displaystyle \frac{\mathrm{l}³ · \mathrm{b}}{12}}}=\frac{1 \mathrm{kN} · (275 \mathrm{cm})³}{3 · 0.0028 \mathrm{cm} · {\displaystyle \frac{(250 \mathrm{cm})³ · 12 \mathrm{cm}}{12}}} = 158.45 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}66/77 = \frac{\mathrm{E} · \mathrm{d}}{1 - \mathrm{\nu }} = 158.45 \mathrm{kN}/\mathrm{cm}² · 12 \mathrm{cm} = 1901.4 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Componente de rigidez normal
• Rigidez al cortante en el plano del panel:
  $$\begin{array}{l}{\mathrm{G}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}}{({\mathrm{u}}_{\mathrm{G},\mathrm{inst}} {\mathrm{u}}_{\mathrm{k},\mathrm{inst}}) · {\displaystyle \frac{5}{6}} · {\mathrm{b}}_{\mathrm{E}} · \mathrm{l}} = \frac{1 \mathrm{kN} · 275 \mathrm{cm}}{0.07 \mathrm{cm} · {\displaystyle \frac{5}{6}} · 13.8 \mathrm{cm} · 250 \mathrm{cm}} = 1.37 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}88 = {\mathrm{G}}_{\mathrm{eq}} · {\mathrm{b}}_{\mathrm{E}} = 1.37 \mathrm{kN}/\mathrm{cm}² · 13.8 \mathrm{cm} = 18.86 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Rigidez a cortante en el plano del panel

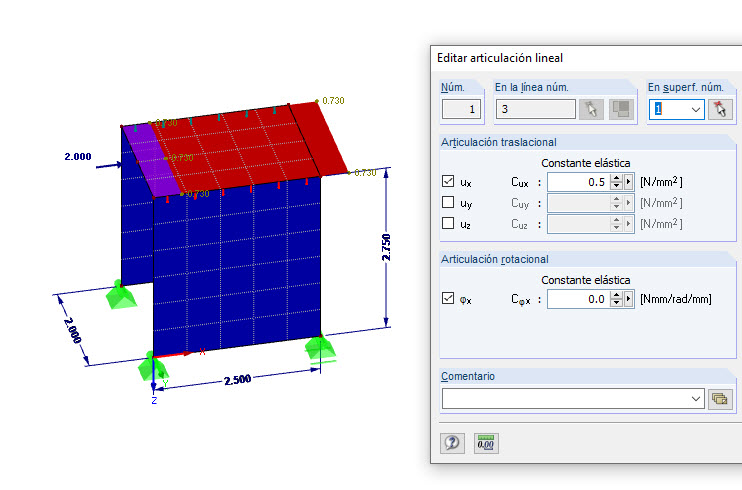
El anclaje de tracción puede definirse directamente en RFEM como un resorte lineal elástico con la rigidez calculada de 6.879,9 N/mm. La comparación de las deformaciones se muestra en la Imagen 1. Las diferencias también pueden seguirse en el modelo adjunto 1.

Para un cálculo tridimensional, este método plantea el problema de la definición de las rigideces de flexión de las placas. Esto se explica en detalle en el artículo técnico mencionado sobre modelos de materiales ortotrópicos.

En lugar de representar la rigidez del panel de madera a través de superficies, se presenta un método para convertir la deformabilidad calculada en una unión de línea.

3 Modelo espacial

La ventaja aquí radica en que las propiedades de la superficie del modelo pueden asumirse como rígidas.

Resumen

En este artículo se mostró el cálculo de un panel de madera a través de una superficie ortotrópica efectiva. El anclaje de tracción puede definirse directamente como una rigidez de resorte. Para un cálculo lineal bidimensional del sistema, los resultados coinciden muy bien con los cálculos manuales en [1]. Se puede realizar un diseño real con las cargas de un cálculo de arriostramiento. El modelo para el cálculo del ejemplo se encuentra en Descargas.

Como otra opción, se mostró la conversión de la deformabilidad en un resorte lineal de la línea. Para modelos espaciales, este método es más adecuado, ya que excluye en gran medida la influencia de la flexión de la placa y la flexión en el plano del panel. También se encuentra el modelo relacionado en Descargas.

En otro artículo se mostrará el arriostramiento de una planta en 2D así como el diseño de los paneles de pared en 3D.