Výpočet panelů na bázi dřeva | 2. Tuhost a poddajnost stěny

Při výpočtu deformace vycházíme z prvního článku této řady.

• KB | Výpočet panelů na bázi dřeva | 1. Stanovení únosnosti a tuhosti

1 Konstrukce

Tuhost stěny

Tuhost stěny vypočítáme při jednotkovém zatížení 1 kN. Další informace o použitých rovnicích najdete v odborné literatuře [1] a také v předchozím příspěvku z této řady.

Příklad použití

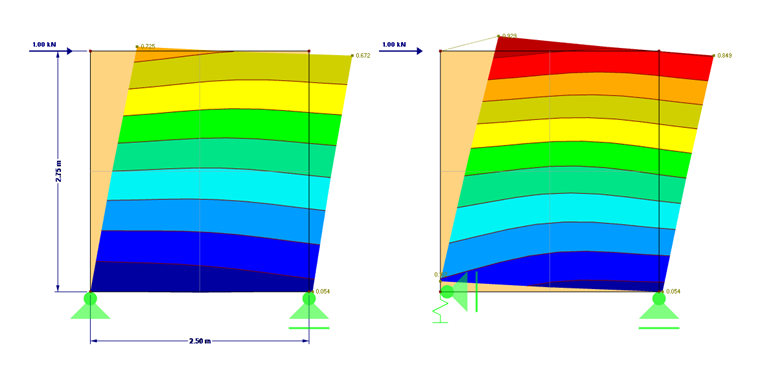
Výpočet tuhosti si ukážeme na jednoduchém příkladu. Rozměry konstrukce jsou znázorněny na obr. 01.

2 Konstrukce

Systém

• Délka stěny l = 2,50 m
• Výška stěny h = 2,75 m
• Stojan C24 6/12 cm, ρm,T = 350 kg/m³
• Opláštění z OSB desek 3, t = 18 mm (na jedné straně), ρm, O = 439 kg/m³, G = 108 kN/cm²
• kser = 159N/mm
• bE = b + t = 12 cm + 1,8 cm = 13,8 cm
• Sponkování d = 1,5 mm, t = 45 mm
• Vzdálenost mezi sponkami av = 60 mm (jedna řada)
• Rastr = 62,5 cm
• Tahová kotva s 10 hřebíky o průměru 4,2 mm
• Velikost sítě konečných prvků je 1,3 m (4 prvky na disk)

Tuhost

• Poddajnost spojovacího prostředku (sevření):
  $${\mathrm{u}}_{\mathrm{k},\mathrm{inst}} = \left(2 · \mathrm{l} + 2 · \mathrm{h}\right) · \frac{{\mathrm{a}}_{\mathrm{v}}}{{\mathrm{k}}_{\mathrm{ser}} · \mathrm{l}²} · \mathrm{F}$$

  $$= \left(2 · 2500 \mathrm{mm} + 2 · 2750 \mathrm{mm}\right) · \frac{60 \mathrm{mm}}{159 \mathrm{N}/\mathrm{mm} · (2500 \mathrm{mm})²} · 1000 \mathrm{N}$$

  $$= 0.634 \mathrm{mm}$$

  Poddajnost spoje (sponky)
• Poddajnost opláštění:
  $${\mathrm{u}}_{\mathrm{G},\mathrm{inst}} = \frac{\mathrm{F} · \mathrm{h}}{{\displaystyle \mathrm{G} · \mathrm{A}}} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm}}{{\displaystyle 1080 \mathrm{N}/\mathrm{mm}² · 18 \mathrm{mm} · 2500 \mathrm{mm}}} = 0.057 \mathrm{mm}$$

  Poddajnost opláštění
• Plastizace žeber:
  $${\mathrm{u}}_{\mathrm{E},\mathrm{inst}} = \frac{2}{3} · \frac{\mathrm{F} · {\mathrm{h}}^3}{\mathrm{E} · \mathrm{A} · {\mathrm{l}}^2} = \frac{2}{3} · \frac{1000 \mathrm{N} ·(2750 \mathrm{mm})³}{11000 \mathrm{N}/\mathrm{mm}² · 60 \mathrm{mm} · 120 \mathrm{mm} · (2500 \mathrm{mm})²} = 0.028 \mathrm{mm}$$

  Poddajnost žeber
• Plastizace kotvy:
  $$\begin{array}{l}{\mathrm{k}}_{\mathrm{ser}} = 10 · {\mathrm{\rho }}_{\mathrm{m}}^{1.5} · \frac{{\mathrm{d}}^{0.8}}{30} = 10 · {(350 \mathrm{kg}/\mathrm{m}³)}^{1.5} · \frac{{(4.2 \mathrm{mm})}^{0.8}}{30} = 6879.9 \mathrm{N}/\mathrm{mm}\\ {\mathrm{u}}_{\mathrm{K},\mathrm{DF}} = \mathrm{h} · \sin \mathrm{\alpha } = 2750 \mathrm{mm} · \sin (0.0195) = 0.94 \mathrm{mm}\\ \mathrm{\alpha } = \frac{\mathrm{F} · \mathrm{h} · 180}{{\mathrm{K}}_{\mathrm{DF}} · \mathrm{\pi }} = \frac{1000 \mathrm{N} · 2750 \mathrm{mm} · 180}{8.06 · {10}^9 · \mathrm{\pi }} = 0.0195°\\ {\mathrm{K}}_{\mathrm{DF}} = \frac{{\mathrm{l}}^2 · {\mathrm{k}}_{\mathrm{ser}}}{2} = \frac{(2500 \mathrm{mm})² · 6879.9 \mathrm{N}/\mathrm{mm}}{2} = 2.15 · {10}^{10}\end{array}$$

  Poddajnost ukotvení
• Součet plastizací (počítáno bez táhla):
  $${\mathrm{u}}_{\mathrm{inst}} = {\mathrm{u}}_{\mathrm{E},\mathrm{inst}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{G},\mathrm{inst}}}}} \frac{1}{\sum {\displaystyle \frac{1}{{\mathrm{u}}_{\mathrm{k},\mathrm{inst}}}}} = 0.028 0.07 0.63 = 0.728 \mathrm{mm}$$

  Součet skluzů

Přepočet na účinnou plochu

Vypočítaná tuhost se přepočte na účinnou ortotropní tuhost stěny. Základní informace o ortotropním materiálovém modelu lze najít v tomto příspěvku.

• KB | Ortotropní materiálové modely

• Normálová složka tuhosti:
  $$\begin{array}{l}{\mathrm{E}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}³}{{3 · \mathrm{u}}_{\mathrm{E},\mathrm{inst}} · {\displaystyle \frac{\mathrm{l}³ · \mathrm{b}}{12}}}=\frac{1 \mathrm{kN} · (275 \mathrm{cm})³}{3 · 0.0028 \mathrm{cm} · {\displaystyle \frac{(250 \mathrm{cm})³ · 12 \mathrm{cm}}{12}}} = 158.45 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}66/77 = \frac{\mathrm{E} · \mathrm{d}}{1 - \mathrm{\nu }} = 158.45 \mathrm{kN}/\mathrm{cm}² · 12 \mathrm{cm} = 1901.4 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Složka osové tuhosti
• Smyková tuhost v rovině stěny:
  $$\begin{array}{l}{\mathrm{G}}_{\mathrm{eq}} = \frac{\mathrm{F} · \mathrm{h}}{({\mathrm{u}}_{\mathrm{G},\mathrm{inst}} {\mathrm{u}}_{\mathrm{k},\mathrm{inst}}) · {\displaystyle \frac{5}{6}} · {\mathrm{b}}_{\mathrm{E}} · \mathrm{l}} = \frac{1 \mathrm{kN} · 275 \mathrm{cm}}{0.07 \mathrm{cm} · {\displaystyle \frac{5}{6}} · 13.8 \mathrm{cm} · 250 \mathrm{cm}} = 1.37 \mathrm{kN}/\mathrm{cm}²\\ \mathrm{D}88 = {\mathrm{G}}_{\mathrm{eq}} · {\mathrm{b}}_{\mathrm{E}} = 1.37 \mathrm{kN}/\mathrm{cm}² · 13.8 \mathrm{cm} = 18.86 \mathrm{kN}/\mathrm{cm}\end{array}$$

  Tuhost ve smyku v rovině stěny

Tahovou kotvu lze zadat přímo v programu RFEM jako lineární pružinu s vypočtenou tuhostí 6 879,9 N/mm. Na obr. 01 vidíme porovnání deformací. Rozdíly jsou zdokumentovány také v připojeném modelu 1.

Při 3D výpočtu s sebou tato metoda přináší problém se zadáním tuhosti desky v ohybu. Ve výše zmíněném příspěvku o ortotropních materiálových modelech najdeme podrobnější vysvětlení.

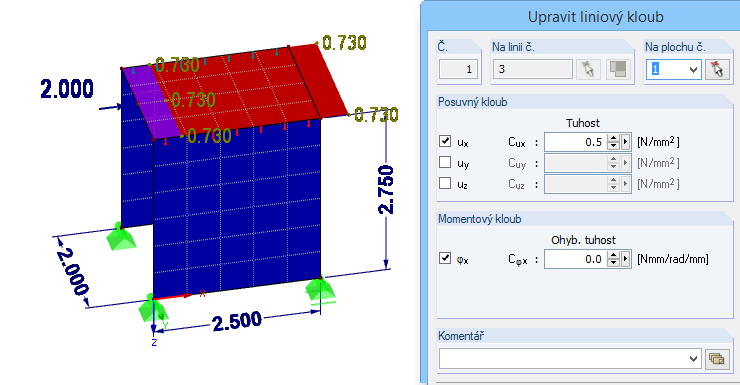
Místo modelování tuhosti panelů na bázi dřeva pomocí ploch se dále podíváme na metodu přepočtu stanovené poddajnosti na liniový kloub.

3 Prostorový model

Výhodou je, že v tomto případě lze plochy v modelu uvažovat jako tuhé.

Závěr a výhled

V našem příspěvku jsme ukázali, jak lze vypočítat panel na bázi dřeva pomocí účinné ortotropní plochy. Tahovou kotvu lze zadat přímo jako tuhost pružiny. Pro lineární dvourozměrný výpočet systému výsledky velmi dobře odpovídají ručním výpočtům v [1]. Lze tak provést reálný výpočet se zatížením z posouzení výztuže. Model, který jsme použili pro náš příklad, je k dispozici ke stažení pod tímto článkem.

Jako další možnost jsme si ukázali přepočet poddajnosti na lineární pružinu linie. Tato metoda bývá pro prostorové modely vhodnější, protože do značné míry vylučuje vliv ohybu stěny i ohybu v rovině stěny. Příslušný model si lze také stáhnout v sekci Ke stažení pod tímto článkem.

V našem příštím příspěvku se budeme zabývat vyztužením v půdorysu ve 2D a posouzením stěnových panelů ve 3D.