![Разветвленная балка с распределенной нагрузкой (Источник: [3])](/ru/webimage/009690/467522/01-de-png.png)
В этих опорах вилки возникают крутящие моменты, которые необходимо проверять в соответствии с [2] , раздел 6.1.9:
Суперпозиция внутренних сил от сдвига и кручения должна предотвратить появление трещин на жесткой опоре.
![Трещины на клееной балке (Источник: [4])](/ru/webimage/009691/467524/02-de-png.png)
Крутящий момент на концевых опорах возникает из-за прогиба балки в случае синусоидальной нагрузки (см. Рисунок 03).
Согласно [1] , для прекамбера должно быть установлено значение l/400. Это основано на минимальных требованиях к усилению вторичной опорной системы. Более подробную информацию можно найти, например, в [3].
Однако современные методы расчета стержней не позволяют обнаружить кручение на опорах. Кроме того, многие программы расчета не учитывают деформацию сечения. Поскольку расчет часто выполняется в программах расчета двухмерных конструкций из каркаса, ограничивающий критерий приведен в [2], раздел NCI до 9.2.5.3 (выражение 2):
Если коэффициент гибкости балки ниже этого значения, компонентами напряжения кручения можно пренебречь.
Расчет в клееной древесине RX-TIMBER
Следующий пример поясняет эту связь.
Конструкция:
Пролет = 25 м
Материал = GL24c
Сечение = 12 см/242 см (без конькового клина)
Балка подвергается равномерно распределенной нагрузке 13,5 кН/м. Собственный вес не учитывается.
Основным расчетом является расчет на кручение, указанный в Выражении 1. В этом случае длинапролета равна 2,46 м. Расстояние между опорами при продольном изгибе при кручении может применяться только в том случае, если горизонтальная жесткость вспомогательной опорной системы составляет <l/500 или l/1000. Здесь это не применяется.
Внутренние силы и напряжения:
Расчет с учетом кручения при деформации
RF-/FE-LTB позволяет приложить к балке эксцентрическую сжимающую силу. Таким образом, линейная нагрузка 13,5 кН/м может быть приложена не по центру балки.
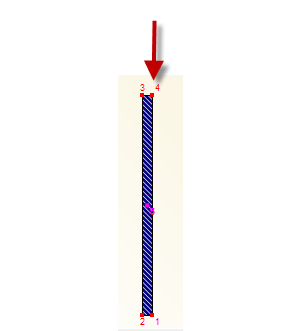
Как показано на рисунке 05, эксцентриситет груза установлен на 6 см. Кроме того, применяется боковая деформация 6,15 см в соответствии с [2] (NA.5).
Основываясь на теории изгиба Бернулли, RF‑/FE ‑ LTB может определить критическую нагрузку Fki и, следовательно, идеальный упругий критический момент Mki и нагрузку потери устойчивости Nki, phi.
Расчет основан на теории потери устойчивости второго порядка. Также учитывается перекос сечения (7-я степень свободы).
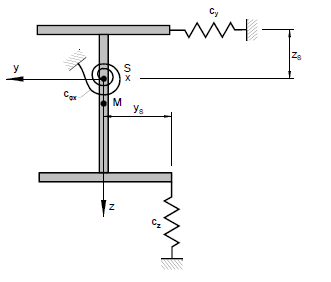
Чтобы учесть соответствующее покрытие крыши или усиление за счет вторичной опорной системы, определяется пружина вращения вокруг локальной оси x элемента. Программа преобразует эту пружину в центр сдвига M.
Применяется только пружина кручения, чтобы получить величину деформации, показанную на рисунке 2. Поступательная пружина на верхнем фланце конструкции была бы ближе к реальности. Однако из-за кривизны балки невозможно создать требуемую форму несовершенства. Затем фигура несовершенства будет прорезана в середине, как показано на рисунке 7. Таким образом, крутящие моменты будут значительно уменьшены.
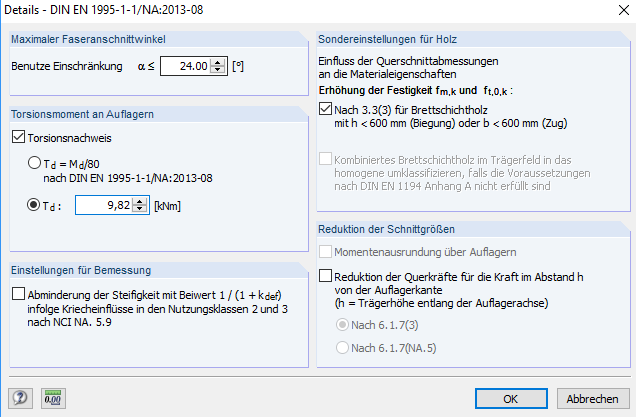
При ограничении вращения 500 кНм/м на опорах возникает крутящий момент 9,8 кНм.
Используя этот крутящий момент, можно снова выполнить расчет по [1] на клееной балке RX-TIMBER. Для этого определенный крутящий момент определяется в RX-TIMBER Glued-Laminated Beam.
Заключение
Конструкцию можно спроектировать гораздо более экономично, учитывая жесткость поперечного сечения на изгиб.
Отличие от общего подхода, описанного в разделе 9.2.5 в [2], становится еще более серьезным при замене виртуального ограничения вращения на поступательную жесткость пружины 915 Н/мм для продольной деформации обычного гвоздя в соединительном элементе, например .
![Разветвленная балка с распределенной нагрузкой (Источник: [3])](/ru/webimage/009690/467522/01-de-png.png?mw=512&hash=2551750327252c0e49d549ec0d9fb2579bfaa885)
![Разветвленная балка с распределенной нагрузкой (Источник: [3])](/ru/webimage/009690/467522/01-de-png.png?mw=350&hash=d9822b6f398f12dfbe5ade0e1b85cf57c27573ab)
![Трещины на клееной балке (Источник: [4])](/ru/webimage/009691/467524/02-de-png.png?mw=350&hash=a41f4e52dba9540e3cac9285b98e8f925c1beb4e)
.png?mw=512&hash=4e74affa9ad0c7b703151c5085ac9b8e59171c23)
.JPG?mw=350&hash=354dcaeb798219977d00c1979f12a0628654c9f0)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)