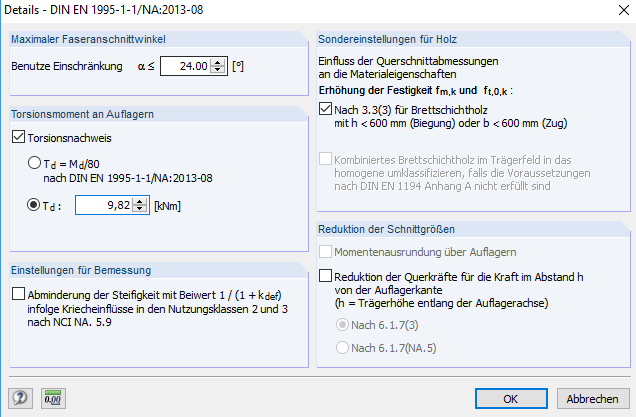
U těchto ložisek vidlice vznikají krouticí momenty, které je třeba ověřit podle [2], odstavec 6.1.9:
Superpozice vnitřních sil od smykové síly a kroucení by měla zabránit vzniku trhlin na tuhé podpoře.
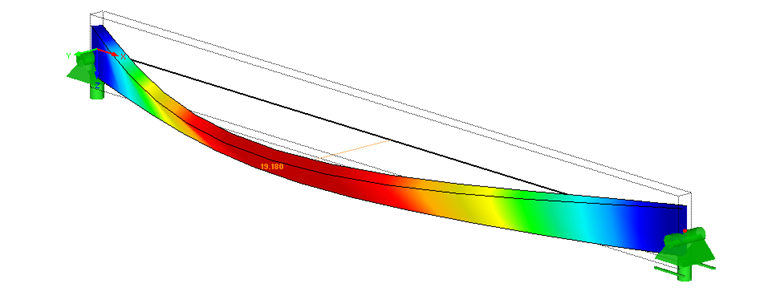
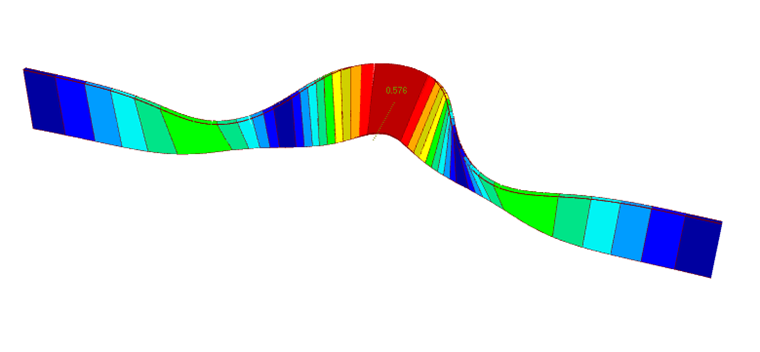
Krouticí moment na koncových podporách je způsoben průhybem nosníku v případě sinusového zatížení (viz obr. 03).
Podle [1] se má pro počáteční prohnutí nastavit hodnota l/400. Vychází se přitom z minimálního požadavku na vyztužení sekundárního nosného systému. Další informace lze například najít v [3].
Současné statické metody posouzení prutů ovšem nedokáží zaznamenat kroucení na podporách. Mnoho výpočetních programů navíc neumožňuje zohlednit deplanaci průřezu. Vzhledem k tomu, že výpočet se často provádí v 2D programech prutových konstrukcí, stanoví se v [2], odstavec NCI k 9.2.5.3 (výraz 2) toto omezující kritérium:
Pokud je štíhlostní poměr nosníku pod touto hodnotou, lze složky napětí v kroucení zanedbat.
Výpočet v programu RX-TIMBER Glued-Laminated Timber
Následující příklad objasňuje tento vztah.
Konstrukce:
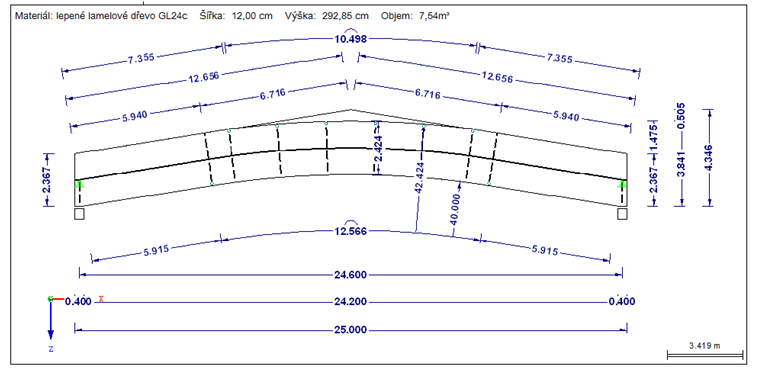
Rozpětí = 25 m
Materiál = GL24c
Průřez = 12 cm/242 cm (bez hřebenového klínu)
Na nosník působí rovnoměrné zatížení 13,5 kN/m. Vlastní tíhu zanedbáme.
Rozhodujícím posouzením je posouzení napětí v kroucení podle výrazu 1. V tomto případě je hodnota lef stejná jako délka pole 2,46 m. Vzdálenost podpor pro klopení lze použít pouze v případě, že vodorovné vyztužení sekundárního nosného systému je <l/500 nebo l/1,000. Zde se toto nepoužije.
Vnitřní síly a napětí:
Výpočet se zohledněním vázaného kroucení
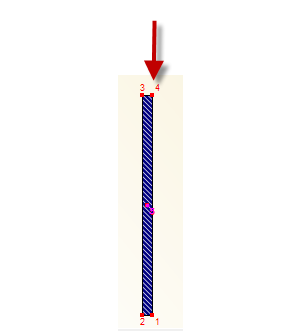
V modulu RF-/FE-LTB lze na nosník aplikovat excentrickou tlakovou sílu. Zatížení na linii 13,5 kN/m tak může působit excentricky od nosníku.
Jak je znázorněno na obr. 05, excentricita zatížení je 6 cm. Dále se uvažuje boční deformace 6,15 cm podle [2] (NP.5).
Na základě Bernoulliho teorie ohybu může přídavný modul RF-/FE ‑ LTB stanovit kritickou sílu Fki a tím i pružný kritický moment Mki a kritickou sílu Nki, phi.
Při výpočtu se vychází z teorie klopení druhého řádu. Zohledňuje se také deplanace průřezu (7. stupeň volnosti).
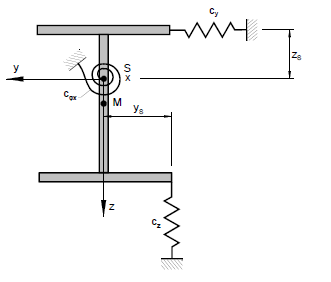
Pro zohlednění příslušné střešní krytiny nebo výztuže v důsledku přídavného nosného systému se zadá rotační pružina okolo lokální osy x prutu. Program tuto pružinu přepočítá na střed smyku M.
K dosažení deformačního tvaru podle obr. 2 se použije pouze torzní pružina. Translační pružina na horní pásnici konstrukce by odpovídala skutečnosti. Požadovaný tvar imperfekce však nemůže být vytvořen z důvodu zakřivení nosníku. Tvar imperfekce by pak uprostřed prořízl, jak je znázorněno na obrázku 7. Tímto způsobem by se výrazně snížily krouticí momenty.
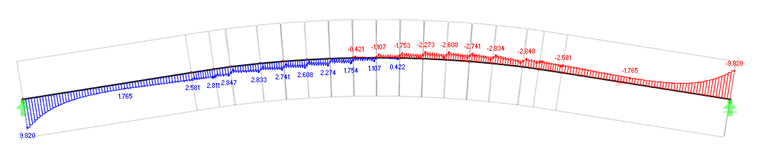
Při torzním uložení 500 kNm/m vznikají na podporách krouticí momenty 9,8 kNm.
Na základě tohoto krouticího momentu lze posouzení [1] provést znovu v programu RX-TIMBER Glued-Laminated Beam. Za tímto účelem se stanoví stanovený krouticí moment v lepeném lamelovém nosníku RX-TIMBER.
Závěr
Konstrukci lze navrhnout mnohem hospodárněji, pokud se zohlední deplanační tuhost průřezu.
Rozdíl oproti obecnému přístupu z odstavce 9.2.5 v [2] je ještě výraznější, pokud například nahradíme virtuální torzní uložení translační tuhostí 915 N/mm pro podélnou deformaci běžného hřebíku ve spojovacím prutu. .
![Vidlicový nosník s rozděleným zatížením (Zdroj: [3])](/cs/webimage/009690/467522/01-de-png.png)
![Trhliny na Glulam Beams (Zdroj: [4])](/cs/webimage/009691/467524/02-de-png.png)