![Belka rozwidlona z rozproszonym obciążeniem (Źródło: [3])](/pl/webimage/009690/467522/01-de-png.png)
Na łożyskach widełkowych występują momenty skręcające, które należy zweryfikować zgodnie z [2] sekcja 6.1.9:
Superpozycja sił wewnętrznych od siły tnącej i skręcania powinna zapobiegać pęknięciom sztywnej podpory.
![Pęknięcia na belkach z drewna klejonego warstwowo (Źródło: [4])](/pl/webimage/009691/467524/02-de-png.png)
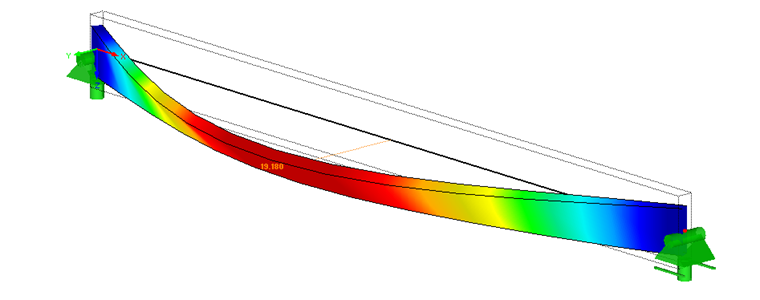
Moment skręcający na podporach końcowych jest spowodowany ugięciem belki w przypadku obciążenia o kształcie sinusoidalnym (por. Rysunek 03).
Zgodnie z [1] wartość l/400 należy ustawić dla komory wstępnej. Jest to oparte na minimalnym wymaganiu usztywnienia drugorzędnego układu podporowego. Więcej informacji można znaleźć np. w [3].
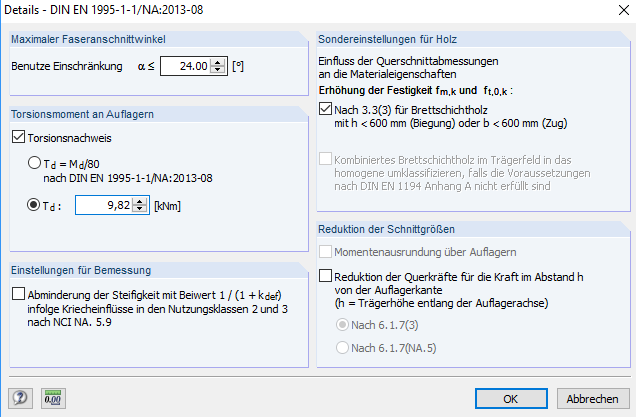
Jednak obecne metody analizy prętów konstrukcyjnych nie umożliwiają wykrywania skręcania na podporach. Ponadto wiele programów obliczeniowych nie pozwala na uwzględnienie spaczenia przekroju. Ponieważ obliczenia są często przeprowadzane w programach 2D do analizy statyczno-wytrzymałościowej konstrukcji szkieletowej, kryterium ograniczające podano w [2], sekcja NCI do 9.2.5.3 (Wyrażenie 2):
Jeżeli smukłość belki jest niższa od tej wartości, składowe naprężenia skręcającego można pominąć.
Obliczenia w drewnie klejonym RX-TIMBER
Poniższy przykład wyjaśnia tę relację.
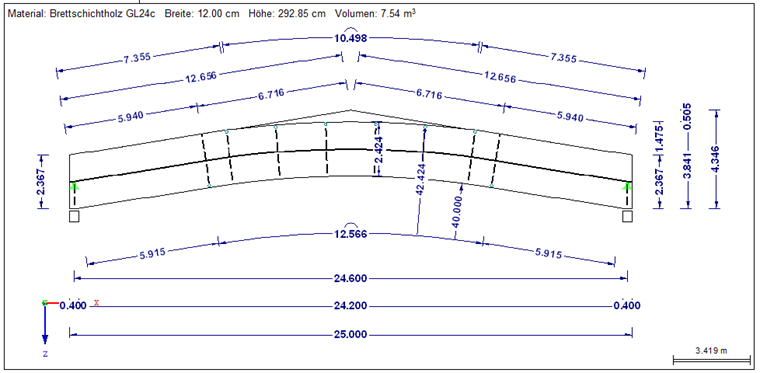
Konstrukcja:
Rozpiętość = 25 m
Materiał = GL24c
Przekrój = 12 cm/242 cm (bez kalenicy)
Belka jest poddawana obciążeniu równomiernie rozłożonemu 13,5 kN/m. Ciężar własny jest pomijany.
Podstawowym kryterium obliczeniowym jest analiza naprężeń skręcających określona w wyrażeniu 1. W tym przypadku lef jest równe rozpiętości przęsła 2,46 m. Rozstaw podpór dla zwichrzenia może być zastosowany tylko wtedy, gdy poziome usztywnienie drugorzędnego układu podporowego wynosi < l/500 lub l/1000. Nie ma to tutaj zastosowania.
Siły wewnętrzne i naprężenia:
Obliczenia z uwzględnieniem skręcania skrępowanego
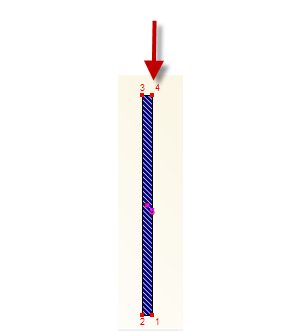
RF-/FE-LTB umożliwia przyłożenie do belki mimośrodowej siły ściskającej. Dzięki temu obciążenie liniowe 13,5 kN/m może zostać przyłożone poza środkiem belki.
Jak pokazano na rysunku 05, mimośród obciążenia jest ustawiony na 6 cm. Ponadto zastosowano odkształcenie boczne 6,15 cm zgodnie z [2] (NA.5).
W oparciu o teorię zginania Bernoulliego, moduł RF-/FE-LTB może wyznaczyć obciążenie krytyczne Fki , a tym samym idealny sprężysty moment krytyczny Mki oraz obciążenie wyboczeniowe Nki,phi.
Obliczenia oparte są na teorii wyboczenia skrętnego drugiego rzędu. Uwzględniane jest również spaczenie przekroju (7 stopień swobody).
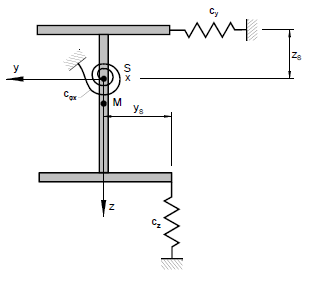
Aby uwzględnić odpowiednie pokrycie dachu lub usztywnienie ze względu na drugorzędny układ podporowy, zdefiniowana jest sprężystość obrotowa wokół lokalnej osi x pręta. Program przekształca tę sprężynę w środek ścinania M.
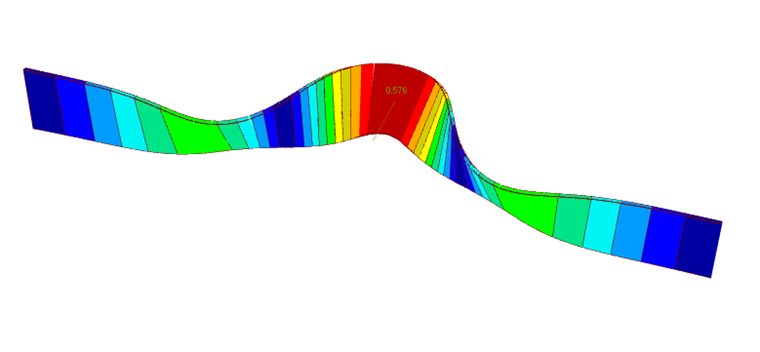
W celu uzyskania odkształcenia pokazanego na rysunku 2 zastosowano tylko sprężynę skrętową. Sprężyna translacyjna na górnej półce konstrukcji byłaby bliższa rzeczywistości. Wymagany kształt imperfekcji nie może zostać utworzony ze względu na krzywiznę belki. Figura imperfekcji przecinałaby wówczas środek, jak pokazano na rysunku 7. W ten sposób momenty skręcające zostałyby znacznie zredukowane.
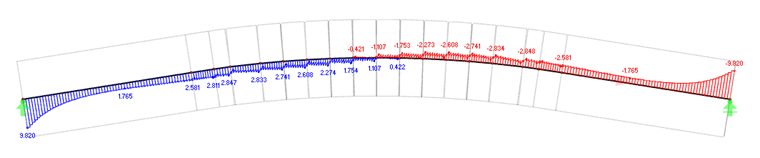
Przy skrępowaniu wynoszącym 500 kNm/m na podporach powstają momenty skręcające o wartości 9,8 kNm.
Wykorzystując ten moment skręcający, można ponownie przeprowadzić obliczenia według [1] w module RX-TIMBER Glued-Laminated Beam. W tym celu w RX-TIMBER Glued-Laminated Beam definiowany jest moment skręcający.
Uwagi końcowe
Konstrukcję można zaprojektować znacznie bardziej ekonomicznie, biorąc pod uwagę sztywność skrępowania przekroju.
Różnica w stosunku do podejścia ogólnego z rozdziału 9.2.5 in [2] jest jeszcze bardziej poważna, gdy dla odkształcenia podłużnego zwykłego gwoździa w elemencie sprzęgającym zastąpiono rzeczywiste ograniczenie obrotu translacyjną sztywnością sprężystą równą 915 N/mm .