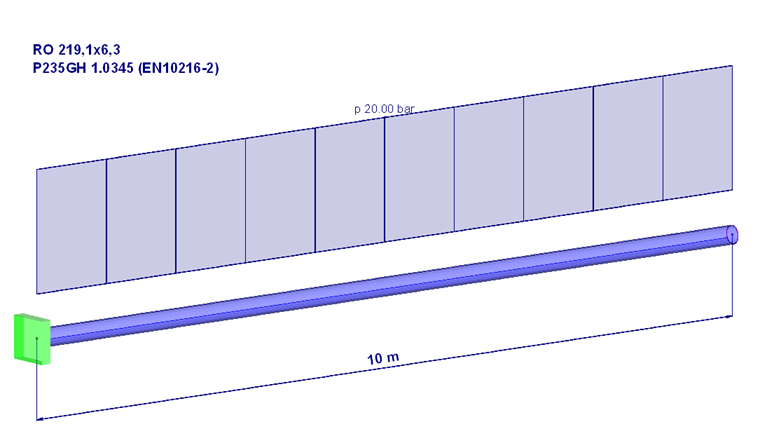
Для лучшего понимания используется следующий пример.
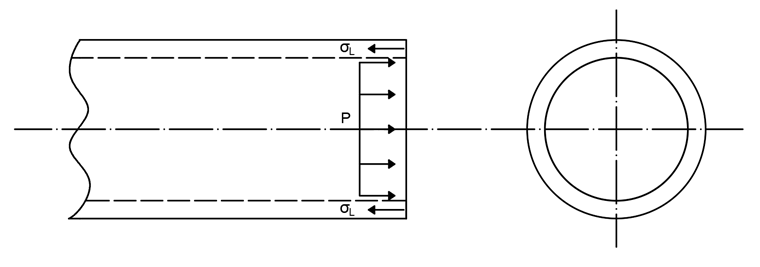
Труба считается закрытой с обеих сторон. С одной стороны, давление действует перпендикулярно внутренней «площади поверхности внешней накладки».
Возникающая таким образом сила должна быть поглощена стенкой трубы. Это приводит к продольному напряжению, которое может быть рассчитано следующим образом:
где
ri, re = внутренний и внешний радиус
С другой стороны, внутреннее давление действует перпендикулярно площади поверхности стенки трубы. Это приводит к касательному, а также радиальному напряжению, которое можно определить по следующим формулам:
где
r = радиус в пределах ri ≤ r ≤ re
Видно, что напряжения зависят от рассматриваемого радиуса r. Это, наоборот, означает, что они проходят неравномерно в поперечном сечении. Однако для тонкостенных труб (внешний диаметр/внутренний диаметр <1,2) можно предположить равномерное распределение напряжений. Таким образом, среднее касательное и радиальное напряжение равно:
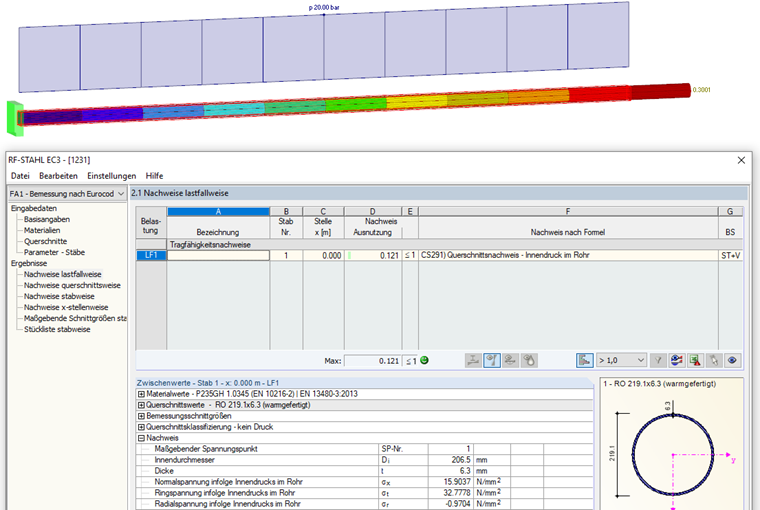
Поставив начальные значения в формулы, мы получим следующие напряжения:
Изменение длины трубы также является результатом внутреннего давления. В общем, изменение длины равно произведению длины на деформацию эпсилон:
ΔL = L ∙ ε
Деформация трубы происходит от трех вычисленных выше напряжений:
Таким образом, изменение в длине равно:
ΔL = 10 000 мм ∙ 3 ∙ 10-5 = 0.3 мм
Результаты, рассчитанные вручную в данной статье, могут быть воспроизведены в RFEM (деформация) или в модулях для расчета стальных конструкций (напряжения).
В расчете деформации важно активировать эффект Бурдона в общих параметрах расчета в RFEM. Если вы хотите учесть не только осевую деформацию труб, но и растяжение отводов, примените дополнительный модуль RF-PIPING.
Литература